Energy-based physics-informed neural network for frictionless contact problems under large deformation

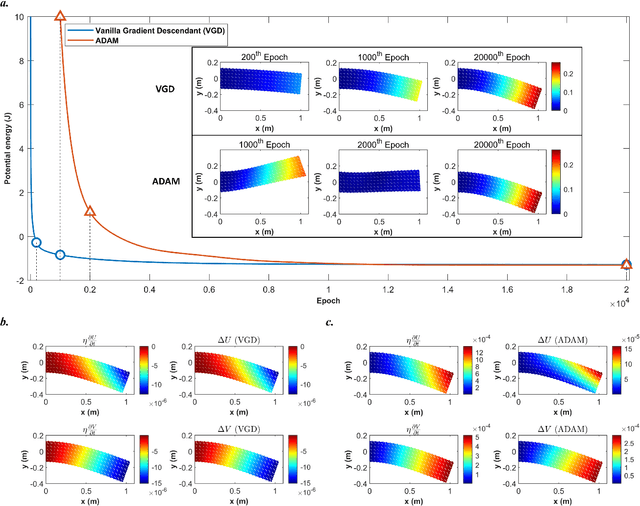
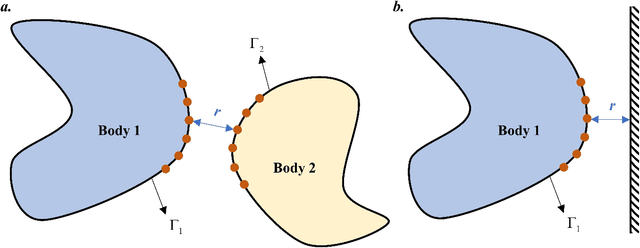
Numerical methods for contact mechanics are of great importance in engineering applications, enabling the prediction and analysis of complex surface interactions under various conditions. In this work, we propose an energy-based physics-informed neural network (PINNs) framework for solving frictionless contact problems under large deformation. Inspired by microscopic Lennard-Jones potential, a surface contact energy is used to describe the contact phenomena. To ensure the robustness of the proposed PINN framework, relaxation, gradual loading and output scaling techniques are introduced. In the numerical examples, the well-known Hertz contact benchmark problem is conducted, demonstrating the effectiveness and robustness of the proposed PINNs framework. Moreover, challenging contact problems with the consideration of geometrical and material nonlinearities are tested. It has been shown that the proposed PINNs framework provides a reliable and powerful tool for nonlinear contact mechanics. More importantly, the proposed PINNs framework exhibits competitive computational efficiency to the commercial FEM software when dealing with those complex contact problems. The codes used in this manuscript are available at https://github.com/JinshuaiBai/energy_PINN_Contact.(The code will be available after acceptance)

DeepNetBeam: A Framework for the Analysis of Functionally Graded Porous Beams

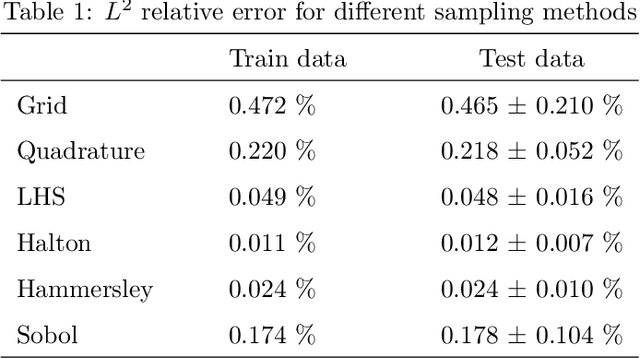
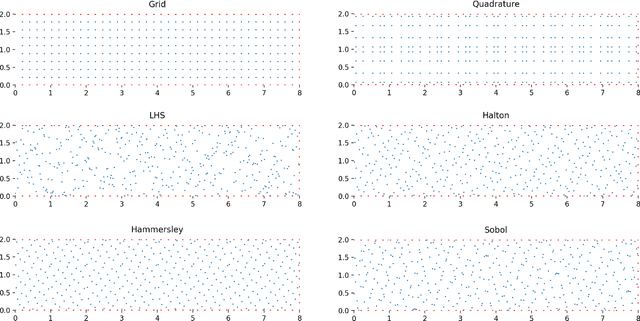
This study investigates different Scientific Machine Learning (SciML) approaches for the analysis of functionally graded (FG) porous beams and compares them under a new framework. The beam material properties are assumed to vary as an arbitrary continuous function. The methods consider the output of a neural network/operator as an approximation to the displacement fields and derive the equations governing beam behavior based on the continuum formulation. The methods are implemented in the framework and formulated by three approaches: (a) the vector approach leads to a Physics-Informed Neural Network (PINN), (b) the energy approach brings about the Deep Energy Method (DEM), and (c) the data-driven approach, which results in a class of Neural Operator methods. Finally, a neural operator has been trained to predict the response of the porous beam with functionally graded material under any porosity distribution pattern and any arbitrary traction condition. The results are validated with analytical and numerical reference solutions. The data and code accompanying this manuscript will be publicly available at https://github.com/eshaghi-ms/DeepNetBeam.

Kolmogorov Arnold Informed neural network: A physics-informed deep learning framework for solving PDEs based on Kolmogorov Arnold Networks

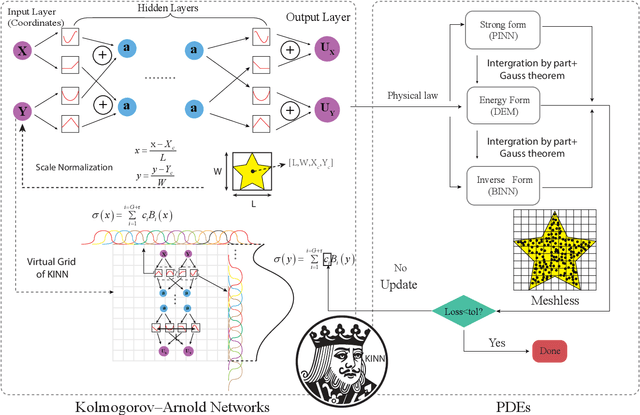
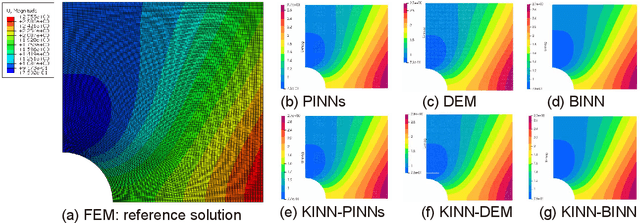
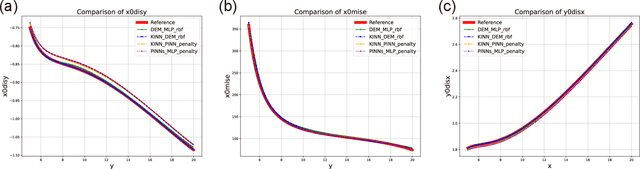
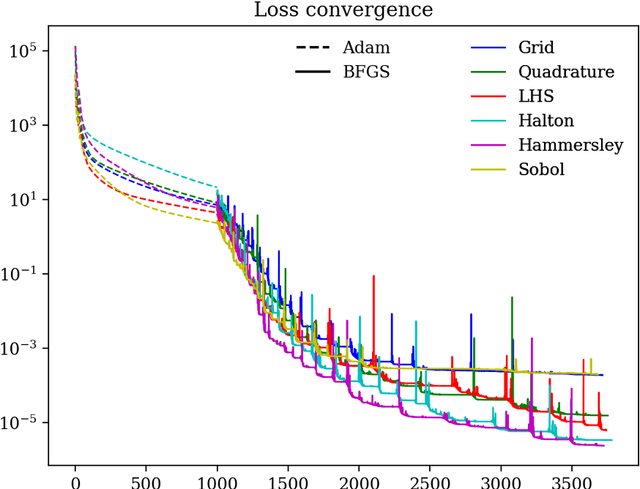
AI for partial differential equations (PDEs) has garnered significant attention, particularly with the emergence of Physics-informed neural networks (PINNs). The recent advent of Kolmogorov-Arnold Network (KAN) indicates that there is potential to revisit and enhance the previously MLP-based PINNs. Compared to MLPs, KANs offer interpretability and require fewer parameters. PDEs can be described in various forms, such as strong form, energy form, and inverse form. While mathematically equivalent, these forms are not computationally equivalent, making the exploration of different PDE formulations significant in computational physics. Thus, we propose different PDE forms based on KAN instead of MLP, termed Kolmogorov-Arnold-Informed Neural Network (KINN). We systematically compare MLP and KAN in various numerical examples of PDEs, including multi-scale, singularity, stress concentration, nonlinear hyperelasticity, heterogeneous, and complex geometry problems. Our results demonstrate that KINN significantly outperforms MLP in terms of accuracy and convergence speed for numerous PDEs in computational solid mechanics, except for the complex geometry problem. This highlights KINN's potential for more efficient and accurate PDE solutions in AI for PDEs.

Multigoal-oriented dual-weighted-residual error estimation using deep neural networks

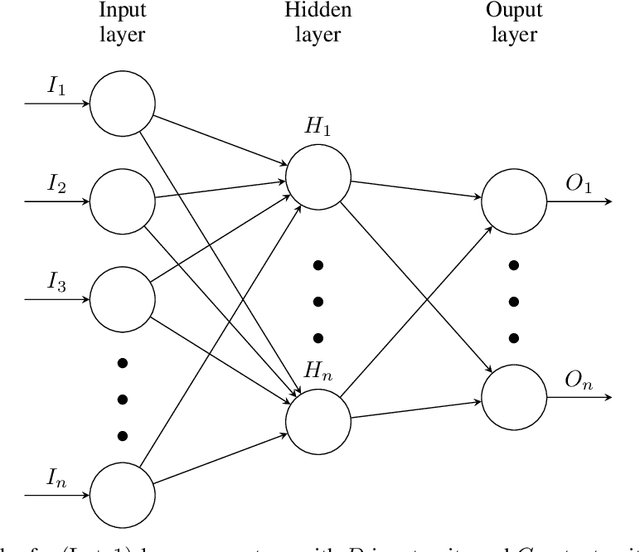
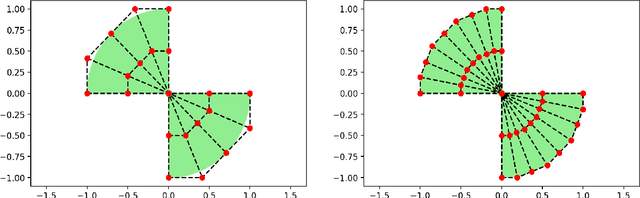
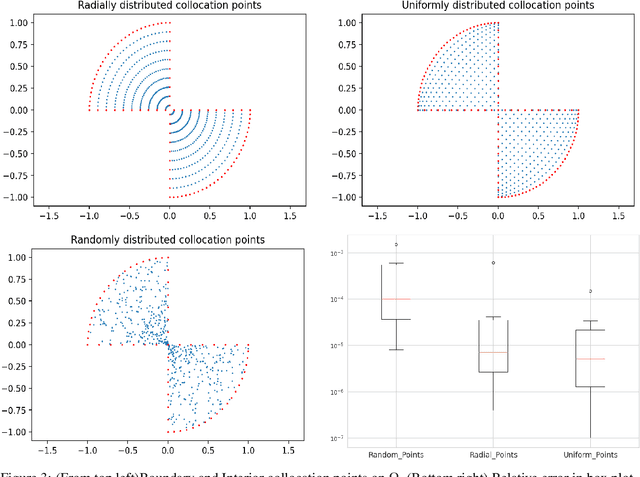
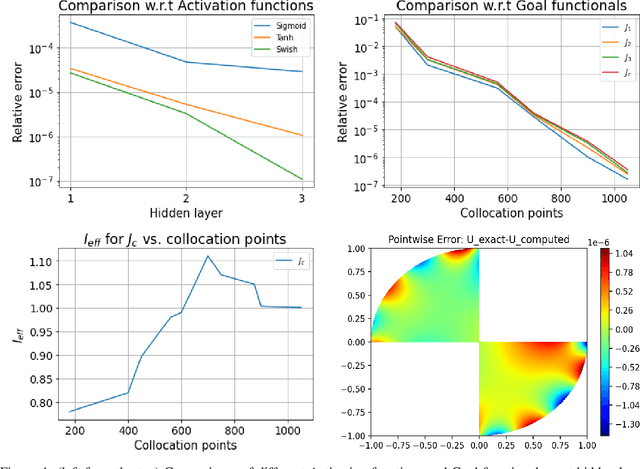
Deep learning has shown successful application in visual recognition and certain artificial intelligence tasks. Deep learning is also considered as a powerful tool with high flexibility to approximate functions. In the present work, functions with desired properties are devised to approximate the solutions of PDEs. Our approach is based on a posteriori error estimation in which the adjoint problem is solved for the error localization to formulate an error estimator within the framework of neural network. An efficient and easy to implement algorithm is developed to obtain a posteriori error estimate for multiple goal functionals by employing the dual-weighted residual approach, which is followed by the computation of both primal and adjoint solutions using the neural network. The present study shows that such a data-driven model based learning has superior approximation of quantities of interest even with relatively less training data. The novel algorithmic developments are substantiated with numerical test examples. The advantages of using deep neural network over the shallow neural network are demonstrated and the convergence enhancing techniques are also presented

Resistance-Time Co-Modulated PointNet for Temporal Super-Resolution Simulation of Blood Vessel Flows

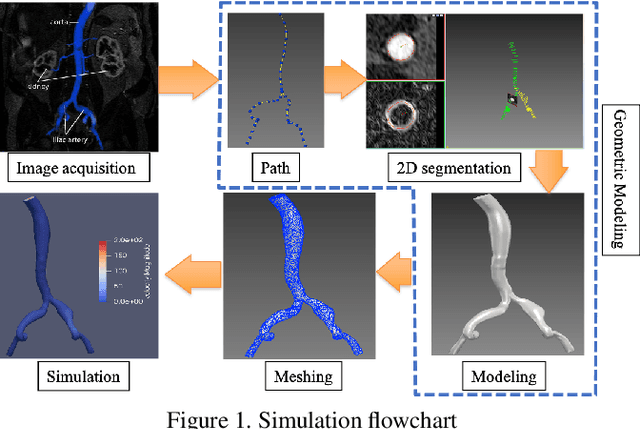
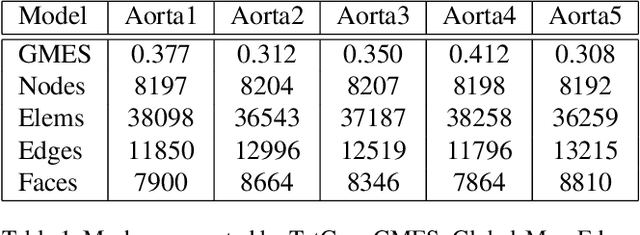
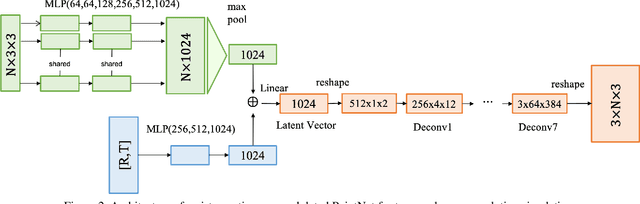
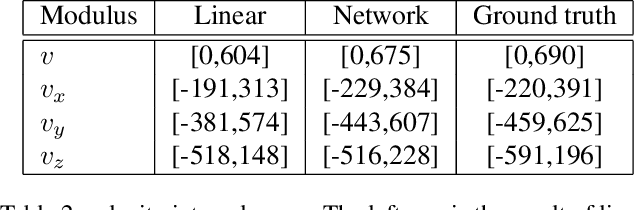
In this paper, a novel deep learning framework is proposed for temporal super-resolution simulation of blood vessel flows, in which a high-temporal-resolution time-varying blood vessel flow simulation is generated from a low-temporal-resolution flow simulation result. In our framework, point-cloud is used to represent the complex blood vessel model, resistance-time aided PointNet model is proposed for extracting the time-space features of the time-varying flow field, and finally we can reconstruct the high-accuracy and high-resolution flow field through the Decoder module. In particular, the amplitude loss and the orientation loss of the velocity are proposed from the vector characteristics of the velocity. And the combination of these two metrics constitutes the final loss function for network training. Several examples are given to illustrate the effective and efficiency of the proposed framework for temporal super-resolution simulation of blood vessel flows.

A Deep Collocation Method for the Bending Analysis of Kirchhoff Plate

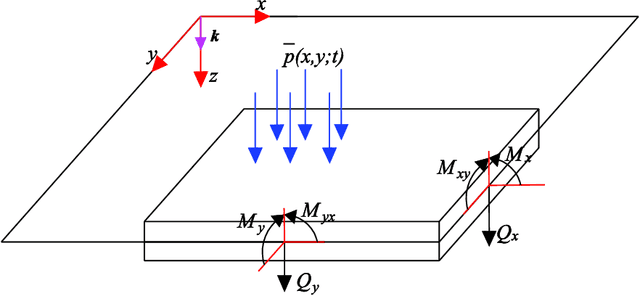
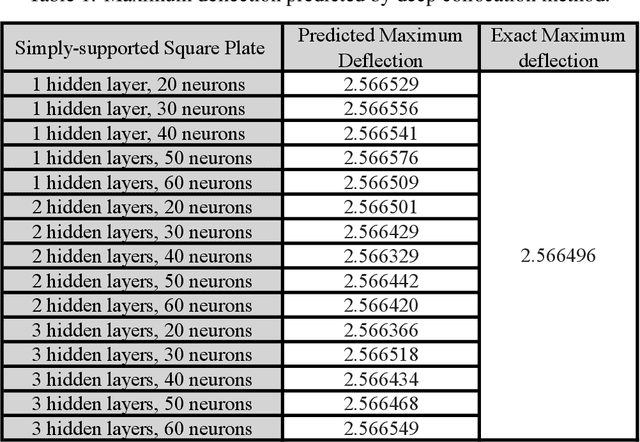
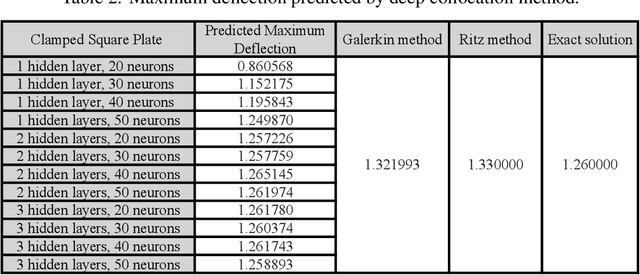
In this paper, a deep collocation method (DCM) for thin plate bending problems is proposed. This method takes advantage of computational graphs and backpropagation algorithms involved in deep learning. Besides, the proposed DCM is based on a feedforward deep neural network (DNN) and differs from most previous applications of deep learning for mechanical problems. First, batches of randomly distributed collocation points are initially generated inside the domain and along the boundaries. A loss function is built with the aim that the governing partial differential equations (PDEs) of Kirchhoff plate bending problems, and the boundary/initial conditions are minimised at those collocation points. A combination of optimizers is adopted in the backpropagation process to minimize the loss function so as to obtain the optimal hyperparameters. In Kirchhoff plate bending problems, the C1 continuity requirement poses significant difficulties in traditional mesh-based methods. This can be solved by the proposed DCM, which uses a deep neural network to approximate the continuous transversal deflection, and is proved to be suitable to the bending analysis of Kirchhoff plate of various geometries.

Deep Autoencoder based Energy Method for the Bending, Vibration, and Buckling Analysis of Kirchhoff Plates

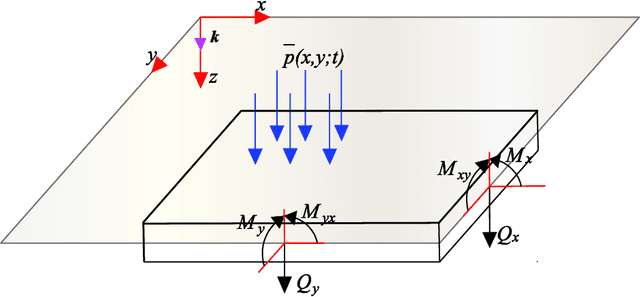
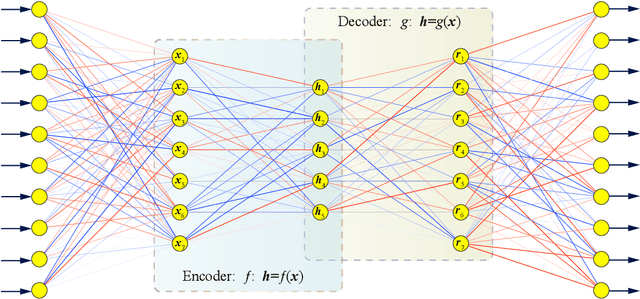
In this paper, we present a deep autoencoder based energy method (DAEM) for the bending, vibration and buckling analysis of Kirchhoff plates. The DAEM exploits the higher order continuity of the DAEM and integrates a deep autoencoder and the minimum total potential principle in one framework yielding an unsupervised feature learning method. The DAEM is a specific type of feedforward deep neural network (DNN) and can also serve as function approximator. With robust feature extraction capacity, the DAEM can more efficiently identify patterns behind the whole energy system, such as the field variables, natural frequency and critical buckling load factor studied in this paper. The objective function is to minimize the total potential energy. The DAEM performs unsupervised learning based on random generated points inside the physical domain so that the total potential energy is minimized at all points. For vibration and buckling analysis, the loss function is constructed based on Rayleigh's principle and the fundamental frequency and the critical buckling load is extracted. A scaled hyperbolic tangent activation function for the underlying mechanical model is presented which meets the continuity requirement and alleviates the gradient vanishing/explosive problems under bending analysis. The DAEM can be easily implemented and we employed the Pytorch library and the LBFGS optimizer. A comprehensive study of the DAEM configuration is performed for several numerical examples with various geometries, load conditions, and boundary conditions.

Analysis of three dimensional potential problems in non-homogeneous media with deep learning based collocation method

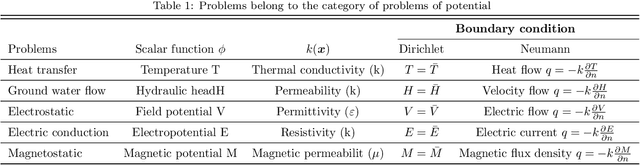
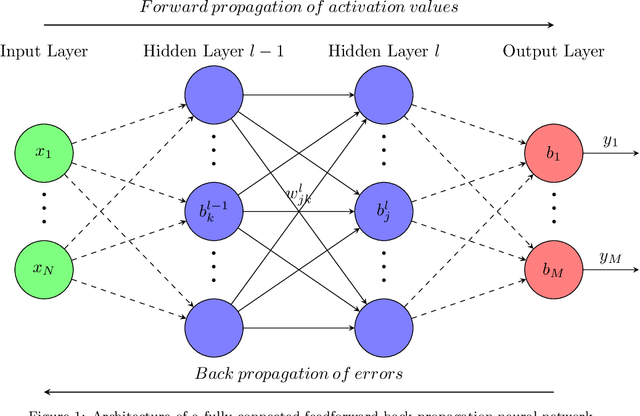
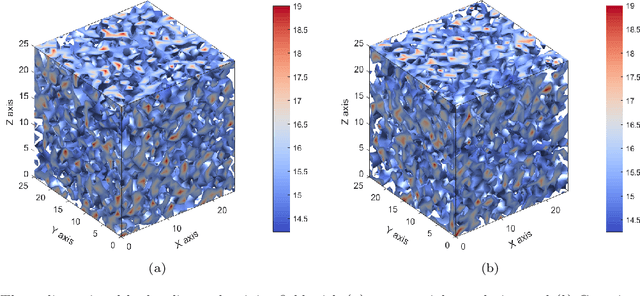
A deep learning based collocation method is presented in this paper to solve the three dimensional potential problems in non-homogeneous media. Based on the universal approximation theorem, the neural network can be utilized to approximate solutions for different PDEs in different geometries. The performance of deep learning based method depends on the configurations of the network and other hyper-parameter settings. This makes the choice of neural network configurations extremely important. The configuration of this deep collocation method is setup by comparing different schemes of smooth activation functions, sampling methods for collocation points generation, combined optimizers. Besides, a convergence proof of this deep collocation method in solving non-homogeneous potential problems is performed. Then the deep collocation method is applied to the analysis of different material variations, and it can be concluded that the deep collocation method predicts the temperature and flux accurately for different material variations, especially the exponential material variations. As a result, the deep learning based collocation method shows a great potential in approximating solutions to PDEs.

Stochastic groundwater flow analysis in heterogeneous aquifer with modified neural architecture search (NAS) based physics-informed neural networks using transfer learning

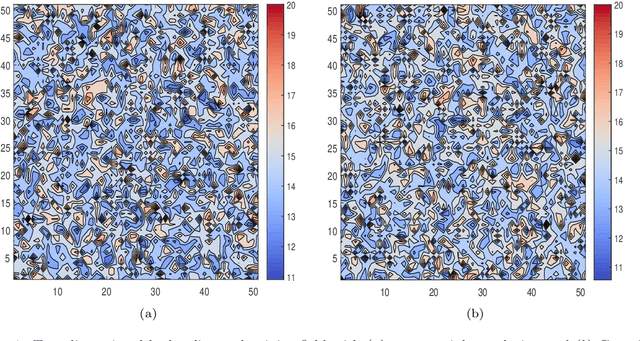
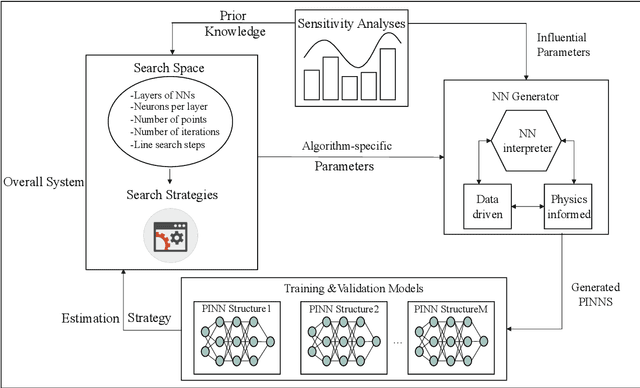
In this work, a modified neural architecture search method (NAS) based physics-informed deep learning model is presented to solve the groundwater flow problems in porous media. Monte Carlo method based on a randomized spectral representation is first employed to construct a stochastic model for simulation of flow through porous media. The desired hydraulic conductivity fields are assumed to be log-normally distributed with exponential and Gaussian correlations. To analyze the Darcy equation with the random hydraulic conductivity in this case when its intensity of fluctuations is small, the lowest-order perturbation theory is used to reduce the difficulty of calculations, by neglecting the higher-order nonlinear part. To solve the governing equations for groundwater flow problem, we build a modified NAS model based on physics-informed neural networks (PINNs) with transfer learning in this paper that will be able to fit different partial differential equations (PDEs) with less calculation. The performance estimation strategies adopted is constructed from an error estimation model using the method of manufactured solutions. Since the configuration selection of the neural network has a strong influence on the simulation results, we apply sensitivity analysis to obtain the prior knowledge of the PINNs model and narrow down the range of parameters for search space and use hyper-parameter optimization algorithms to further determine the values of the parameters. Further the NAS based PINNs model also saves the weights and biases of the most favorable architectures, which is then used in the fine-tuning process. The proposed NAS model based deep collocation method is verified to be effective and accurate through numerical examples in different dimensions using different manufactured solutions.

High correlated variables creator machine: Prediction of the compressive strength of concrete

In this paper, we introduce a novel hybrid model for predicting the compressive strength of concrete using ultrasonic pulse velocity (UPV) and rebound number (RN). First, 516 data from 8 studies of UPV and rebound hammer (RH) tests was collected. Then, high correlated variables creator machine (HVCM) is used to create the new variables that have a better correlation with the output and improve the prediction models. Three single models, including a step-by-step regression (SBSR), gene expression programming (GEP) and an adaptive neuro-fuzzy inference system (ANFIS) as well as three hybrid models, i.e. HCVCM-SBSR, HCVCM-GEP and HCVCM-ANFIS, were employed to predict the compressive strength of concrete. The statistical parameters and error terms such as coefficient of determination, root mean square error (RMSE), normalized mean square error (NMSE), fractional bias, the maximum positive and negative errors, and mean absolute percentage error (MAPE), were computed to evaluate and compare the models. The results show that HCVCM-ANFIS can predict the compressive strength of concrete better than all other models. HCVCM improves the accuracy of ANFIS by 5% in the coefficient of determination, 10% in RMSE, 3% in NMSE, 20% in MAPE, and 7% in the maximum negative error.