Generalization capabilities of MeshGraphNets to unseen geometries for fluid dynamics

This works investigates the generalization capabilities of MeshGraphNets (MGN) [Pfaff et al. Learning Mesh-Based Simulation with Graph Networks. ICML 2021] to unseen geometries for fluid dynamics, e.g. predicting the flow around a new obstacle that was not part of the training data. For this purpose, we create a new benchmark dataset for data-driven computational fluid dynamics (CFD) which extends DeepMind's flow around a cylinder dataset by including different shapes and multiple objects. We then use this new dataset to extend the generalization experiments conducted by DeepMind on MGNs by testing how well an MGN can generalize to different shapes. In our numerical tests, we show that MGNs can sometimes generalize well to various shapes by training on a dataset of one obstacle shape and testing on a dataset of another obstacle shape.

Multigoal-oriented dual-weighted-residual error estimation using deep neural networks

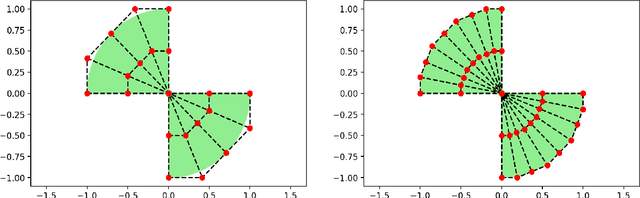
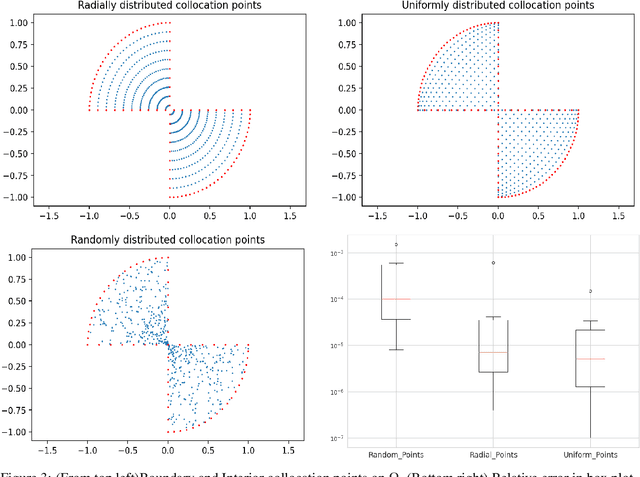
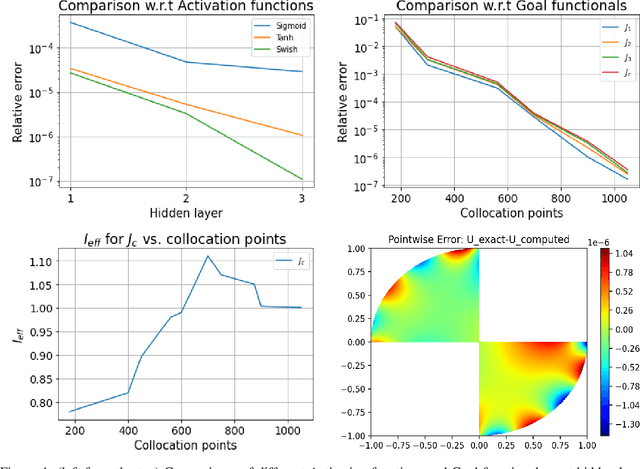
Deep learning has shown successful application in visual recognition and certain artificial intelligence tasks. Deep learning is also considered as a powerful tool with high flexibility to approximate functions. In the present work, functions with desired properties are devised to approximate the solutions of PDEs. Our approach is based on a posteriori error estimation in which the adjoint problem is solved for the error localization to formulate an error estimator within the framework of neural network. An efficient and easy to implement algorithm is developed to obtain a posteriori error estimate for multiple goal functionals by employing the dual-weighted residual approach, which is followed by the computation of both primal and adjoint solutions using the neural network. The present study shows that such a data-driven model based learning has superior approximation of quantities of interest even with relatively less training data. The novel algorithmic developments are substantiated with numerical test examples. The advantages of using deep neural network over the shallow neural network are demonstrated and the convergence enhancing techniques are also presented