Generalization capabilities of MeshGraphNets to unseen geometries for fluid dynamics

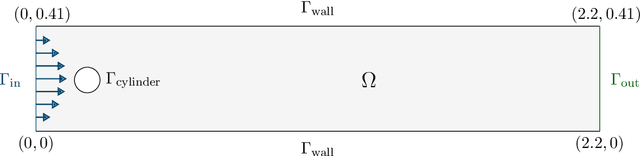
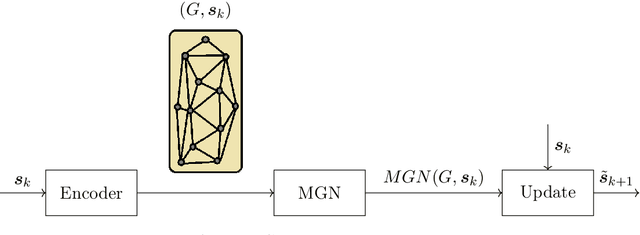
This works investigates the generalization capabilities of MeshGraphNets (MGN) [Pfaff et al. Learning Mesh-Based Simulation with Graph Networks. ICML 2021] to unseen geometries for fluid dynamics, e.g. predicting the flow around a new obstacle that was not part of the training data. For this purpose, we create a new benchmark dataset for data-driven computational fluid dynamics (CFD) which extends DeepMind's flow around a cylinder dataset by including different shapes and multiple objects. We then use this new dataset to extend the generalization experiments conducted by DeepMind on MGNs by testing how well an MGN can generalize to different shapes. In our numerical tests, we show that MGNs can sometimes generalize well to various shapes by training on a dataset of one obstacle shape and testing on a dataset of another obstacle shape.

Deterministic and statistical calibration of constitutive models from full-field data with parametric physics-informed neural networks

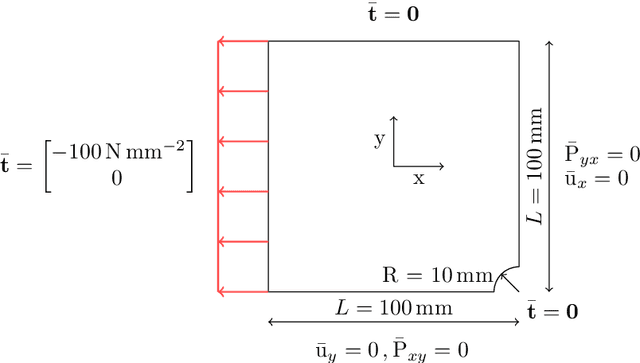
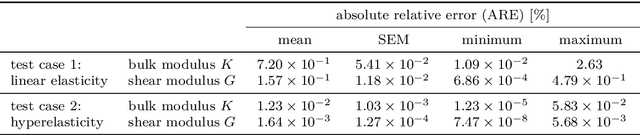
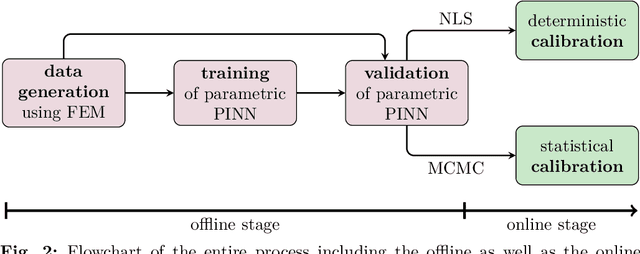
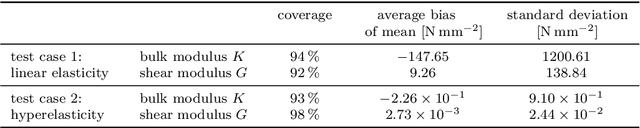
The calibration of constitutive models from full-field data has recently gained increasing interest due to improvements in full-field measurement capabilities. In addition to the experimental characterization of novel materials, continuous structural health monitoring is another application that is of great interest. However, monitoring is usually associated with severe time constraints, difficult to meet with standard numerical approaches. Therefore, parametric physics-informed neural networks (PINNs) for constitutive model calibration from full-field displacement data are investigated. In an offline stage, a parametric PINN can be trained to learn a parameterized solution of the underlying partial differential equation. In the subsequent online stage, the parametric PINN then acts as a surrogate for the parameters-to-state map in calibration. We test the proposed approach for the deterministic least-squares calibration of a linear elastic as well as a hyperelastic constitutive model from noisy synthetic displacement data. We further carry out Markov chain Monte Carlo-based Bayesian inference to quantify the uncertainty. A proper statistical evaluation of the results underlines the high accuracy of the deterministic calibration and that the estimated uncertainty is valid. Finally, we consider experimental data and show that the results are in good agreement with a Finite Element Method-based calibration. Due to the fast evaluation of PINNs, calibration can be performed in near real-time. This advantage is particularly evident in many-query applications such as Markov chain Monte Carlo-based Bayesian inference.

Spiking neural network for nonlinear regression

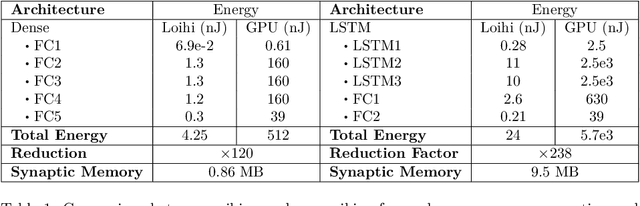
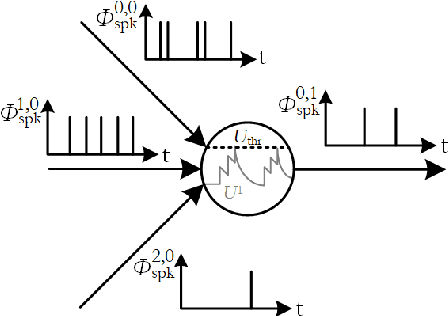
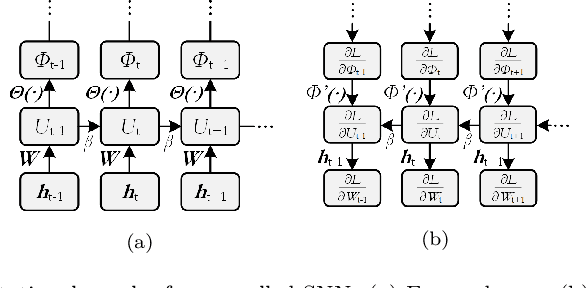
Spiking neural networks, also often referred to as the third generation of neural networks, carry the potential for a massive reduction in memory and energy consumption over traditional, second-generation neural networks. Inspired by the undisputed efficiency of the human brain, they introduce temporal and neuronal sparsity, which can be exploited by next-generation neuromorphic hardware. To open the pathway toward engineering applications, we introduce this exciting technology in the context of continuum mechanics. However, the nature of spiking neural networks poses a challenge for regression problems, which frequently arise in the modeling of engineering sciences. To overcome this problem, a framework for regression using spiking neural networks is proposed. In particular, a network topology for decoding binary spike trains to real numbers is introduced, utilizing the membrane potential of spiking neurons. As the aim of this contribution is a concise introduction to this new methodology, several different spiking neural architectures, ranging from simple spiking feed-forward to complex spiking long short-term memory neural networks, are derived. Several numerical experiments directed towards regression of linear and nonlinear, history-dependent material models are carried out. A direct comparison with counterparts of traditional neural networks shows that the proposed framework is much more efficient while retaining precision and generalizability. All code has been made publicly available in the interest of reproducibility and to promote continued enhancement in this new domain.

Three-dimensional microstructure generation using generative adversarial neural networks in the context of continuum micromechanics

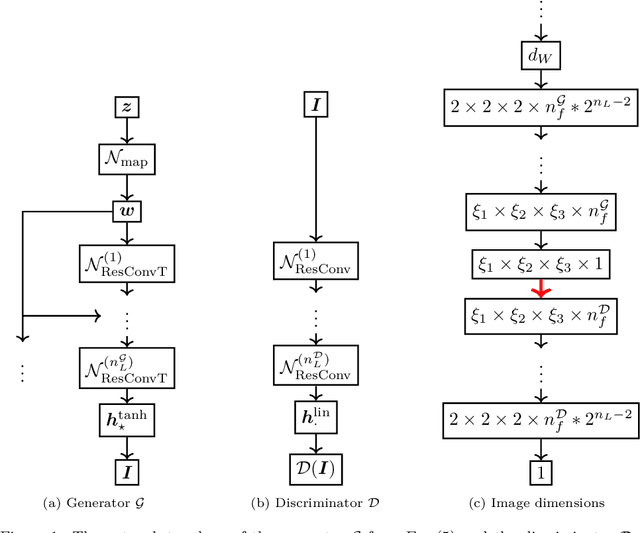
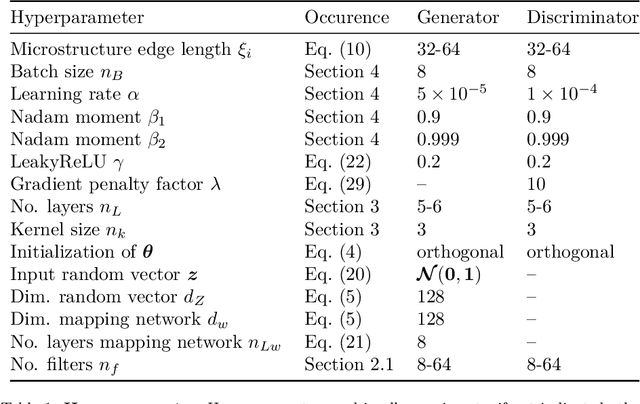
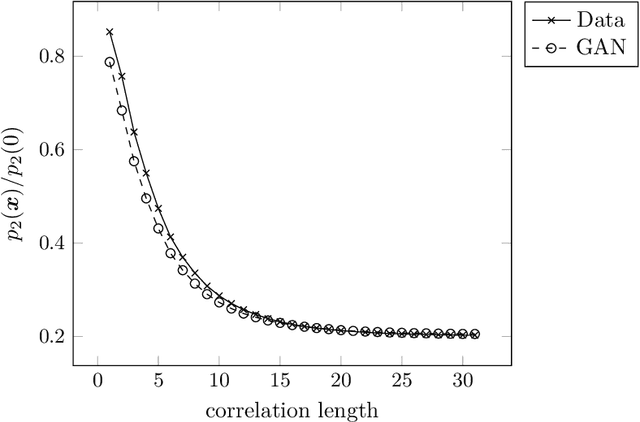
Multiscale simulations are demanding in terms of computational resources. In the context of continuum micromechanics, the multiscale problem arises from the need of inferring macroscopic material parameters from the microscale. If the underlying microstructure is explicitly given by means of microCT-scans, convolutional neural networks can be used to learn the microstructure-property mapping, which is usually obtained from computational homogenization. The CNN approach provides a significant speedup, especially in the context of heterogeneous or functionally graded materials. Another application is uncertainty quantification, where many expansive evaluations are required. However, one bottleneck of this approach is the large number of training microstructures needed. This work closes this gap by proposing a generative adversarial network tailored towards three-dimensional microstructure generation. The lightweight algorithm is able to learn the underlying properties of the material from a single microCT-scan without the need of explicit descriptors. During prediction time, the network can produce unique three-dimensional microstructures with the same properties of the original data in a fraction of seconds and at consistently high quality.

A deep learning driven pseudospectral PCE based FFT homogenization algorithm for complex microstructures

This work is directed to uncertainty quantification of homogenized effective properties for composite materials with complex, three dimensional microstructure. The uncertainties arise in the material parameters of the single constituents as well as in the fiber volume fraction. They are taken into account by multivariate random variables. Uncertainty quantification is achieved by an efficient surrogate model based on pseudospectral polynomial chaos expansion and artificial neural networks. An artificial neural network is trained on synthetic binary voxelized unit cells of composite materials with uncertain three dimensional microstructures, uncertain linear elastic material parameters and different loading directions. The prediction goals of the artificial neural network are the corresponding effective components of the elasticity tensor, where the labels for training are generated via a fast Fourier transform based numerical homogenization method. The trained artificial neural network is then used as a deterministic solver for a pseudospectral polynomial chaos expansion based surrogate model to achieve the corresponding statistics of the effective properties. Three numerical examples deal with the comparison of the presented method to the literature as well as the application to different microstructures. It is shown, that the proposed method is able to predict central moments of interest while being magnitudes faster to evaluate than traditional approaches.

Physics informed neural networks for continuum micromechanics

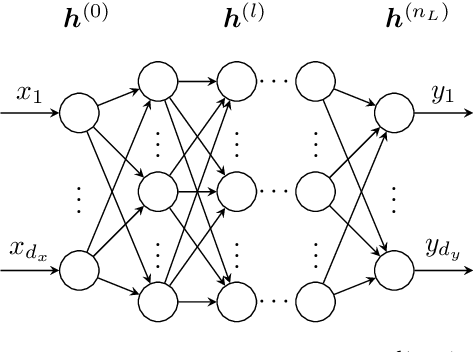
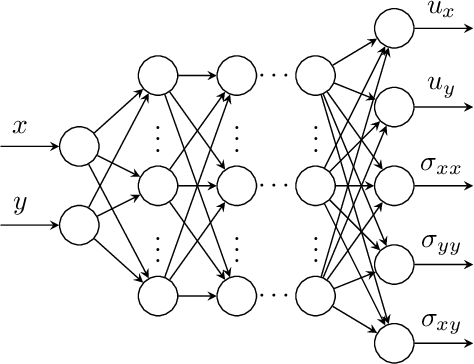
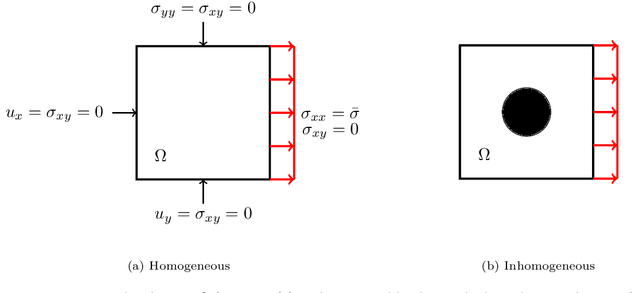
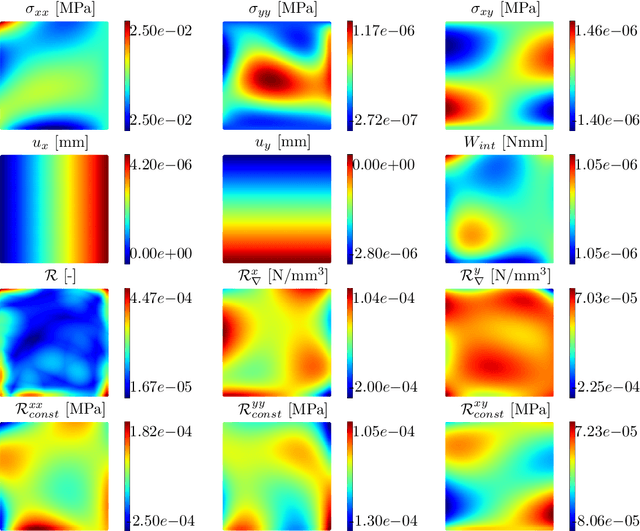
Recently, physics informed neural networks have successfully been applied to a broad variety of problems in applied mathematics and engineering. The principle idea is to use a neural network as a global ansatz function to partial differential equations. Due to the global approximation, physics informed neural networks have difficulties in displaying localized effects and strong non-linear solutions by optimization. In this work we consider material non-linearities invoked by material inhomogeneities with sharp phase interfaces. This constitutes a challenging problem for a method relying on a global ansatz. To overcome convergence issues, adaptive training strategies and domain decomposition are studied. It is shown, that the domain decomposition approach is able to accurately resolve nonlinear stress, displacement and energy fields in heterogeneous microstructures obtained from real-world $\mu$CT-scans.