Automated Constitutive Model Discovery by Pairing Sparse Regression Algorithms with Model Selection Criteria

The automated discovery of constitutive models from data has recently emerged as a promising alternative to the traditional model calibration paradigm. In this work, we present a fully automated framework for constitutive model discovery that systematically pairs three sparse regression algorithms (Least Absolute Shrinkage and Selection Operator (LASSO), Least Angle Regression (LARS), and Orthogonal Matching Pursuit (OMP)) with three model selection criteria: $K$-fold cross-validation (CV), Akaike Information Criterion (AIC), and Bayesian Information Criterion (BIC). This pairing yields nine distinct algorithms for model discovery and enables a systematic exploration of the trade-off between sparsity, predictive performance, and computational cost. While LARS serves as an efficient path-based solver for the $\ell_1$-constrained problem, OMP is introduced as a tractable heuristic for $\ell_0$-regularized selection. The framework is applied to both isotropic and anisotropic hyperelasticity, utilizing both synthetic and experimental datasets. Results reveal that all nine algorithm-criterion combinations perform consistently well for the discovery of isotropic and anisotropic materials, yielding highly accurate constitutive models. These findings broaden the range of viable discovery algorithms beyond $\ell_1$-based approaches such as LASSO.

Drivetrain simulation using variational autoencoders

This work proposes variational autoencoders (VAEs) to predict a vehicle's jerk from a given torque demand, addressing the limitations of sparse real-world datasets. Specifically, we implement unconditional and conditional VAEs to generate jerk signals that integrate features from different drivetrain scenarios. The VAEs are trained on experimental data collected from two variants of a fully electric SUV, which differ in maximum torque delivery and drivetrain configuration. New meaningful jerk signals are generated within an engineering context through the interpretation of the VAE's latent space. A performance comparison with baseline physics-based and hybrid models confirms the effectiveness of the VAEs. We show that VAEs bypass the need for exhaustive manual system parametrization while maintaining physical plausibility by conditioning data generation on specific inputs.

Deterministic and statistical calibration of constitutive models from full-field data with parametric physics-informed neural networks

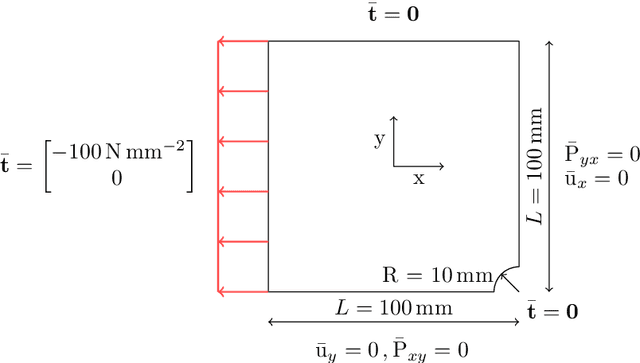
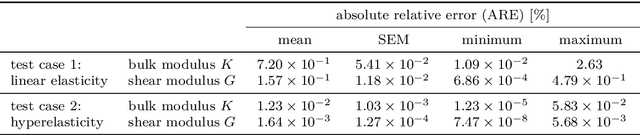
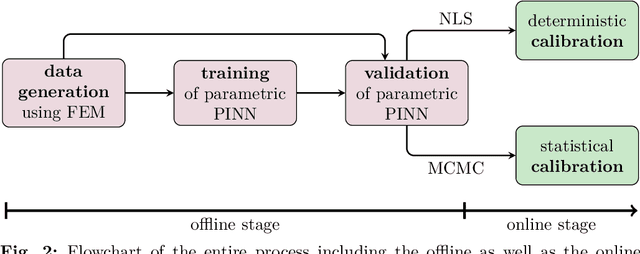
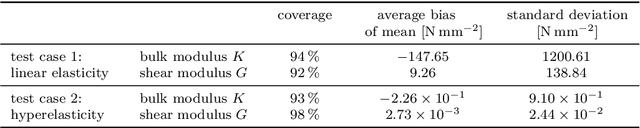
The calibration of constitutive models from full-field data has recently gained increasing interest due to improvements in full-field measurement capabilities. In addition to the experimental characterization of novel materials, continuous structural health monitoring is another application that is of great interest. However, monitoring is usually associated with severe time constraints, difficult to meet with standard numerical approaches. Therefore, parametric physics-informed neural networks (PINNs) for constitutive model calibration from full-field displacement data are investigated. In an offline stage, a parametric PINN can be trained to learn a parameterized solution of the underlying partial differential equation. In the subsequent online stage, the parametric PINN then acts as a surrogate for the parameters-to-state map in calibration. We test the proposed approach for the deterministic least-squares calibration of a linear elastic as well as a hyperelastic constitutive model from noisy synthetic displacement data. We further carry out Markov chain Monte Carlo-based Bayesian inference to quantify the uncertainty. A proper statistical evaluation of the results underlines the high accuracy of the deterministic calibration and that the estimated uncertainty is valid. Finally, we consider experimental data and show that the results are in good agreement with a Finite Element Method-based calibration. Due to the fast evaluation of PINNs, calibration can be performed in near real-time. This advantage is particularly evident in many-query applications such as Markov chain Monte Carlo-based Bayesian inference.

Physics-Informed Neural Networks for Material Model Calibration from Full-Field Displacement Data

The identification of material parameters occurring in constitutive models has a wide range of applications in practice. One of these applications is the monitoring and assessment of the actual condition of infrastructure buildings, as the material parameters directly reflect the resistance of the structures to external impacts. Physics-informed neural networks (PINNs) have recently emerged as a suitable method for solving inverse problems. The advantages of this method are a straightforward inclusion of observation data. Unlike grid-based methods, such as the finite element method updating (FEMU) approach, no computational grid and no interpolation of the data is required. In the current work, we aim to further develop PINNs towards the calibration of the linear-elastic constitutive model from full-field displacement and global force data in a realistic regime. We show that normalization and conditioning of the optimization problem play a crucial role in this process. Therefore, among others, we identify the material parameters for initial estimates and balance the individual terms in the loss function. In order to reduce the dependence of the identified material parameters on local errors in the displacement approximation, we base the identification not on the stress boundary conditions but instead on the global balance of internal and external work. In addition, we found that we get a better posed inverse problem if we reformulate it in terms of bulk and shear modulus instead of Young's modulus and Poisson's ratio. We demonstrate that the enhanced PINNs are capable of identifying material parameters from both experimental one-dimensional data and synthetic full-field displacement data in a realistic regime. Since displacement data measured by, e.g., a digital image correlation (DIC) system is noisy, we additionally investigate the robustness of the method to different levels of noise.

Spiking neural network for nonlinear regression

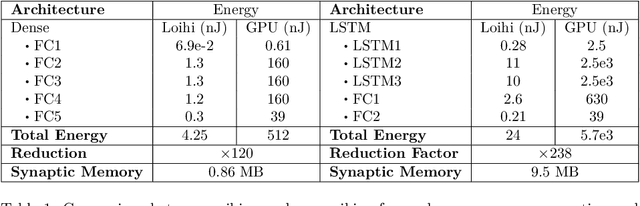
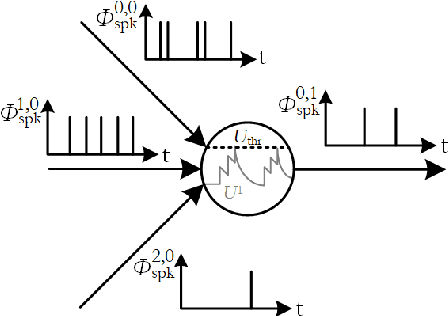
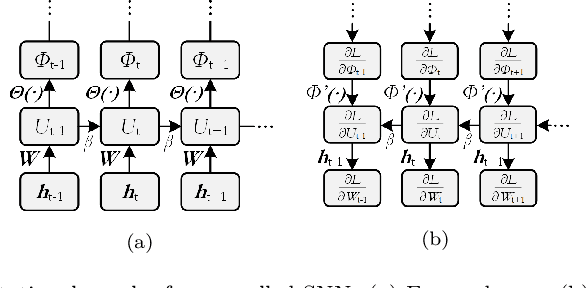
Spiking neural networks, also often referred to as the third generation of neural networks, carry the potential for a massive reduction in memory and energy consumption over traditional, second-generation neural networks. Inspired by the undisputed efficiency of the human brain, they introduce temporal and neuronal sparsity, which can be exploited by next-generation neuromorphic hardware. To open the pathway toward engineering applications, we introduce this exciting technology in the context of continuum mechanics. However, the nature of spiking neural networks poses a challenge for regression problems, which frequently arise in the modeling of engineering sciences. To overcome this problem, a framework for regression using spiking neural networks is proposed. In particular, a network topology for decoding binary spike trains to real numbers is introduced, utilizing the membrane potential of spiking neurons. As the aim of this contribution is a concise introduction to this new methodology, several different spiking neural architectures, ranging from simple spiking feed-forward to complex spiking long short-term memory neural networks, are derived. Several numerical experiments directed towards regression of linear and nonlinear, history-dependent material models are carried out. A direct comparison with counterparts of traditional neural networks shows that the proposed framework is much more efficient while retaining precision and generalizability. All code has been made publicly available in the interest of reproducibility and to promote continued enhancement in this new domain.

Three-dimensional microstructure generation using generative adversarial neural networks in the context of continuum micromechanics

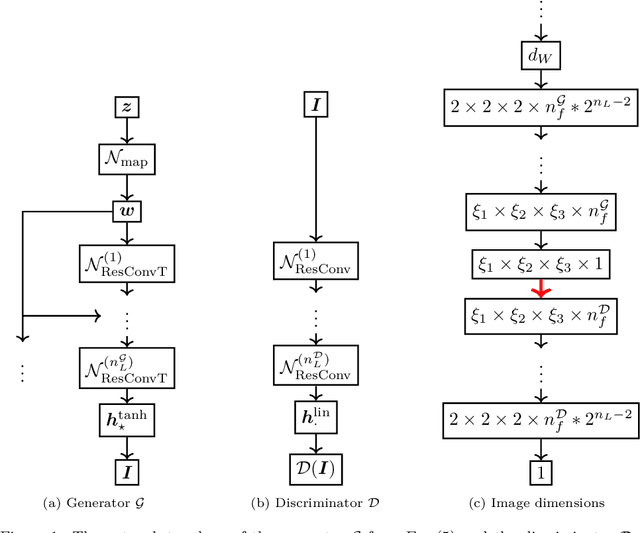
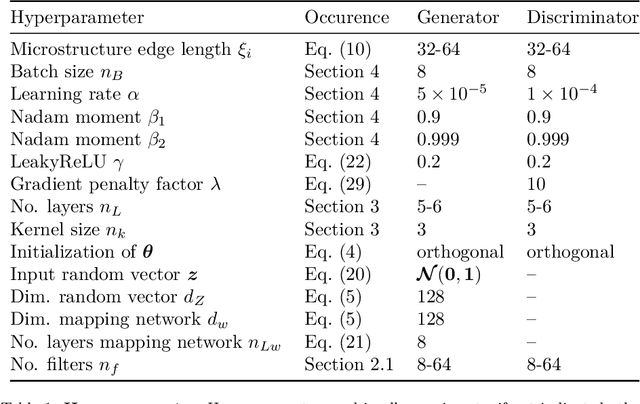
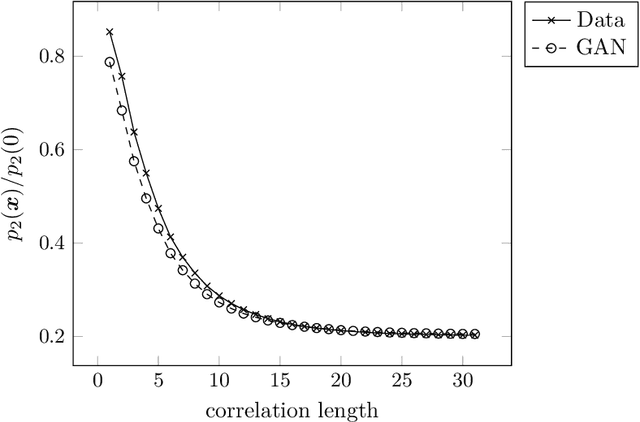
Multiscale simulations are demanding in terms of computational resources. In the context of continuum micromechanics, the multiscale problem arises from the need of inferring macroscopic material parameters from the microscale. If the underlying microstructure is explicitly given by means of microCT-scans, convolutional neural networks can be used to learn the microstructure-property mapping, which is usually obtained from computational homogenization. The CNN approach provides a significant speedup, especially in the context of heterogeneous or functionally graded materials. Another application is uncertainty quantification, where many expansive evaluations are required. However, one bottleneck of this approach is the large number of training microstructures needed. This work closes this gap by proposing a generative adversarial network tailored towards three-dimensional microstructure generation. The lightweight algorithm is able to learn the underlying properties of the material from a single microCT-scan without the need of explicit descriptors. During prediction time, the network can produce unique three-dimensional microstructures with the same properties of the original data in a fraction of seconds and at consistently high quality.

Physics informed neural networks for continuum micromechanics

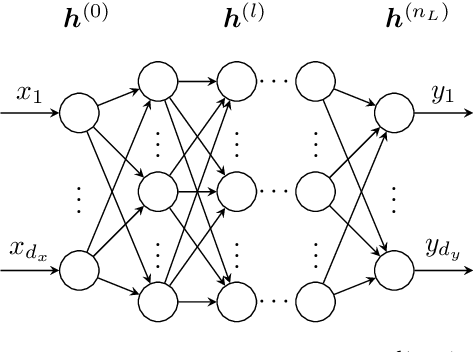
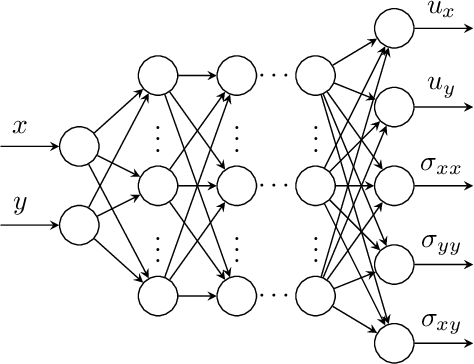
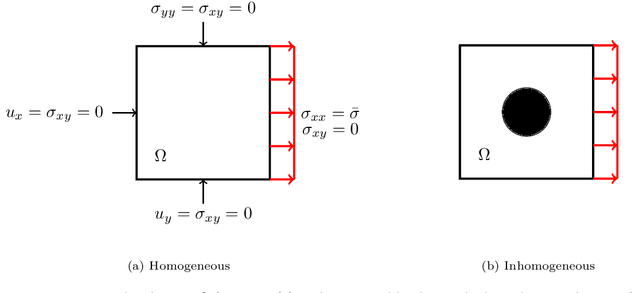
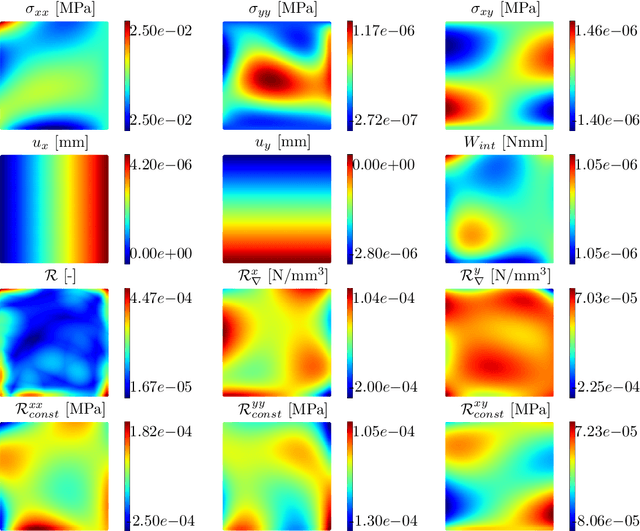
Recently, physics informed neural networks have successfully been applied to a broad variety of problems in applied mathematics and engineering. The principle idea is to use a neural network as a global ansatz function to partial differential equations. Due to the global approximation, physics informed neural networks have difficulties in displaying localized effects and strong non-linear solutions by optimization. In this work we consider material non-linearities invoked by material inhomogeneities with sharp phase interfaces. This constitutes a challenging problem for a method relying on a global ansatz. To overcome convergence issues, adaptive training strategies and domain decomposition are studied. It is shown, that the domain decomposition approach is able to accurately resolve nonlinear stress, displacement and energy fields in heterogeneous microstructures obtained from real-world $\mu$CT-scans.