A deep learning driven pseudospectral PCE based FFT homogenization algorithm for complex microstructures

This work is directed to uncertainty quantification of homogenized effective properties for composite materials with complex, three dimensional microstructure. The uncertainties arise in the material parameters of the single constituents as well as in the fiber volume fraction. They are taken into account by multivariate random variables. Uncertainty quantification is achieved by an efficient surrogate model based on pseudospectral polynomial chaos expansion and artificial neural networks. An artificial neural network is trained on synthetic binary voxelized unit cells of composite materials with uncertain three dimensional microstructures, uncertain linear elastic material parameters and different loading directions. The prediction goals of the artificial neural network are the corresponding effective components of the elasticity tensor, where the labels for training are generated via a fast Fourier transform based numerical homogenization method. The trained artificial neural network is then used as a deterministic solver for a pseudospectral polynomial chaos expansion based surrogate model to achieve the corresponding statistics of the effective properties. Three numerical examples deal with the comparison of the presented method to the literature as well as the application to different microstructures. It is shown, that the proposed method is able to predict central moments of interest while being magnitudes faster to evaluate than traditional approaches.

Physics informed neural networks for continuum micromechanics

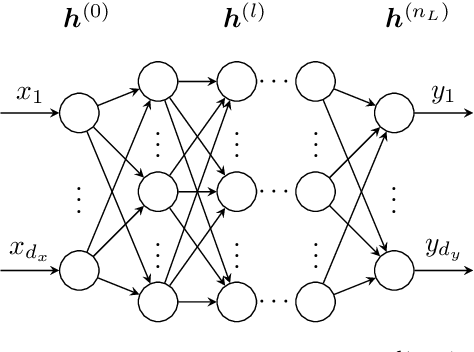
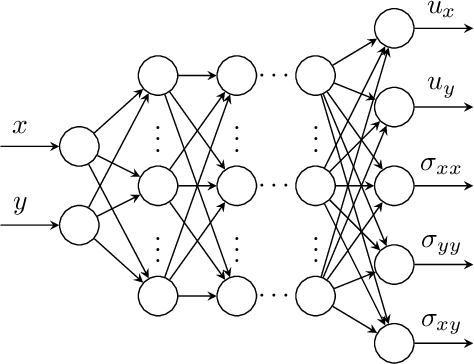
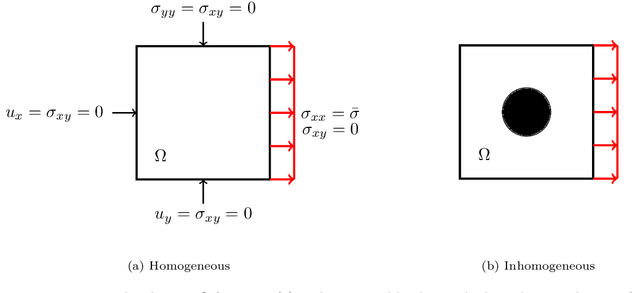
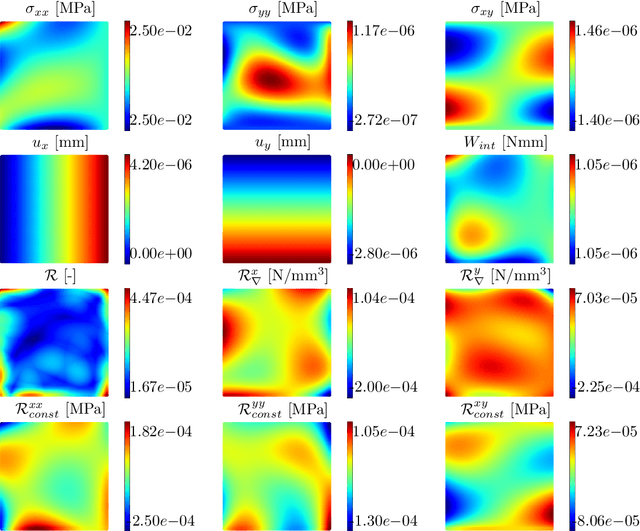
Recently, physics informed neural networks have successfully been applied to a broad variety of problems in applied mathematics and engineering. The principle idea is to use a neural network as a global ansatz function to partial differential equations. Due to the global approximation, physics informed neural networks have difficulties in displaying localized effects and strong non-linear solutions by optimization. In this work we consider material non-linearities invoked by material inhomogeneities with sharp phase interfaces. This constitutes a challenging problem for a method relying on a global ansatz. To overcome convergence issues, adaptive training strategies and domain decomposition are studied. It is shown, that the domain decomposition approach is able to accurately resolve nonlinear stress, displacement and energy fields in heterogeneous microstructures obtained from real-world $\mu$CT-scans.