Deterministic and statistical calibration of constitutive models from full-field data with parametric physics-informed neural networks

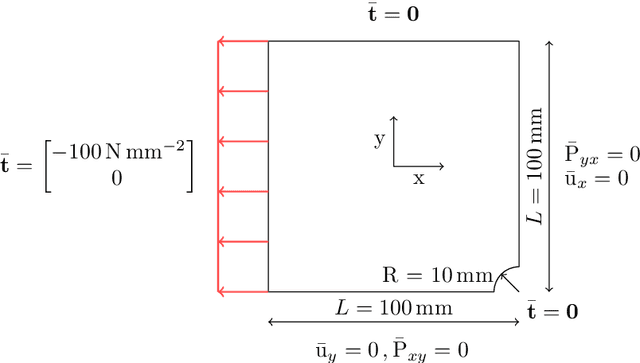
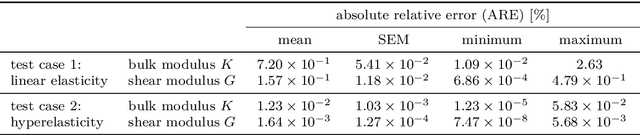
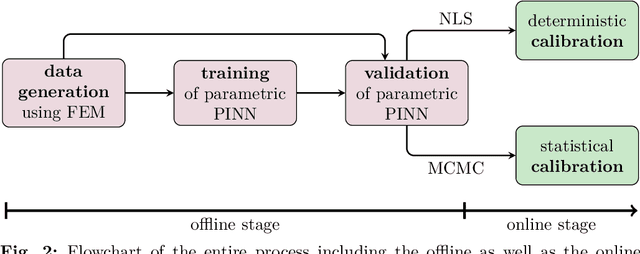
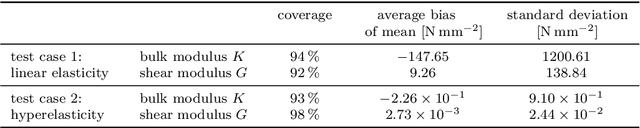
The calibration of constitutive models from full-field data has recently gained increasing interest due to improvements in full-field measurement capabilities. In addition to the experimental characterization of novel materials, continuous structural health monitoring is another application that is of great interest. However, monitoring is usually associated with severe time constraints, difficult to meet with standard numerical approaches. Therefore, parametric physics-informed neural networks (PINNs) for constitutive model calibration from full-field displacement data are investigated. In an offline stage, a parametric PINN can be trained to learn a parameterized solution of the underlying partial differential equation. In the subsequent online stage, the parametric PINN then acts as a surrogate for the parameters-to-state map in calibration. We test the proposed approach for the deterministic least-squares calibration of a linear elastic as well as a hyperelastic constitutive model from noisy synthetic displacement data. We further carry out Markov chain Monte Carlo-based Bayesian inference to quantify the uncertainty. A proper statistical evaluation of the results underlines the high accuracy of the deterministic calibration and that the estimated uncertainty is valid. Finally, we consider experimental data and show that the results are in good agreement with a Finite Element Method-based calibration. Due to the fast evaluation of PINNs, calibration can be performed in near real-time. This advantage is particularly evident in many-query applications such as Markov chain Monte Carlo-based Bayesian inference.

Enhancing Multiscale Simulations with Constitutive Relations-Aware Deep Operator Networks

Multiscale problems are widely observed across diverse domains in physics and engineering. Translating these problems into numerical simulations and solving them using numerical schemes, e.g. the finite element method, is costly due to the demand of solving initial boundary-value problems at multiple scales. On the other hand, multiscale finite element computations are commended for their ability to integrate micro-structural properties into macroscopic computational analyses using homogenization techniques. Recently, neural operator-based surrogate models have shown trustworthy performance for solving a wide range of partial differential equations. In this work, we propose a hybrid method in which we utilize deep operator networks for surrogate modeling of the microscale physics. This allows us to embed the constitutive relations of the microscale into the model architecture and to predict microscale strains and stresses based on the prescribed macroscale strain inputs. Furthermore, numerical homogenization is carried out to obtain the macroscale quantities of interest. We apply the proposed approach to quasi-static problems of solid mechanics. The results demonstrate that our constitutive relations-aware DeepONet can yield accurate solutions even when being confronted with a restricted dataset during model development.