DiffBatt: A Diffusion Model for Battery Degradation Prediction and Synthesis

Battery degradation remains a critical challenge in the pursuit of green technologies and sustainable energy solutions. Despite significant research efforts, predicting battery capacity loss accurately remains a formidable task due to its complex nature, influenced by both aging and cycling behaviors. To address this challenge, we introduce a novel general-purpose model for battery degradation prediction and synthesis, DiffBatt. Leveraging an innovative combination of conditional and unconditional diffusion models with classifier-free guidance and transformer architecture, DiffBatt achieves high expressivity and scalability. DiffBatt operates as a probabilistic model to capture uncertainty in aging behaviors and a generative model to simulate battery degradation. The performance of the model excels in prediction tasks while also enabling the generation of synthetic degradation curves, facilitating enhanced model training by data augmentation. In the remaining useful life prediction task, DiffBatt provides accurate results with a mean RMSE of 196 cycles across all datasets, outperforming all other models and demonstrating superior generalizability. This work represents an important step towards developing foundational models for battery degradation.

Enhancing Multiscale Simulations with Constitutive Relations-Aware Deep Operator Networks

Multiscale problems are widely observed across diverse domains in physics and engineering. Translating these problems into numerical simulations and solving them using numerical schemes, e.g. the finite element method, is costly due to the demand of solving initial boundary-value problems at multiple scales. On the other hand, multiscale finite element computations are commended for their ability to integrate micro-structural properties into macroscopic computational analyses using homogenization techniques. Recently, neural operator-based surrogate models have shown trustworthy performance for solving a wide range of partial differential equations. In this work, we propose a hybrid method in which we utilize deep operator networks for surrogate modeling of the microscale physics. This allows us to embed the constitutive relations of the microscale into the model architecture and to predict microscale strains and stresses based on the prescribed macroscale strain inputs. Furthermore, numerical homogenization is carried out to obtain the macroscale quantities of interest. We apply the proposed approach to quasi-static problems of solid mechanics. The results demonstrate that our constitutive relations-aware DeepONet can yield accurate solutions even when being confronted with a restricted dataset during model development.

Nonlinear model reduction for operator learning

Operator learning provides methods to approximate mappings between infinite-dimensional function spaces. Deep operator networks (DeepONets) are a notable architecture in this field. Recently, an extension of DeepONet based on model reduction and neural networks, proper orthogonal decomposition (POD)-DeepONet, has been able to outperform other architectures in terms of accuracy for several benchmark tests. We extend this idea towards nonlinear model order reduction by proposing an efficient framework that combines neural networks with kernel principal component analysis (KPCA) for operator learning. Our results demonstrate the superior performance of KPCA-DeepONet over POD-DeepONet.

Physics-Informed Transfer Learning Strategy to Accelerate Unsteady Fluid Flow Simulations

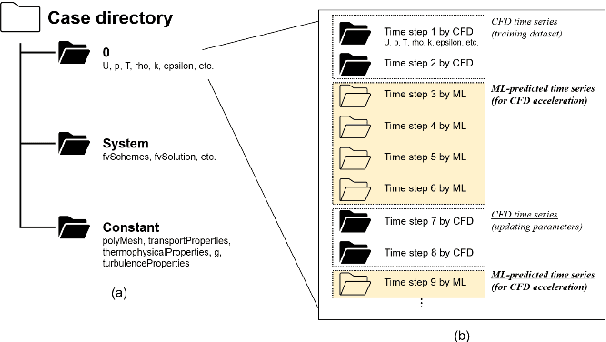
Since the derivation of the Navier Stokes equations, it has become possible to numerically solve real world viscous flow problems (computational fluid dynamics (CFD)). However, despite the rapid advancements in the performance of central processing units (CPUs), the computational cost of simulating transient flows with extremely small time/grid scale physics is still unrealistic. In recent years, machine learning (ML) technology has received significant attention across industries, and this big wave has propagated various interests in the fluid dynamics community. Recent ML CFD studies have revealed that completely suppressing the increase in error with the increase in interval between the training and prediction times in data driven methods is unrealistic. The development of a practical CFD acceleration methodology that applies ML is a remaining issue. Therefore, the objectives of this study were developing a realistic ML strategy based on a physics-informed transfer learning and validating the accuracy and acceleration performance of this strategy using an unsteady CFD dataset. This strategy can determine the timing of transfer learning while monitoring the residuals of the governing equations in a cross coupling computation framework. Consequently, our hypothesis that continuous fluid flow time series prediction is feasible was validated, as the intermediate CFD simulations periodically not only reduce the increased residuals but also update the network parameters. Notably, the cross coupling strategy with a grid based network model does not compromise the simulation accuracy for computational acceleration. The simulation was accelerated by 1.8 times in the laminar counterflow CFD dataset condition including the parameter updating time. Open source CFD software OpenFOAM and open-source ML software TensorFlow were used in this feasibility study.

Physics-informed deep-learning applications to experimental fluid mechanics

High-resolution reconstruction of flow-field data from low-resolution and noisy measurements is of interest due to the prevalence of such problems in experimental fluid mechanics, where the measurement data are in general sparse, incomplete and noisy. Deep-learning approaches have been shown suitable for such super-resolution tasks. However, a high number of high-resolution examples is needed, which may not be available for many cases. Moreover, the obtained predictions may lack in complying with the physical principles, e.g. mass and momentum conservation. Physics-informed deep learning provides frameworks for integrating data and physical laws for learning. In this study, we apply physics-informed neural networks (PINNs) for super-resolution of flow-field data both in time and space from a limited set of noisy measurements without having any high-resolution reference data. Our objective is to obtain a continuous solution of the problem, providing a physically-consistent prediction at any point in the solution domain. We demonstrate the applicability of PINNs for the super-resolution of flow-field data in time and space through three canonical cases: Burgers' equation, two-dimensional vortex shedding behind a circular cylinder and the minimal turbulent channel flow. The robustness of the models is also investigated by adding synthetic Gaussian noise. Our results show excellent capabilities of PINNs in the context of data augmentation for experiments in fluid mechanics.

Predicting the temporal dynamics of turbulent channels through deep learning

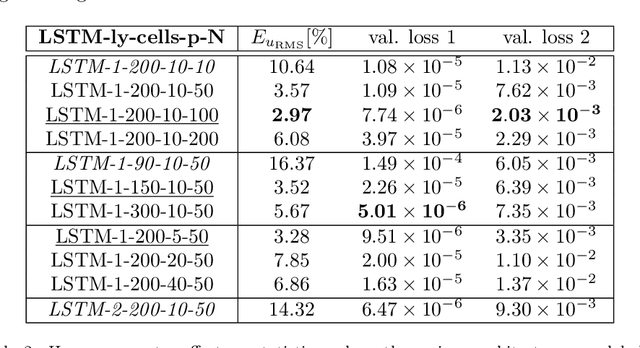
The success of recurrent neural networks (RNNs) has been demonstrated in many applications related to turbulence, including flow control, optimization, turbulent features reproduction as well as turbulence prediction and modeling. With this study we aim to assess the capability of these networks to reproduce the temporal evolution of a minimal turbulent channel flow. We first obtain a data-driven model based on a modal decomposition in the Fourier domain (which we denote as FFT-POD) of the time series sampled from the flow. This particular case of turbulent flow allows us to accurately simulate the most relevant coherent structures close to the wall. Long-short-term-memory (LSTM) networks and a Koopman-based framework (KNF) are trained to predict the temporal dynamics of the minimal-channel-flow modes. Tests with different configurations highlight the limits of the KNF method compared to the LSTM, given the complexity of the flow under study. Long-term prediction for LSTM show excellent agreement from the statistical point of view, with errors below 2% for the best models with respect to the reference. Furthermore, the analysis of the chaotic behaviour through the use of the Lyapunov exponents and of the dynamic behaviour through Poincar\'e maps emphasizes the ability of the LSTM to reproduce the temporal dynamics of turbulence. Alternative reduced-order models (ROMs), based on the identification of different turbulent structures, are explored and they continue to show a good potential in predicting the temporal dynamics of the minimal channel.

Towards extraction of orthogonal and parsimonious non-linear modes from turbulent flows

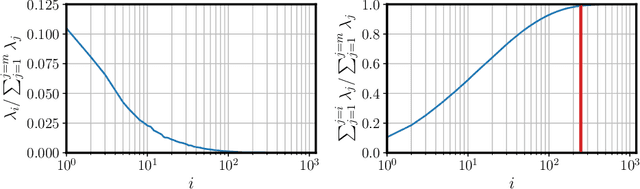
We propose a deep probabilistic-neural-network architecture for learning a minimal and near-orthogonal set of non-linear modes from high-fidelity turbulent-flow-field data useful for flow analysis, reduced-order modeling, and flow control. Our approach is based on $\beta$-variational autoencoders ($\beta$-VAEs) and convolutional neural networks (CNNs), which allow us to extract non-linear modes from multi-scale turbulent flows while encouraging the learning of independent latent variables and penalizing the size of the latent vector. Moreover, we introduce an algorithm for ordering VAE-based modes with respect to their contribution to the reconstruction. We apply this method for non-linear mode decomposition of the turbulent flow through a simplified urban environment, where the flow-field data is obtained based on well-resolved large-eddy simulations (LESs). We demonstrate that by constraining the shape of the latent space, it is possible to motivate the orthogonality and extract a set of parsimonious modes sufficient for high-quality reconstruction. Our results show the excellent performance of the method in the reconstruction against linear-theory-based decompositions. Moreover, we compare our method with available AE-based models. We show the ability of our approach in the extraction of near-orthogonal modes that may lead to interpretability.

Physics-informed neural networks for solving Reynolds-averaged Navier$\unicode{x2013}$Stokes equations

Physics-informed neural networks (PINNs) are successful machine-learning methods for the solution and identification of partial differential equations (PDEs). We employ PINNs for solving the Reynolds-averaged Navier$\unicode{x2013}$Stokes (RANS) equations for incompressible turbulent flows without any specific model or assumption for turbulence, and by taking only the data on the domain boundaries. We first show the applicability of PINNs for solving the Navier$\unicode{x2013}$Stokes equations for laminar flows by solving the Falkner$\unicode{x2013}$Skan boundary layer. We then apply PINNs for the simulation of four turbulent-flow cases, i.e., zero-pressure-gradient boundary layer, adverse-pressure-gradient boundary layer, and turbulent flows over a NACA4412 airfoil and the periodic hill. Our results show the excellent applicability of PINNs for laminar flows with strong pressure gradients, where predictions with less than 1% error can be obtained. For turbulent flows, we also obtain very good accuracy on simulation results even for the Reynolds-stress components.

Deep Neural Networks for Nonlinear Model Order Reduction of Unsteady Flows

Unsteady fluid systems are nonlinear high-dimensional dynamical systems that may exhibit multiple complex phenomena both in time and space. Reduced order modeling (ROM) of fluid flows has been an active research topic in the recent decade with the primary goal to decompose complex flows to a set of features most important for future state prediction and control, typically using a dimensionality reduction technique. In this work, a novel data-driven technique based on the power of deep neural networks for reduced order modeling of the unsteady fluid flows is introduced. An autoencoder network is used for nonlinear dimension reduction and feature extraction as an alternative for singular value decomposition (SVD). Then, the extracted features are used as an input for long short-term memory network (LSTM) to predict the velocity field at future time instances. The proposed autoencoder-LSTM method is compared with dynamic mode decomposition (DMD) as the data-driven base method. Moreover, an autoencoder-DMD algorithm is introduced for reduced order modeling, which uses the autoencoder network for dimensionality reduction rather than SVD rank truncation. Results show that the autoencoder-LSTM method is considerably capable of predicting the fluid flow evolution, where higher values for coefficient of determination $R^{2}$ are obtained using autoencoder-LSTM comparing to DMD.

Recurrent neural networks and Koopman-based frameworks for temporal predictions in turbulence

The prediction capabilities of recurrent neural networks and Koopman-based frameworks are assessed in the low-order model of near-wall turbulence by Moehlis et al. (New J. Phys. 6, 56, 2004). Our results show that it is possible to obtain excellent predictions of the turbulence statistics and the dynamic behavior of the flow with properly trained long-short-term memory (LSTM) networks, leading to relative errors in the mean and the fluctuations below $1\%$. Besides, a newly developed Koopman-based framework, called Koopman with nonlinear forcing (KNF), leads to the same level of accuracy in the statistics at a significantly lower computational expense. Furthermore, the KNF framework outperforms the LSTM network when it comes to short-term predictions. We also observe that using a loss function based only on the instantaneous predictions of the flow can lead to suboptimal predictions in terms of turbulence statistics. Thus, we propose a stopping criterion based on the computed statistics which effectively avoids overfitting to instantaneous predictions at the cost of deteriorated statistics. This suggests that a new loss function, including the averaged behavior of the flow as well as the instantaneous predictions, may lead to an improved generalization ability of the network.