Towards extraction of orthogonal and parsimonious non-linear modes from turbulent flows
Paper and Code
Sep 03, 2021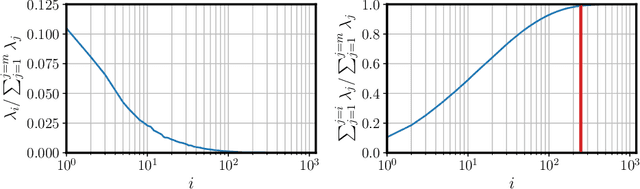



We propose a deep probabilistic-neural-network architecture for learning a minimal and near-orthogonal set of non-linear modes from high-fidelity turbulent-flow-field data useful for flow analysis, reduced-order modeling, and flow control. Our approach is based on $\beta$-variational autoencoders ($\beta$-VAEs) and convolutional neural networks (CNNs), which allow us to extract non-linear modes from multi-scale turbulent flows while encouraging the learning of independent latent variables and penalizing the size of the latent vector. Moreover, we introduce an algorithm for ordering VAE-based modes with respect to their contribution to the reconstruction. We apply this method for non-linear mode decomposition of the turbulent flow through a simplified urban environment, where the flow-field data is obtained based on well-resolved large-eddy simulations (LESs). We demonstrate that by constraining the shape of the latent space, it is possible to motivate the orthogonality and extract a set of parsimonious modes sufficient for high-quality reconstruction. Our results show the excellent performance of the method in the reconstruction against linear-theory-based decompositions. Moreover, we compare our method with available AE-based models. We show the ability of our approach in the extraction of near-orthogonal modes that may lead to interpretability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge