Predicting the wall-shear stress and wall pressure through convolutional neural networks

The objective of this study is to assess the capability of convolution-based neural networks to predict wall quantities in a turbulent open channel flow. The first tests are performed by training a fully-convolutional network (FCN) to predict the 2D velocity-fluctuation fields at the inner-scaled wall-normal location $y^{+}_{\rm target}$, using the sampled velocity fluctuations in wall-parallel planes located farther from the wall, at $y^{+}_{\rm input}$. The predictions from the FCN are compared against the predictions from a proposed R-Net architecture. Since the R-Net model is found to perform better than the FCN model, the former architecture is optimized to predict the 2D streamwise and spanwise wall-shear-stress components and the wall pressure from the sampled velocity-fluctuation fields farther from the wall. The dataset is obtained from DNS of open channel flow at $Re_{\tau} = 180$ and $550$. The turbulent velocity-fluctuation fields are sampled at various inner-scaled wall-normal locations, along with the wall-shear stress and the wall pressure. At $Re_{\tau}=550$, both FCN and R-Net can take advantage of the self-similarity in the logarithmic region of the flow and predict the velocity-fluctuation fields at $y^{+} = 50$ using the velocity-fluctuation fields at $y^{+} = 100$ as input with about 10% error in prediction of streamwise-fluctuations intensity. Further, the R-Net is also able to predict the wall-shear-stress and wall-pressure fields using the velocity-fluctuation fields at $y^+ = 50$ with around 10% error in the intensity of the corresponding fluctuations at both $Re_{\tau} = 180$ and $550$. These results are an encouraging starting point to develop neural-network-based approaches for modelling turbulence near the wall in large-eddy simulations.

Predicting the temporal dynamics of turbulent channels through deep learning

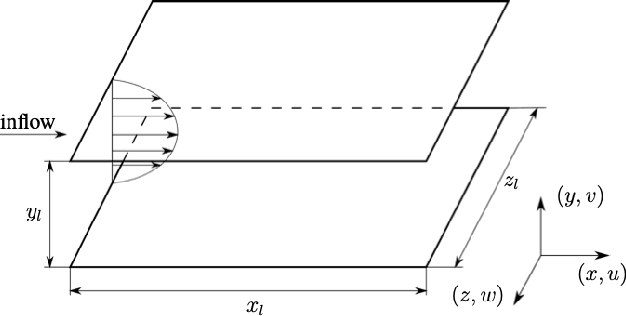
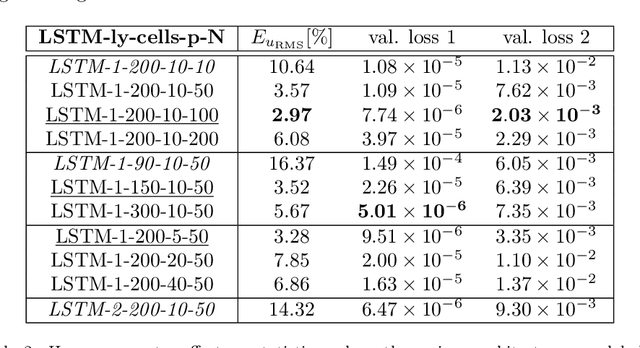
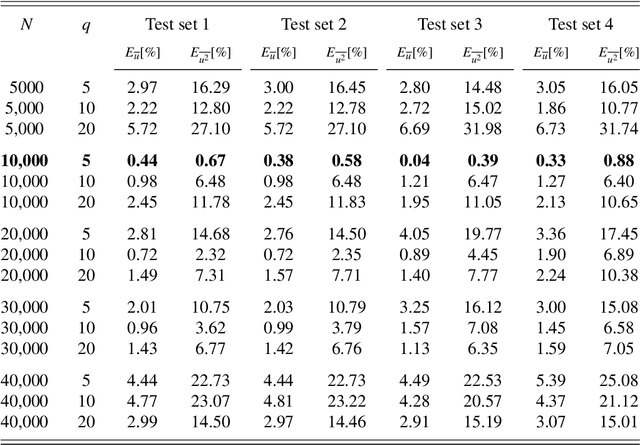
The success of recurrent neural networks (RNNs) has been demonstrated in many applications related to turbulence, including flow control, optimization, turbulent features reproduction as well as turbulence prediction and modeling. With this study we aim to assess the capability of these networks to reproduce the temporal evolution of a minimal turbulent channel flow. We first obtain a data-driven model based on a modal decomposition in the Fourier domain (which we denote as FFT-POD) of the time series sampled from the flow. This particular case of turbulent flow allows us to accurately simulate the most relevant coherent structures close to the wall. Long-short-term-memory (LSTM) networks and a Koopman-based framework (KNF) are trained to predict the temporal dynamics of the minimal-channel-flow modes. Tests with different configurations highlight the limits of the KNF method compared to the LSTM, given the complexity of the flow under study. Long-term prediction for LSTM show excellent agreement from the statistical point of view, with errors below 2% for the best models with respect to the reference. Furthermore, the analysis of the chaotic behaviour through the use of the Lyapunov exponents and of the dynamic behaviour through Poincar\'e maps emphasizes the ability of the LSTM to reproduce the temporal dynamics of turbulence. Alternative reduced-order models (ROMs), based on the identification of different turbulent structures, are explored and they continue to show a good potential in predicting the temporal dynamics of the minimal channel.

Physics-informed neural networks for solving Reynolds-averaged Navier$\unicode{x2013}$Stokes equations

Physics-informed neural networks (PINNs) are successful machine-learning methods for the solution and identification of partial differential equations (PDEs). We employ PINNs for solving the Reynolds-averaged Navier$\unicode{x2013}$Stokes (RANS) equations for incompressible turbulent flows without any specific model or assumption for turbulence, and by taking only the data on the domain boundaries. We first show the applicability of PINNs for solving the Navier$\unicode{x2013}$Stokes equations for laminar flows by solving the Falkner$\unicode{x2013}$Skan boundary layer. We then apply PINNs for the simulation of four turbulent-flow cases, i.e., zero-pressure-gradient boundary layer, adverse-pressure-gradient boundary layer, and turbulent flows over a NACA4412 airfoil and the periodic hill. Our results show the excellent applicability of PINNs for laminar flows with strong pressure gradients, where predictions with less than 1% error can be obtained. For turbulent flows, we also obtain very good accuracy on simulation results even for the Reynolds-stress components.

Recurrent neural networks and Koopman-based frameworks for temporal predictions in turbulence

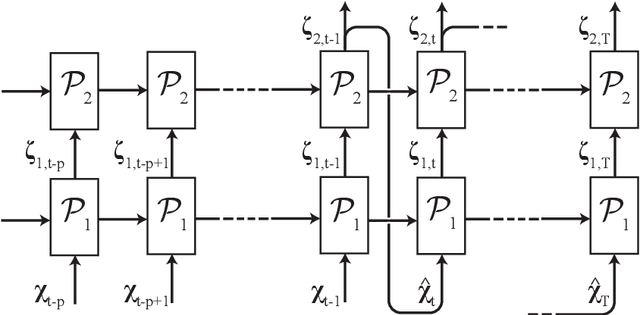
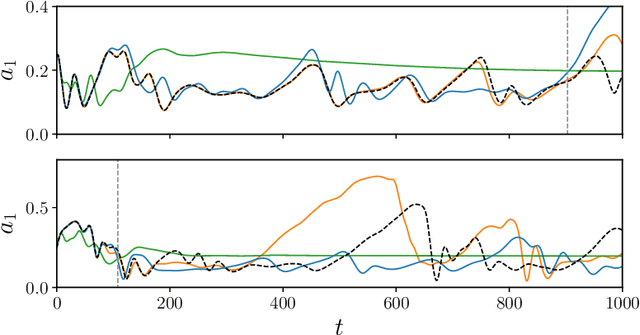
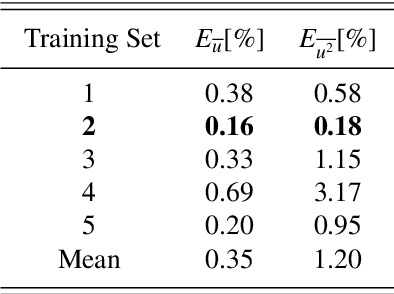
The prediction capabilities of recurrent neural networks and Koopman-based frameworks are assessed in the low-order model of near-wall turbulence by Moehlis et al. (New J. Phys. 6, 56, 2004). Our results show that it is possible to obtain excellent predictions of the turbulence statistics and the dynamic behavior of the flow with properly trained long-short-term memory (LSTM) networks, leading to relative errors in the mean and the fluctuations below $1\%$. Besides, a newly developed Koopman-based framework, called Koopman with nonlinear forcing (KNF), leads to the same level of accuracy in the statistics at a significantly lower computational expense. Furthermore, the KNF framework outperforms the LSTM network when it comes to short-term predictions. We also observe that using a loss function based only on the instantaneous predictions of the flow can lead to suboptimal predictions in terms of turbulence statistics. Thus, we propose a stopping criterion based on the computed statistics which effectively avoids overfitting to instantaneous predictions at the cost of deteriorated statistics. This suggests that a new loss function, including the averaged behavior of the flow as well as the instantaneous predictions, may lead to an improved generalization ability of the network.

On the use of recurrent neural networks for predictions of turbulent flows

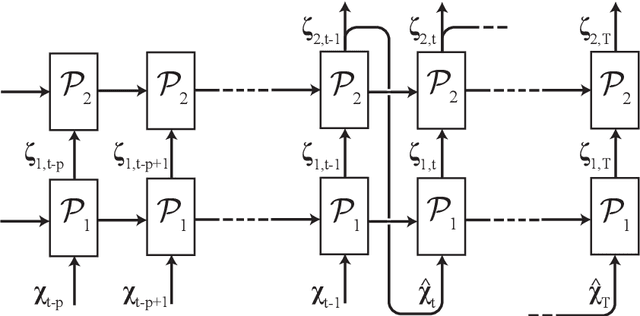
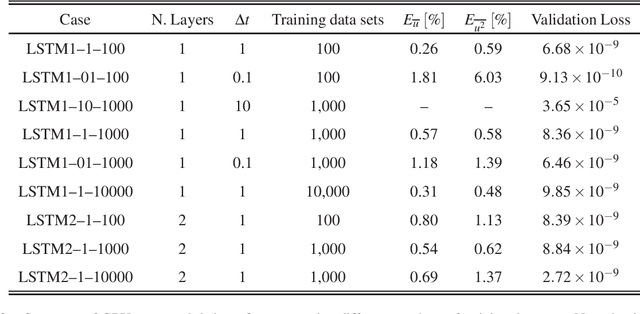
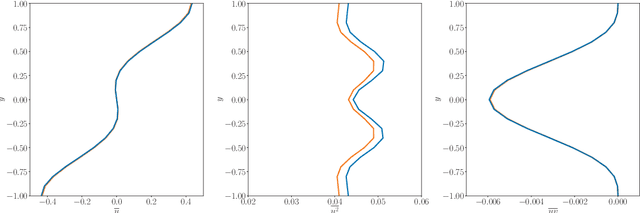
In this paper, the prediction capabilities of recurrent neural networks are assessed in the low-order model of near-wall turbulence by Moehlis {\it et al.} (New J. Phys. {\bf 6}, 56, 2004). Our results show that it is possible to obtain excellent predictions of the turbulence statistics and the dynamic behavior of the flow with properly trained long short-term memory (LSTM) networks, leading to relative errors in the mean and the fluctuations below $1\%$. We also observe that using a loss function based only on the instantaneous predictions of the flow may not lead to the best predictions in terms of turbulence statistics, and it is necessary to define a stopping criterion based on the computed statistics. Furthermore, more sophisticated loss functions, including not only the instantaneous predictions but also the averaged behavior of the flow, may lead to much faster neural network training.