Spiking neural network for nonlinear regression

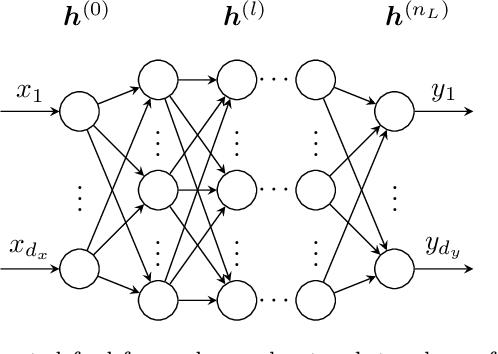
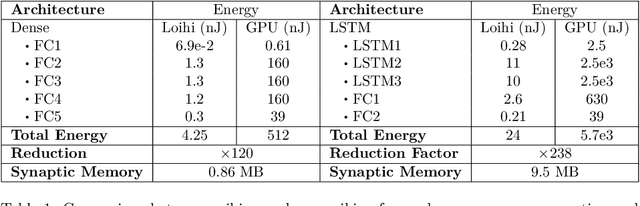
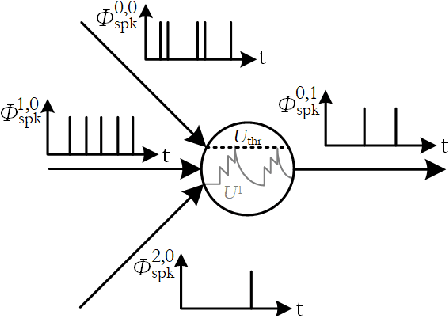
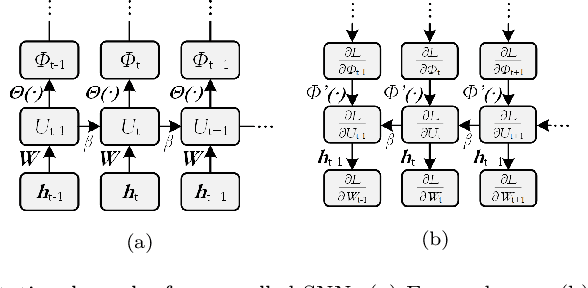
Spiking neural networks, also often referred to as the third generation of neural networks, carry the potential for a massive reduction in memory and energy consumption over traditional, second-generation neural networks. Inspired by the undisputed efficiency of the human brain, they introduce temporal and neuronal sparsity, which can be exploited by next-generation neuromorphic hardware. To open the pathway toward engineering applications, we introduce this exciting technology in the context of continuum mechanics. However, the nature of spiking neural networks poses a challenge for regression problems, which frequently arise in the modeling of engineering sciences. To overcome this problem, a framework for regression using spiking neural networks is proposed. In particular, a network topology for decoding binary spike trains to real numbers is introduced, utilizing the membrane potential of spiking neurons. As the aim of this contribution is a concise introduction to this new methodology, several different spiking neural architectures, ranging from simple spiking feed-forward to complex spiking long short-term memory neural networks, are derived. Several numerical experiments directed towards regression of linear and nonlinear, history-dependent material models are carried out. A direct comparison with counterparts of traditional neural networks shows that the proposed framework is much more efficient while retaining precision and generalizability. All code has been made publicly available in the interest of reproducibility and to promote continued enhancement in this new domain.