Effective Interplay between Sparsity and Quantization: From Theory to Practice

The increasing size of deep neural networks necessitates effective model compression to improve computational efficiency and reduce their memory footprint. Sparsity and quantization are two prominent compression methods that have individually demonstrated significant reduction in computational and memory footprints while preserving model accuracy. While effective, the interplay between these two methods remains an open question. In this paper, we investigate the interaction between these two methods and assess whether their combination impacts final model accuracy. We mathematically prove that applying sparsity before quantization is the optimal sequence for these operations, minimizing error in computation. Our empirical studies across a wide range of models, including OPT and Llama model families (125M-8B) and ViT corroborate these theoretical findings. In addition, through rigorous analysis, we demonstrate that sparsity and quantization are not orthogonal; their interaction can significantly harm model accuracy, with quantization error playing a dominant role in this degradation. Our findings extend to the efficient deployment of large models in resource-limited compute platforms and reduce serving cost, offering insights into best practices for applying these compression methods to maximize efficacy without compromising accuracy.

Multigoal-oriented dual-weighted-residual error estimation using deep neural networks

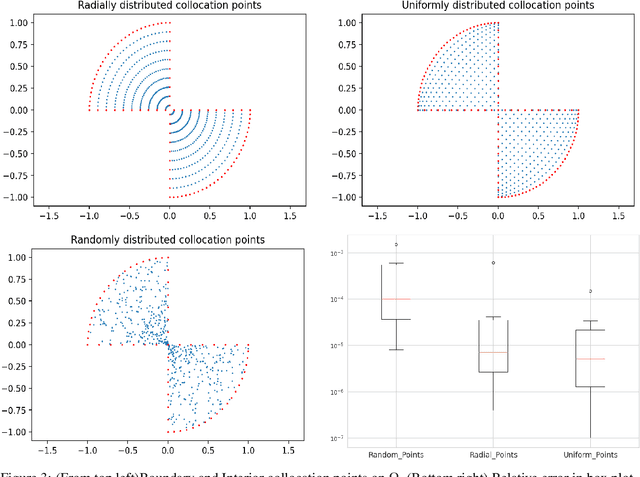
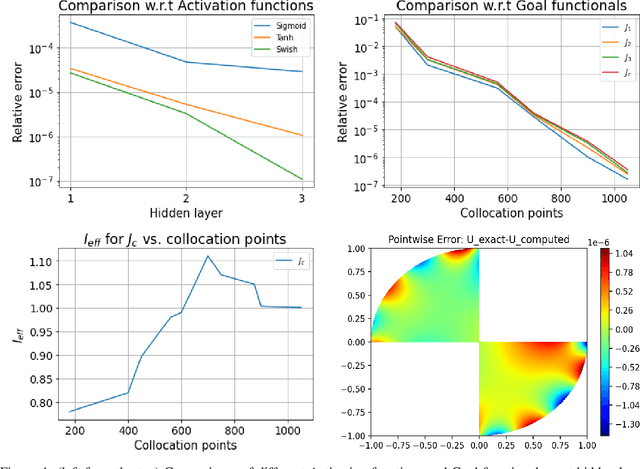
Deep learning has shown successful application in visual recognition and certain artificial intelligence tasks. Deep learning is also considered as a powerful tool with high flexibility to approximate functions. In the present work, functions with desired properties are devised to approximate the solutions of PDEs. Our approach is based on a posteriori error estimation in which the adjoint problem is solved for the error localization to formulate an error estimator within the framework of neural network. An efficient and easy to implement algorithm is developed to obtain a posteriori error estimate for multiple goal functionals by employing the dual-weighted residual approach, which is followed by the computation of both primal and adjoint solutions using the neural network. The present study shows that such a data-driven model based learning has superior approximation of quantities of interest even with relatively less training data. The novel algorithmic developments are substantiated with numerical test examples. The advantages of using deep neural network over the shallow neural network are demonstrated and the convergence enhancing techniques are also presented

Synthesis of Feedback Controller for Nonlinear Control Systems with Optimal Region of Attraction

The problem of computing and characterizing Region of Attraction (ROA) with its many variations have a long tradition in safety-critical systems and control theory. By virtue here comes the connections to Lyapunov functions that are considered as the centerpiece of stability theory for a non linear dynamical systems. The agents may be imperfect because of several limitations in the sensors which ultimately restrict to fully observe the potential adversaries in the environment. Therefore while interacting with human life an autonomous robot should safely explore the outdoor environment by avoiding the dangerous states that may cause physical harm both the systems and environment. In this paper we address this problem and propose a framework of learning policies that adapt to the shape of largest safe region in the state space. At the inception the model is trained to learn an accurate safety certificate for non-linear closed loop dynamics system by constructing Lyapunov Neural Network. The current work is also an extension of the previous work of computing ROA under a fixed policy. Specifically we discuss how to design a state feedback controller by using a typical kind of performance objective function to be optimized and demonstrates our method on a simulated inverted pendulum which clearly shows that how this model can be used to resolve issues of trade-offs and extra design freedom.