Deep Autoencoder based Energy Method for the Bending, Vibration, and Buckling Analysis of Kirchhoff Plates
Paper and Code
Oct 09, 2020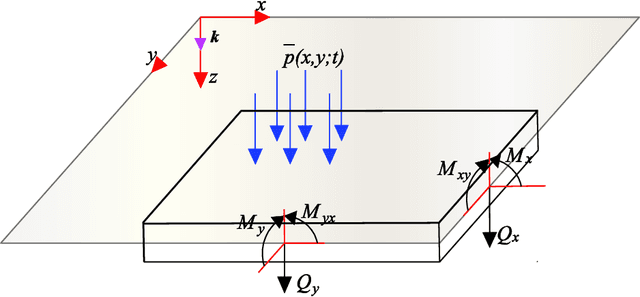

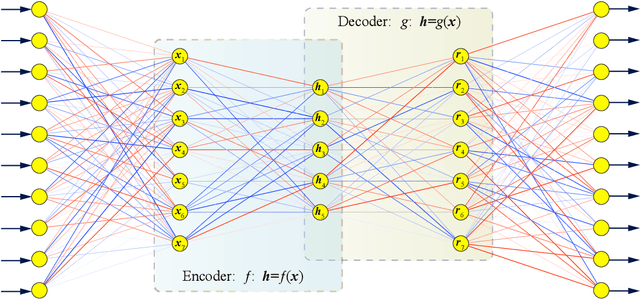

In this paper, we present a deep autoencoder based energy method (DAEM) for the bending, vibration and buckling analysis of Kirchhoff plates. The DAEM exploits the higher order continuity of the DAEM and integrates a deep autoencoder and the minimum total potential principle in one framework yielding an unsupervised feature learning method. The DAEM is a specific type of feedforward deep neural network (DNN) and can also serve as function approximator. With robust feature extraction capacity, the DAEM can more efficiently identify patterns behind the whole energy system, such as the field variables, natural frequency and critical buckling load factor studied in this paper. The objective function is to minimize the total potential energy. The DAEM performs unsupervised learning based on random generated points inside the physical domain so that the total potential energy is minimized at all points. For vibration and buckling analysis, the loss function is constructed based on Rayleigh's principle and the fundamental frequency and the critical buckling load is extracted. A scaled hyperbolic tangent activation function for the underlying mechanical model is presented which meets the continuity requirement and alleviates the gradient vanishing/explosive problems under bending analysis. The DAEM can be easily implemented and we employed the Pytorch library and the LBFGS optimizer. A comprehensive study of the DAEM configuration is performed for several numerical examples with various geometries, load conditions, and boundary conditions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge