Energy-based physics-informed neural network for frictionless contact problems under large deformation

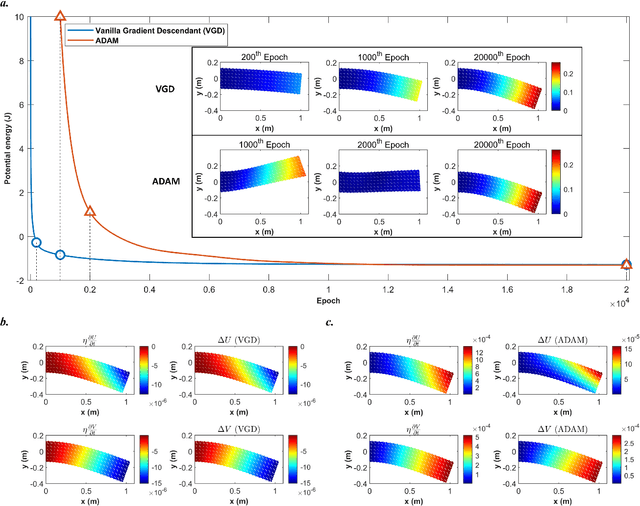
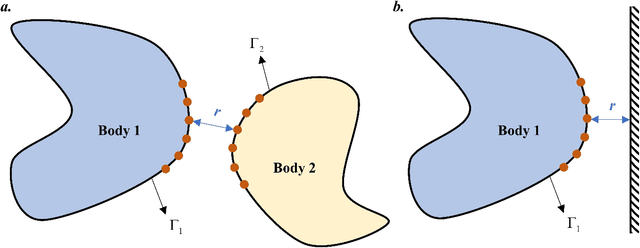
Numerical methods for contact mechanics are of great importance in engineering applications, enabling the prediction and analysis of complex surface interactions under various conditions. In this work, we propose an energy-based physics-informed neural network (PINNs) framework for solving frictionless contact problems under large deformation. Inspired by microscopic Lennard-Jones potential, a surface contact energy is used to describe the contact phenomena. To ensure the robustness of the proposed PINN framework, relaxation, gradual loading and output scaling techniques are introduced. In the numerical examples, the well-known Hertz contact benchmark problem is conducted, demonstrating the effectiveness and robustness of the proposed PINNs framework. Moreover, challenging contact problems with the consideration of geometrical and material nonlinearities are tested. It has been shown that the proposed PINNs framework provides a reliable and powerful tool for nonlinear contact mechanics. More importantly, the proposed PINNs framework exhibits competitive computational efficiency to the commercial FEM software when dealing with those complex contact problems. The codes used in this manuscript are available at https://github.com/JinshuaiBai/energy_PINN_Contact.(The code will be available after acceptance)

Physics-informed radial basis network : A local approximating neural network for solving nonlinear PDEs

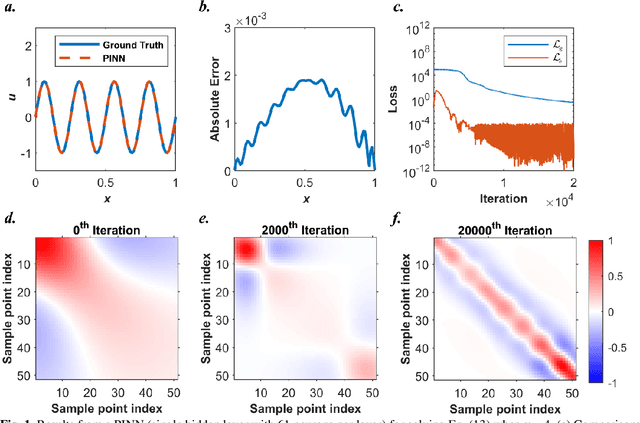
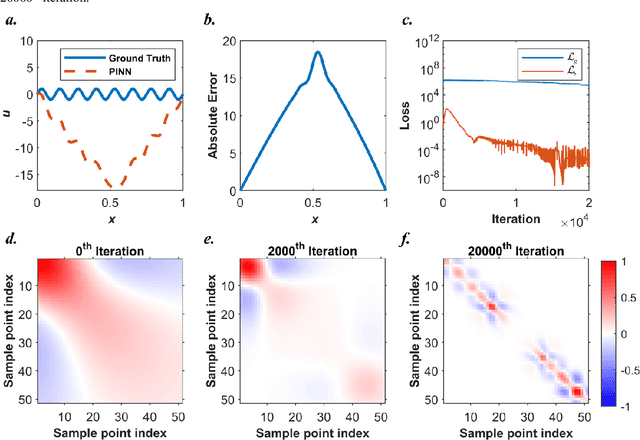
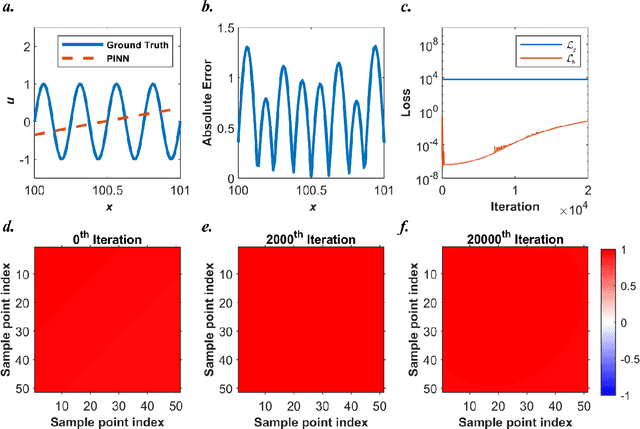
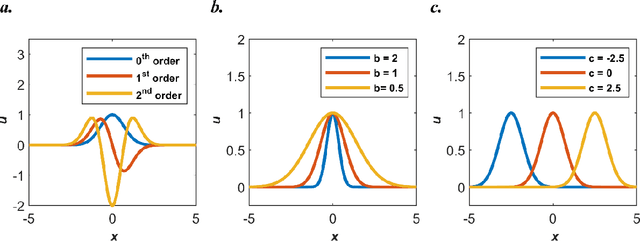
Our recent intensive study has found that physics-informed neural networks (PINN) tend to be local approximators after training. This observation leads to this novel physics-informed radial basis network (PIRBN), which can maintain the local property throughout the entire training process. Compared to deep neural networks, a PIRBN comprises of only one hidden layer and a radial basis "activation" function. Under appropriate conditions, we demonstrated that the training of PIRBNs using gradient descendent methods can converge to Gaussian processes. Besides, we studied the training dynamics of PIRBN via the neural tangent kernel (NTK) theory. In addition, comprehensive investigations regarding the initialisation strategies of PIRBN were conducted. Based on numerical examples, PIRBN has been demonstrated to be more effective and efficient than PINN in solving PDEs with high-frequency features and ill-posed computational domains. Moreover, the existing PINN numerical techniques, such as adaptive learning, decomposition and different types of loss functions, are applicable to PIRBN. The programs that can regenerate all numerical results can be found at https://github.com/JinshuaiBai/PIRBN.