Energy-based physics-informed neural network for frictionless contact problems under large deformation

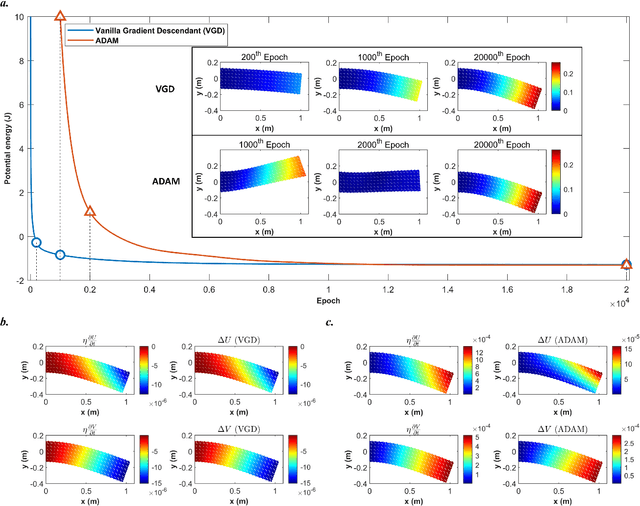
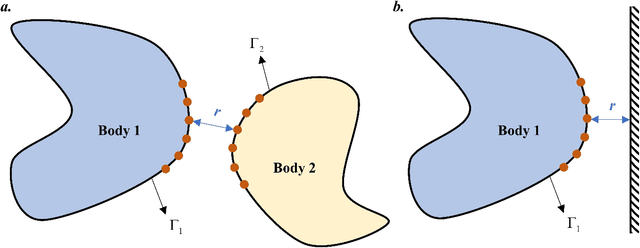
Numerical methods for contact mechanics are of great importance in engineering applications, enabling the prediction and analysis of complex surface interactions under various conditions. In this work, we propose an energy-based physics-informed neural network (PINNs) framework for solving frictionless contact problems under large deformation. Inspired by microscopic Lennard-Jones potential, a surface contact energy is used to describe the contact phenomena. To ensure the robustness of the proposed PINN framework, relaxation, gradual loading and output scaling techniques are introduced. In the numerical examples, the well-known Hertz contact benchmark problem is conducted, demonstrating the effectiveness and robustness of the proposed PINNs framework. Moreover, challenging contact problems with the consideration of geometrical and material nonlinearities are tested. It has been shown that the proposed PINNs framework provides a reliable and powerful tool for nonlinear contact mechanics. More importantly, the proposed PINNs framework exhibits competitive computational efficiency to the commercial FEM software when dealing with those complex contact problems. The codes used in this manuscript are available at https://github.com/JinshuaiBai/energy_PINN_Contact.(The code will be available after acceptance)

Kolmogorov Arnold Informed neural network: A physics-informed deep learning framework for solving PDEs based on Kolmogorov Arnold Networks

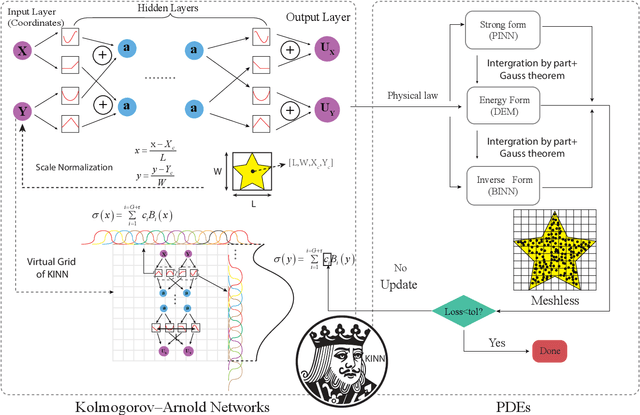
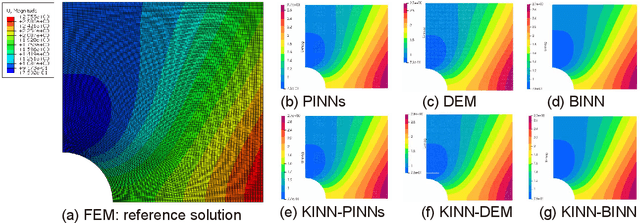
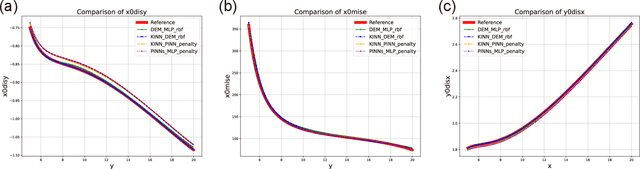
AI for partial differential equations (PDEs) has garnered significant attention, particularly with the emergence of Physics-informed neural networks (PINNs). The recent advent of Kolmogorov-Arnold Network (KAN) indicates that there is potential to revisit and enhance the previously MLP-based PINNs. Compared to MLPs, KANs offer interpretability and require fewer parameters. PDEs can be described in various forms, such as strong form, energy form, and inverse form. While mathematically equivalent, these forms are not computationally equivalent, making the exploration of different PDE formulations significant in computational physics. Thus, we propose different PDE forms based on KAN instead of MLP, termed Kolmogorov-Arnold-Informed Neural Network (KINN). We systematically compare MLP and KAN in various numerical examples of PDEs, including multi-scale, singularity, stress concentration, nonlinear hyperelasticity, heterogeneous, and complex geometry problems. Our results demonstrate that KINN significantly outperforms MLP in terms of accuracy and convergence speed for numerous PDEs in computational solid mechanics, except for the complex geometry problem. This highlights KINN's potential for more efficient and accurate PDE solutions in AI for PDEs.

DCM: Deep complementary energy method based on the principle of minimum complementary energy

The principle of minimum potential and complementary energy are the most important variational principles in solid mechanics. The deep energy method (DEM), which has received much attention, is based on the principle of minimum potential energy, but it lacks the important form of minimum complementary energy. To fill the gap, we propose a deep complementary energy method (DCM) based on the principle of minimum complementary energy. The output function of DCM is the stress function that naturally satisfies the equilibrium equation. We extend the proposed DCM algorithm to DCM-Plus (DCM-P), adding the terms that naturally satisfy the biharmonic equation in the Airy stress function. We combine operator learning with physical equations and propose a deep complementary energy operator method (DCM-O), including branch net, trunk net, basis net, and particular net. DCM-O first combines existing high-fidelity numerical results to train DCM-O through data. Then the complementary energy is used to train the branch net and trunk net in DCM-O. To analyze DCM performance, we present the numerical result of the most common stress functions, the Prandtl and Airy stress function. The proposed method DCM is used to model the representative mechanical problems with different types of boundary conditions. We compare DCM with the existing PINNs and DEM algorithms. The result shows the advantage of the proposed DCM is suitable for dealing with problems of dominated displacement boundary conditions, which is proved by mathematical derivations, as well as with numerical experiments. DCM-P and DCM-O can improve the accuracy and efficiency of DCM. DCM is an essential supplementary energy form to the deep energy method. Operator learning based on the energy method can balance data and physical equations well, giving computational mechanics broad research prospects.

BINN: A deep learning approach for computational mechanics problems based on boundary integral equations

We proposed the boundary-integral type neural networks (BINN) for the boundary value problems in computational mechanics. The boundary integral equations are employed to transfer all the unknowns to the boundary, then the unknowns are approximated using neural networks and solved through a training process. The loss function is chosen as the residuals of the boundary integral equations. Regularization techniques are adopted to efficiently evaluate the weakly singular and Cauchy principle integrals in boundary integral equations. Potential problems and elastostatic problems are mainly concerned in this article as a demonstration. The proposed method has several outstanding advantages: First, the dimensions of the original problem are reduced by one, thus the freedoms are greatly reduced. Second, the proposed method does not require any extra treatment to introduce the boundary conditions, since they are naturally considered through the boundary integral equations. Therefore, the method is suitable for complex geometries. Third, BINN is suitable for problems on the infinite or semi-infinite domains. Moreover, BINN can easily handle heterogeneous problems with a single neural network without domain decomposition.

PETS-SWINF: A regression method that considers images with metadata based Neural Network for pawpularity prediction on 2021 Kaggle Competition "PetFinder.my"

Millions of stray animals suffer on the streets or are euthanized in shelters every day around the world. In order to better adopt stray animals, scoring the pawpularity (cuteness) of stray animals is very important, but evaluating the pawpularity of animals is a very labor-intensive thing. Consequently, there has been an urgent surge of interest to develop an algorithm that scores pawpularity of animals. However, the dataset in Kaggle not only has images, but also metadata describing images. Most methods basically focus on the most advanced image regression methods in recent years, but there is no good method to deal with the metadata of images. To address the above challenges, the paper proposes an image regression model called PETS-SWINF that considers metadata of the images. Our results based on a dataset of Kaggle competition, "PetFinder.my", show that PETS-SWINF has an advantage over only based images models. Our results shows that the RMSE loss of the proposed model on the test dataset is 17.71876 but 17.76449 without metadata. The advantage of the proposed method is that PETS-SWINF can consider both low-order and high-order features of metadata, and adaptively adjust the weights of the image model and the metadata model. The performance is promising as our leadboard score is ranked 15 out of 3545 teams (Gold medal) currently for 2021 Kaggle competition on the challenge "PetFinder.my".

CENN: Conservative energy method based on neural network with subdomains for solving heterogeneous problems involving complex geometries

We propose a conservative energy method based on a neural network with subdomains (CENN), where the admissible function satisfying the essential boundary condition without boundary penalty is constructed by the radial basis function, particular solution neural network, and general neural network. The loss term at the interfaces has the lower order derivative compared to the strong form PINN with subdomains. We apply the proposed method to some representative examples to demonstrate the ability of the proposed method to model strong discontinuity, singularity, complex boundary, non-linear, and heterogeneous PDE problems. The advantage of the method is the efficiency and accuracy compared to the strong form PINN. It is worth emphasizing that the method has a natural advantage in dealing with heterogeneous problems.