Analysis of three dimensional potential problems in non-homogeneous media with deep learning based collocation method

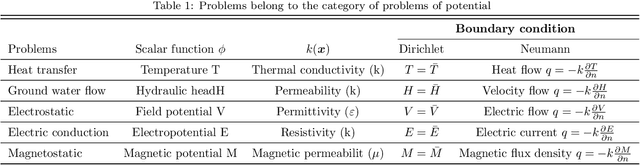
A deep learning based collocation method is presented in this paper to solve the three dimensional potential problems in non-homogeneous media. Based on the universal approximation theorem, the neural network can be utilized to approximate solutions for different PDEs in different geometries. The performance of deep learning based method depends on the configurations of the network and other hyper-parameter settings. This makes the choice of neural network configurations extremely important. The configuration of this deep collocation method is setup by comparing different schemes of smooth activation functions, sampling methods for collocation points generation, combined optimizers. Besides, a convergence proof of this deep collocation method in solving non-homogeneous potential problems is performed. Then the deep collocation method is applied to the analysis of different material variations, and it can be concluded that the deep collocation method predicts the temperature and flux accurately for different material variations, especially the exponential material variations. As a result, the deep learning based collocation method shows a great potential in approximating solutions to PDEs.