Amelie Schafer
Bayesian Physics-Informed Neural Networks for real-world nonlinear dynamical systems
May 12, 2022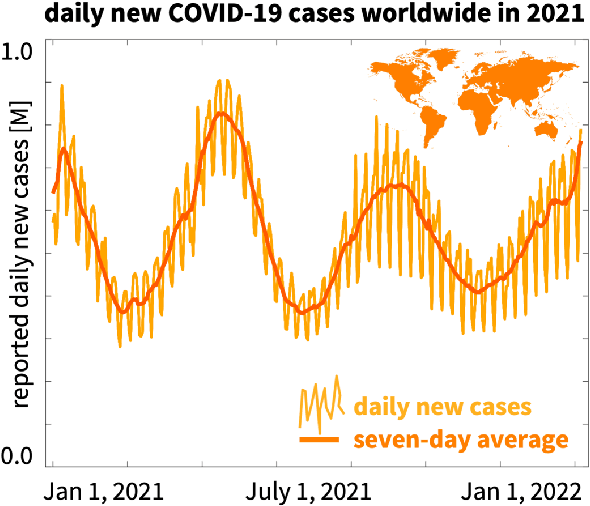
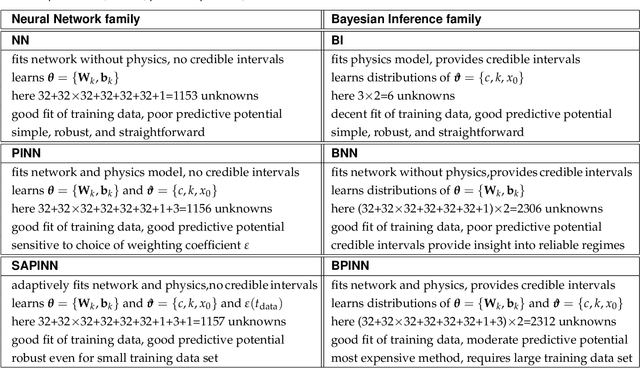

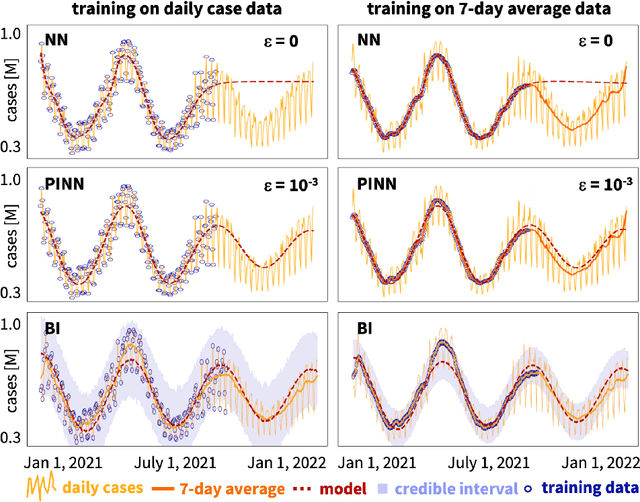
Abstract:Understanding real-world dynamical phenomena remains a challenging task. Across various scientific disciplines, machine learning has advanced as the go-to technology to analyze nonlinear dynamical systems, identify patterns in big data, and make decision around them. Neural networks are now consistently used as universal function approximators for data with underlying mechanisms that are incompletely understood or exceedingly complex. However, neural networks alone ignore the fundamental laws of physics and often fail to make plausible predictions. Here we integrate data, physics, and uncertainties by combining neural networks, physics-informed modeling, and Bayesian inference to improve the predictive potential of traditional neural network models. We embed the physical model of a damped harmonic oscillator into a fully-connected feed-forward neural network to explore a simple and illustrative model system, the outbreak dynamics of COVID-19. Our Physics-Informed Neural Networks can seamlessly integrate data and physics, robustly solve forward and inverse problems, and perform well for both interpolation and extrapolation, even for a small amount of noisy and incomplete data. At only minor additional cost, they can self-adaptively learn the weighting between data and physics. Combined with Bayesian Neural Networks, they can serve as priors in a Bayesian Inference, and provide credible intervals for uncertainty quantification. Our study reveals the inherent advantages and disadvantages of Neural Networks, Bayesian Inference, and a combination of both and provides valuable guidelines for model selection. While we have only demonstrated these approaches for the simple model problem of a seasonal endemic infectious disease, we anticipate that the underlying concepts and trends generalize to more complex disease conditions and, more broadly, to a wide variety of nonlinear dynamical systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge