WarpPINN: Cine-MR image registration with physics-informed neural networks

Heart failure is typically diagnosed with a global function assessment, such as ejection fraction. However, these metrics have low discriminate power, failing to distinguish different types of this disease. Quantifying local deformations in the form of cardiac strain can provide helpful information, but it remains a challenge. In this work, we introduce WarpPINN, a physics-informed neural network to perform image registration to obtain local metrics of the heart deformation. We apply this method to cine magnetic resonance images to estimate the motion during the cardiac cycle. We inform our neural network of near-incompressibility of cardiac tissue by penalizing the jacobian of the deformation field. The loss function has two components: an intensity-based similarity term between the reference and the warped template images, and a regularizer that represents the hyperelastic behavior of the tissue. The architecture of the neural network allows us to easily compute the strain via automatic differentiation to assess cardiac activity. We use Fourier feature mappings to overcome the spectral bias of neural networks, allowing us to capture discontinuities in the strain field. We test our algorithm on a synthetic example and on a cine-MRI benchmark of 15 healthy volunteers. We outperform current methodologies both landmark tracking and strain estimation. We expect that WarpPINN will enable more precise diagnostics of heart failure based on local deformation information. Source code is available at https://github.com/fsahli/WarpPINN.

Multi-fidelity classification using Gaussian processes: accelerating the prediction of large-scale computational models

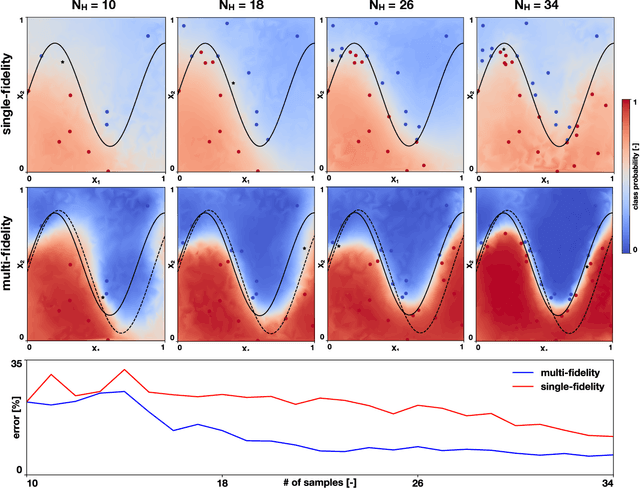
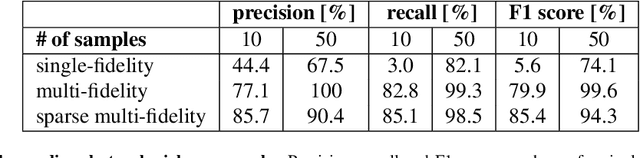
Machine learning techniques typically rely on large datasets to create accurate classifiers. However, there are situations when data is scarce and expensive to acquire. This is the case of studies that rely on state-of-the-art computational models which typically take days to run, thus hindering the potential of machine learning tools. In this work, we present a novel classifier that takes advantage of lower fidelity models and inexpensive approximations to predict the binary output of expensive computer simulations. We postulate an autoregressive model between the different levels of fidelity with Gaussian process priors. We adopt a fully Bayesian treatment for the hyper-parameters and use Markov Chain Mont Carlo samplers. We take advantage of the probabilistic nature of the classifier to implement active learning strategies. We also introduce a sparse approximation to enhance the ability of themulti-fidelity classifier to handle large datasets. We test these multi-fidelity classifiers against their single-fidelity counterpart with synthetic data, showing a median computational cost reduction of 23% for a target accuracy of 90%. In an application to cardiac electrophysiology, the multi-fidelity classifier achieves an F1 score, the harmonic mean of precision and recall, of 99.6% compared to 74.1% of a single-fidelity classifier when both are trained with 50 samples. In general, our results show that the multi-fidelity classifiers outperform their single-fidelity counterpart in terms of accuracy in all cases. We envision that this new tool will enable researchers to study classification problems that would otherwise be prohibitively expensive. Source code is available at https://github.com/fsahli/MFclass.