NeuralUQ: A comprehensive library for uncertainty quantification in neural differential equations and operators

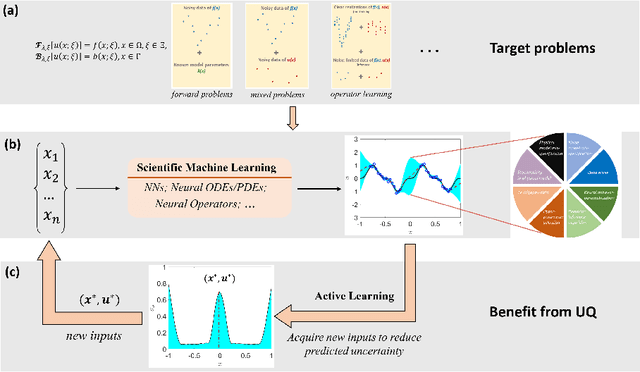
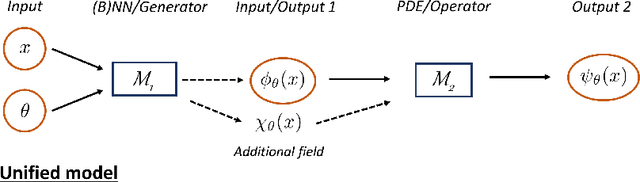
Uncertainty quantification (UQ) in machine learning is currently drawing increasing research interest, driven by the rapid deployment of deep neural networks across different fields, such as computer vision, natural language processing, and the need for reliable tools in risk-sensitive applications. Recently, various machine learning models have also been developed to tackle problems in the field of scientific computing with applications to computational science and engineering (CSE). Physics-informed neural networks and deep operator networks are two such models for solving partial differential equations and learning operator mappings, respectively. In this regard, a comprehensive study of UQ methods tailored specifically for scientific machine learning (SciML) models has been provided in [45]. Nevertheless, and despite their theoretical merit, implementations of these methods are not straightforward, especially in large-scale CSE applications, hindering their broad adoption in both research and industry settings. In this paper, we present an open-source Python library (https://github.com/Crunch-UQ4MI), termed NeuralUQ and accompanied by an educational tutorial, for employing UQ methods for SciML in a convenient and structured manner. The library, designed for both educational and research purposes, supports multiple modern UQ methods and SciML models. It is based on a succinct workflow and facilitates flexible employment and easy extensions by the users. We first present a tutorial of NeuralUQ and subsequently demonstrate its applicability and efficiency in four diverse examples, involving dynamical systems and high-dimensional parametric and time-dependent PDEs.

Uncertainty Quantification in Scientific Machine Learning: Methods, Metrics, and Comparisons

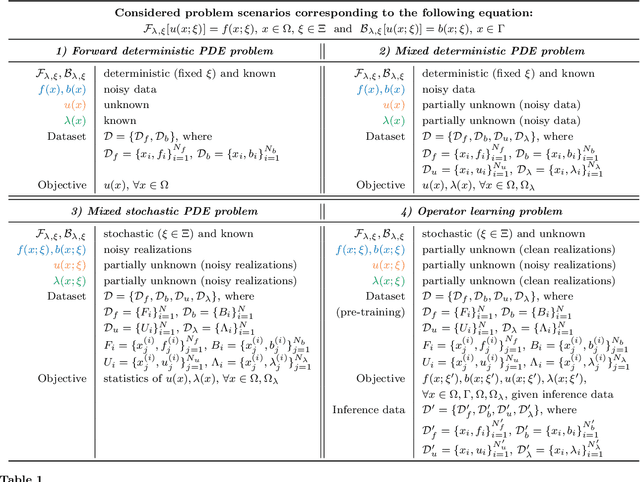
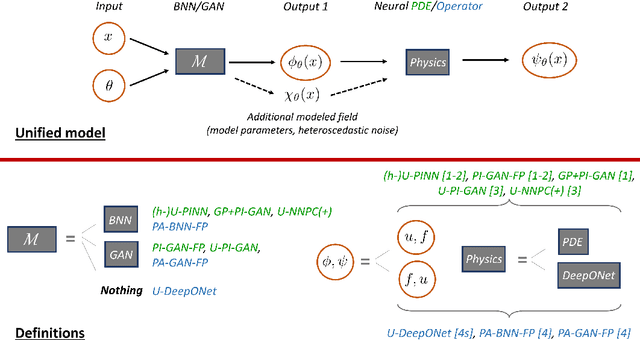
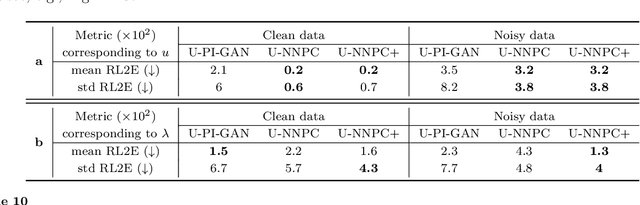
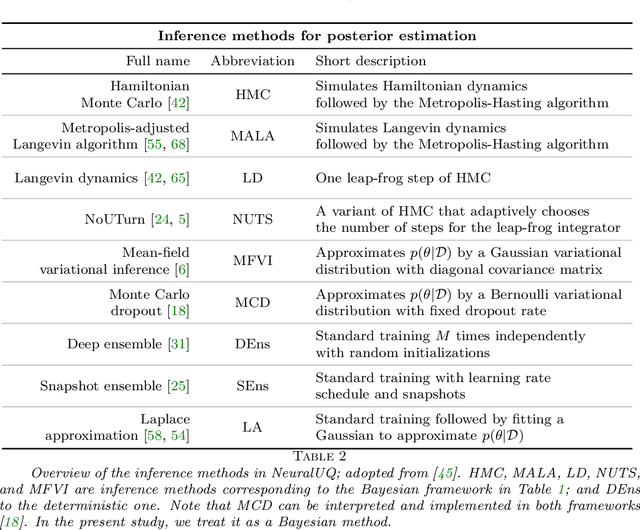
Neural networks (NNs) are currently changing the computational paradigm on how to combine data with mathematical laws in physics and engineering in a profound way, tackling challenging inverse and ill-posed problems not solvable with traditional methods. However, quantifying errors and uncertainties in NN-based inference is more complicated than in traditional methods. This is because in addition to aleatoric uncertainty associated with noisy data, there is also uncertainty due to limited data, but also due to NN hyperparameters, overparametrization, optimization and sampling errors as well as model misspecification. Although there are some recent works on uncertainty quantification (UQ) in NNs, there is no systematic investigation of suitable methods towards quantifying the total uncertainty effectively and efficiently even for function approximation, and there is even less work on solving partial differential equations and learning operator mappings between infinite-dimensional function spaces using NNs. In this work, we present a comprehensive framework that includes uncertainty modeling, new and existing solution methods, as well as evaluation metrics and post-hoc improvement approaches. To demonstrate the applicability and reliability of our framework, we present an extensive comparative study in which various methods are tested on prototype problems, including problems with mixed input-output data, and stochastic problems in high dimensions. In the Appendix, we include a comprehensive description of all the UQ methods employed, which we will make available as open-source library of all codes included in this framework.

Meta-learning PINN loss functions

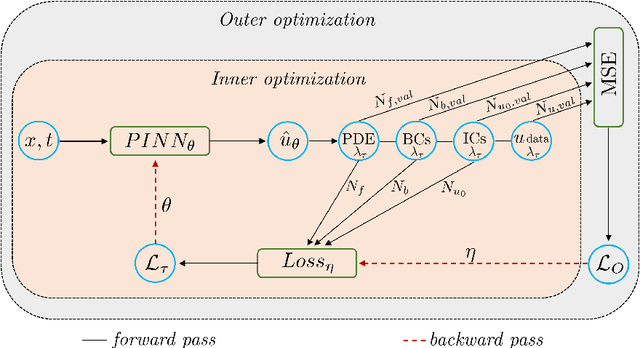
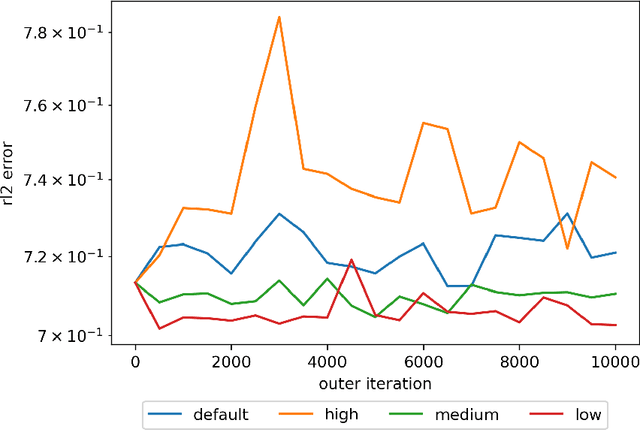
We propose a meta-learning technique for offline discovery of physics-informed neural network (PINN) loss functions. We extend earlier works on meta-learning, and develop a gradient-based meta-learning algorithm for addressing diverse task distributions based on parametrized partial differential equations (PDEs) that are solved with PINNs. Furthermore, based on new theory we identify two desirable properties of meta-learned losses in PINN problems, which we enforce by proposing a new regularization method or using a specific parametrization of the loss function. In the computational examples, the meta-learned losses are employed at test time for addressing regression and PDE task distributions. Our results indicate that significant performance improvement can be achieved by using a shared-among-tasks offline-learned loss function even for out-of-distribution meta-testing. In this case, we solve for test tasks that do not belong to the task distribution used in meta-training, and we also employ PINN architectures that are different from the PINN architecture used in meta-training. To better understand the capabilities and limitations of the proposed method, we consider various parametrizations of the loss function and describe different algorithm design options and how they may affect meta-learning performance.