Meta-learning PINN loss functions
Paper and Code
Jul 12, 2021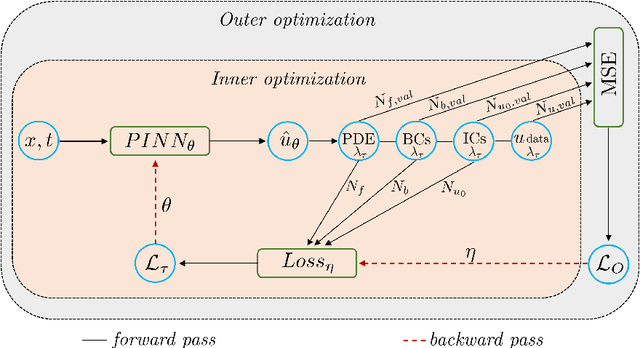

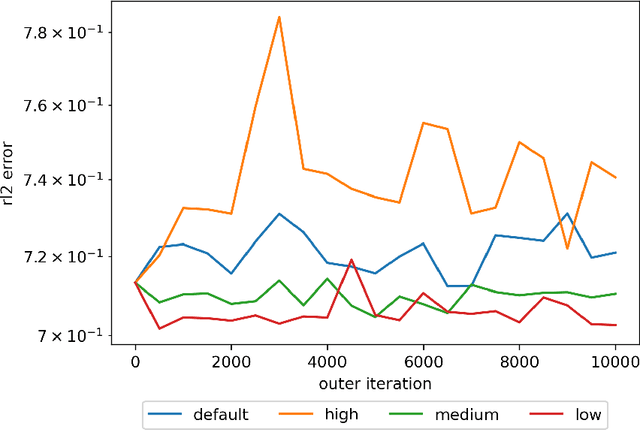
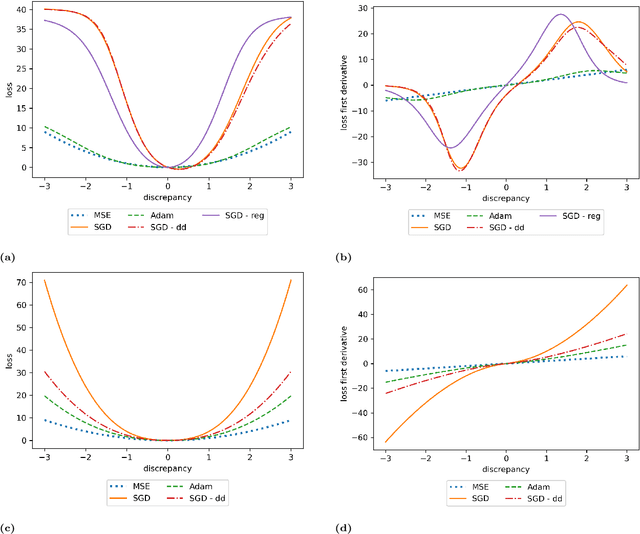
We propose a meta-learning technique for offline discovery of physics-informed neural network (PINN) loss functions. We extend earlier works on meta-learning, and develop a gradient-based meta-learning algorithm for addressing diverse task distributions based on parametrized partial differential equations (PDEs) that are solved with PINNs. Furthermore, based on new theory we identify two desirable properties of meta-learned losses in PINN problems, which we enforce by proposing a new regularization method or using a specific parametrization of the loss function. In the computational examples, the meta-learned losses are employed at test time for addressing regression and PDE task distributions. Our results indicate that significant performance improvement can be achieved by using a shared-among-tasks offline-learned loss function even for out-of-distribution meta-testing. In this case, we solve for test tasks that do not belong to the task distribution used in meta-training, and we also employ PINN architectures that are different from the PINN architecture used in meta-training. To better understand the capabilities and limitations of the proposed method, we consider various parametrizations of the loss function and describe different algorithm design options and how they may affect meta-learning performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge