Physics Informed RNN-DCT Networks for Time-Dependent Partial Differential Equations

Physics-informed neural networks allow models to be trained by physical laws described by general nonlinear partial differential equations. However, traditional architectures struggle to solve more challenging time-dependent problems due to their architectural nature. In this work, we present a novel physics-informed framework for solving time-dependent partial differential equations. Using only the governing differential equations and problem initial and boundary conditions, we generate a latent representation of the problem's spatio-temporal dynamics. Our model utilizes discrete cosine transforms to encode spatial frequencies and recurrent neural networks to process the time evolution. This efficiently and flexibly produces a compressed representation which is used for additional conditioning of physics-informed models. We show experimental results on the Taylor-Green vortex solution to the Navier-Stokes equations. Our proposed model achieves state-of-the-art performance on the Taylor-Green vortex relative to other physics-informed baseline models.

NVIDIA SimNet^{TM}: an AI-accelerated multi-physics simulation framework

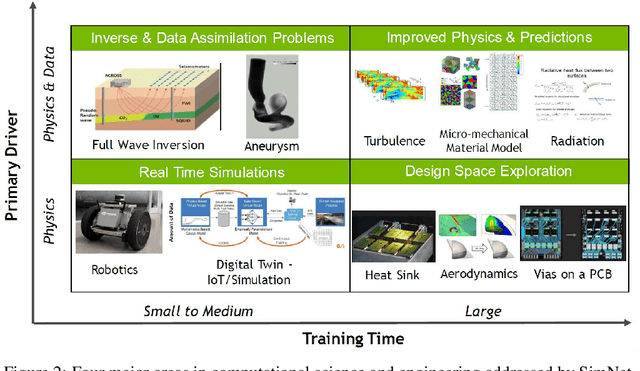
We present SimNet, an AI-driven multi-physics simulation framework, to accelerate simulations across a wide range of disciplines in science and engineering. Compared to traditional numerical solvers, SimNet addresses a wide range of use cases - coupled forward simulations without any training data, inverse and data assimilation problems. SimNet offers fast turnaround time by enabling parameterized system representation that solves for multiple configurations simultaneously, as opposed to the traditional solvers that solve for one configuration at a time. SimNet is integrated with parameterized constructive solid geometry as well as STL modules to generate point clouds. Furthermore, it is customizable with APIs that enable user extensions to geometry, physics and network architecture. It has advanced network architectures that are optimized for high-performance GPU computing, and offers scalable performance for multi-GPU and multi-Node implementation with accelerated linear algebra as well as FP32, FP64 and TF32 computations. In this paper we review the neural network solver methodology, the SimNet architecture, and the various features that are needed for effective solution of the PDEs. We present real-world use cases that range from challenging forward multi-physics simulations with turbulence and complex 3D geometries, to industrial design optimization and inverse problems that are not addressed efficiently by the traditional solvers. Extensive comparisons of SimNet results with open source and commercial solvers show good correlation.

From Deep to Physics-Informed Learning of Turbulence: Diagnostics

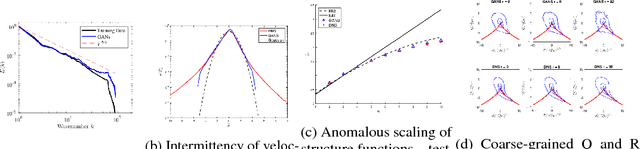
We describe physical tests validating progress made toward acceleration and automation of hydrodynamic codes in the regime of developed turbulence by two {\bf Deep Learning} (DL) Neural Network (NN) schemes trained on {\bf Direct Numerical Simulations} of turbulence. Even the bare DL solutions, which do not take into account any physics of turbulence explicitly, are impressively good overall when it comes to qualitative description of important features of turbulence. However, the early tests have also uncovered some caveats of the DL approaches. We observe that the static DL scheme, implementing Convolutional GAN and trained on spatial snapshots of turbulence, fails to reproduce intermittency of turbulent fluctuations at small scales and details of the turbulence geometry at large scales. We show that the dynamic NN scheme, LAT-NET, trained on a temporal sequence of turbulence snapshots is capable to correct for the small-scale caveat of the static NN. We suggest a path forward towards improving reproducibility of the large-scale geometry of turbulence with NN.

Automated Design using Neural Networks and Gradient Descent

We propose a novel method that makes use of deep neural networks and gradient decent to perform automated design on complex real world engineering tasks. Our approach works by training a neural network to mimic the fitness function of a design optimization task and then, using the differential nature of the neural network, perform gradient decent to maximize the fitness. We demonstrate this methods effectiveness by designing an optimized heat sink and both 2D and 3D airfoils that maximize the lift drag ratio under steady state flow conditions. We highlight that our method has two distinct benefits over other automated design approaches. First, evaluating the neural networks prediction of fitness can be orders of magnitude faster then simulating the system of interest. Second, using gradient decent allows the design space to be searched much more efficiently then other gradient free methods. These two strengths work together to overcome some of the current shortcomings of automated design.

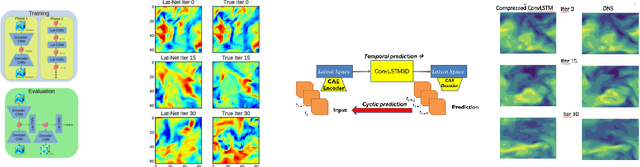
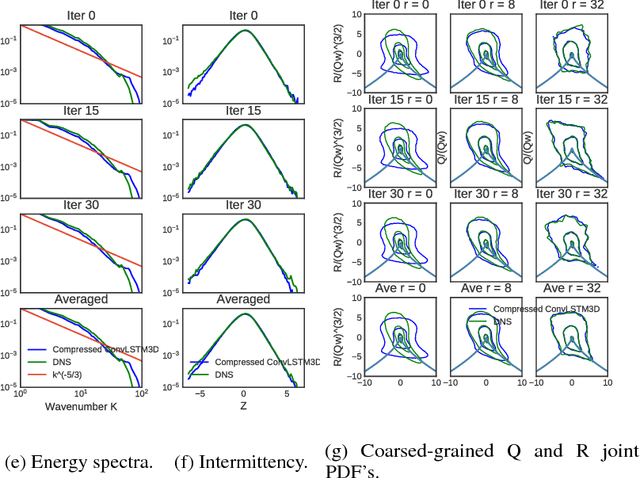
Lat-Net: Compressing Lattice Boltzmann Flow Simulations using Deep Neural Networks

Computational Fluid Dynamics (CFD) is a hugely important subject with applications in almost every engineering field, however, fluid simulations are extremely computationally and memory demanding. Towards this end, we present Lat-Net, a method for compressing both the computation time and memory usage of Lattice Boltzmann flow simulations using deep neural networks. Lat-Net employs convolutional autoencoders and residual connections in a fully differentiable scheme to compress the state size of a simulation and learn the dynamics on this compressed form. The result is a computationally and memory efficient neural network that can be iterated and queried to reproduce a fluid simulation. We show that once Lat-Net is trained, it can generalize to large grid sizes and complex geometries while maintaining accuracy. We also show that Lat-Net is a general method for compressing other Lattice Boltzmann based simulations such as Electromagnetism.