Neuro-symbolic partial differential equation solver

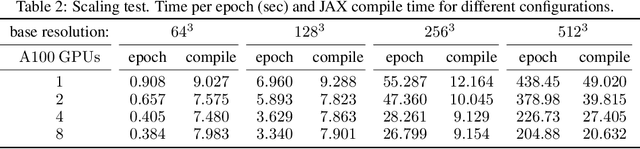
We present a highly scalable strategy for developing mesh-free neuro-symbolic partial differential equation solvers from existing numerical discretizations found in scientific computing. This strategy is unique in that it can be used to efficiently train neural network surrogate models for the solution functions and the differential operators, while retaining the accuracy and convergence properties of state-of-the-art numerical solvers. This neural bootstrapping method is based on minimizing residuals of discretized differential systems on a set of random collocation points with respect to the trainable parameters of the neural network, achieving unprecedented resolution and optimal scaling for solving physical and biological systems.

Physics Informed RNN-DCT Networks for Time-Dependent Partial Differential Equations

Physics-informed neural networks allow models to be trained by physical laws described by general nonlinear partial differential equations. However, traditional architectures struggle to solve more challenging time-dependent problems due to their architectural nature. In this work, we present a novel physics-informed framework for solving time-dependent partial differential equations. Using only the governing differential equations and problem initial and boundary conditions, we generate a latent representation of the problem's spatio-temporal dynamics. Our model utilizes discrete cosine transforms to encode spatial frequencies and recurrent neural networks to process the time evolution. This efficiently and flexibly produces a compressed representation which is used for additional conditioning of physics-informed models. We show experimental results on the Taylor-Green vortex solution to the Navier-Stokes equations. Our proposed model achieves state-of-the-art performance on the Taylor-Green vortex relative to other physics-informed baseline models.

NVIDIA SimNet^{TM}: an AI-accelerated multi-physics simulation framework

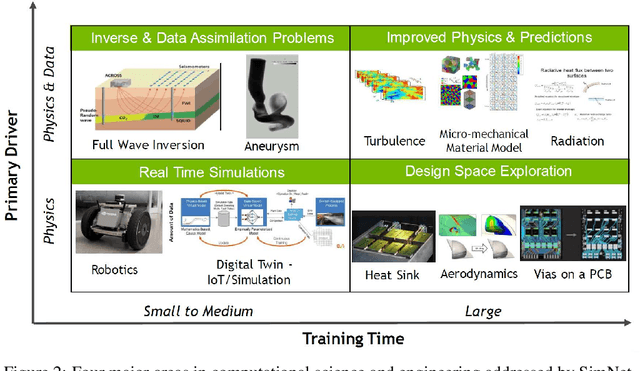
We present SimNet, an AI-driven multi-physics simulation framework, to accelerate simulations across a wide range of disciplines in science and engineering. Compared to traditional numerical solvers, SimNet addresses a wide range of use cases - coupled forward simulations without any training data, inverse and data assimilation problems. SimNet offers fast turnaround time by enabling parameterized system representation that solves for multiple configurations simultaneously, as opposed to the traditional solvers that solve for one configuration at a time. SimNet is integrated with parameterized constructive solid geometry as well as STL modules to generate point clouds. Furthermore, it is customizable with APIs that enable user extensions to geometry, physics and network architecture. It has advanced network architectures that are optimized for high-performance GPU computing, and offers scalable performance for multi-GPU and multi-Node implementation with accelerated linear algebra as well as FP32, FP64 and TF32 computations. In this paper we review the neural network solver methodology, the SimNet architecture, and the various features that are needed for effective solution of the PDEs. We present real-world use cases that range from challenging forward multi-physics simulations with turbulence and complex 3D geometries, to industrial design optimization and inverse problems that are not addressed efficiently by the traditional solvers. Extensive comparisons of SimNet results with open source and commercial solvers show good correlation.