From Noise to Signal: Unveiling Treatment Effects from Digital Health Data through Pharmacology-Informed Neural-SDE

Digital health technologies (DHT), such as wearable devices, provide personalized, continuous, and real-time monitoring of patient. These technologies are contributing to the development of novel therapies and personalized medicine. Gaining insight from these technologies requires appropriate modeling techniques to capture clinically-relevant changes in disease state. The data generated from these devices is characterized by being stochastic in nature, may have missing elements, and exhibits considerable inter-individual variability - thereby making it difficult to analyze using traditional longitudinal modeling techniques. We present a novel pharmacology-informed neural stochastic differential equation (SDE) model capable of addressing these challenges. Using synthetic data, we demonstrate that our approach is effective in identifying treatment effects and learning causal relationships from stochastic data, thereby enabling counterfactual simulation.

Neuro-symbolic partial differential equation solver

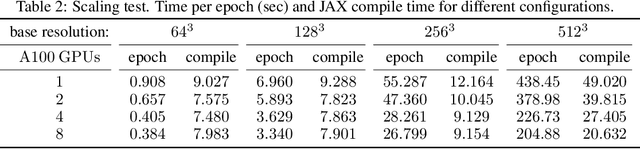
We present a highly scalable strategy for developing mesh-free neuro-symbolic partial differential equation solvers from existing numerical discretizations found in scientific computing. This strategy is unique in that it can be used to efficiently train neural network surrogate models for the solution functions and the differential operators, while retaining the accuracy and convergence properties of state-of-the-art numerical solvers. This neural bootstrapping method is based on minimizing residuals of discretized differential systems on a set of random collocation points with respect to the trainable parameters of the neural network, achieving unprecedented resolution and optimal scaling for solving physical and biological systems.

JAX-DIPS: Neural bootstrapping of finite discretization methods and application to elliptic problems with discontinuities

We present a scalable strategy for development of mesh-free hybrid neuro-symbolic partial differential equation solvers based on existing mesh-based numerical discretization methods. Particularly, this strategy can be used to efficiently train neural network surrogate models for the solution functions and operators of partial differential equations while retaining the accuracy and convergence properties of the state-of-the-art numerical solvers. The presented neural bootstrapping method (hereby dubbed NBM) is based on evaluation of the finite discretization residuals of the PDE system obtained on implicit Cartesian cells centered on a set of random collocation points with respect to trainable parameters of the neural network. We apply NBM to the important class of elliptic problems with jump conditions across irregular interfaces in three spatial dimensions. We show the method is convergent such that model accuracy improves by increasing number of collocation points in the domain. The algorithms presented here are implemented and released in a software package named JAX-DIPS (https://github.com/JAX-DIPS/JAX-DIPS), standing for differentiable interfacial PDE solver. JAX-DIPS is purely developed in JAX, offering end-to-end differentiability from mesh generation to the higher level discretization abstractions, geometric integrations, and interpolations, thus facilitating research into use of differentiable algorithms for developing hybrid PDE solvers.

Solving inverse-PDE problems with physics-aware neural networks

We propose a novel composite framework that enables finding unknown fields in the context of inverse problems for partial differential equations (PDEs). We blend the high expressibility of deep neural networks as universal function estimators with the accuracy and reliability of existing numerical algorithms for partial differential equations. Our design brings together techniques of computational mathematics, machine learning and pattern recognition under one umbrella to seamlessly incorporate any domain-specific knowledge and insights through modeling. The network is explicitly aware of the governing physics through a hard-coded PDE solver stage; this subsequently focuses the computational load to only the discovery of the hidden fields. In addition, techniques of pattern recognition and surface reconstruction are used to further represent the unknown fields in a straightforward fashion. Most importantly, our inverse-PDE solver allows effortless integration of domain-specific knowledge about the physics of underlying fields, such as symmetries and proper basis functions. We call this approach Blended Inverse-PDE Networks (hereby dubbed BIPDE-Nets) and demonstrate its applicability on recovering the variable diffusion coefficient in Poisson problems in one and two spatial dimensions. We also show that this approach is robust to noise.