Preference optimization of protein language models as a multi-objective binder design paradigm

We present a multi-objective binder design paradigm based on instruction fine-tuning and direct preference optimization (DPO) of autoregressive protein language models (pLMs). Multiple design objectives are encoded in the language model through direct optimization on expert curated preference sequence datasets comprising preferred and dispreferred distributions. We show the proposed alignment strategy enables ProtGPT2 to effectively design binders conditioned on specified receptors and a drug developability criterion. Generated binder samples demonstrate median isoelectric point (pI) improvements by $17\%-60\%$.

Neuro-symbolic partial differential equation solver

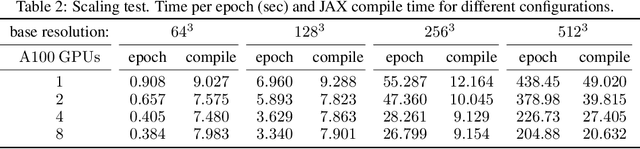
We present a highly scalable strategy for developing mesh-free neuro-symbolic partial differential equation solvers from existing numerical discretizations found in scientific computing. This strategy is unique in that it can be used to efficiently train neural network surrogate models for the solution functions and the differential operators, while retaining the accuracy and convergence properties of state-of-the-art numerical solvers. This neural bootstrapping method is based on minimizing residuals of discretized differential systems on a set of random collocation points with respect to the trainable parameters of the neural network, achieving unprecedented resolution and optimal scaling for solving physical and biological systems.

JAX-DIPS: Neural bootstrapping of finite discretization methods and application to elliptic problems with discontinuities

We present a scalable strategy for development of mesh-free hybrid neuro-symbolic partial differential equation solvers based on existing mesh-based numerical discretization methods. Particularly, this strategy can be used to efficiently train neural network surrogate models for the solution functions and operators of partial differential equations while retaining the accuracy and convergence properties of the state-of-the-art numerical solvers. The presented neural bootstrapping method (hereby dubbed NBM) is based on evaluation of the finite discretization residuals of the PDE system obtained on implicit Cartesian cells centered on a set of random collocation points with respect to trainable parameters of the neural network. We apply NBM to the important class of elliptic problems with jump conditions across irregular interfaces in three spatial dimensions. We show the method is convergent such that model accuracy improves by increasing number of collocation points in the domain. The algorithms presented here are implemented and released in a software package named JAX-DIPS (https://github.com/JAX-DIPS/JAX-DIPS), standing for differentiable interfacial PDE solver. JAX-DIPS is purely developed in JAX, offering end-to-end differentiability from mesh generation to the higher level discretization abstractions, geometric integrations, and interpolations, thus facilitating research into use of differentiable algorithms for developing hybrid PDE solvers.