From Noise to Signal: Unveiling Treatment Effects from Digital Health Data through Pharmacology-Informed Neural-SDE

Digital health technologies (DHT), such as wearable devices, provide personalized, continuous, and real-time monitoring of patient. These technologies are contributing to the development of novel therapies and personalized medicine. Gaining insight from these technologies requires appropriate modeling techniques to capture clinically-relevant changes in disease state. The data generated from these devices is characterized by being stochastic in nature, may have missing elements, and exhibits considerable inter-individual variability - thereby making it difficult to analyze using traditional longitudinal modeling techniques. We present a novel pharmacology-informed neural stochastic differential equation (SDE) model capable of addressing these challenges. Using synthetic data, we demonstrate that our approach is effective in identifying treatment effects and learning causal relationships from stochastic data, thereby enabling counterfactual simulation.

Integration of Graph Neural Network and Neural-ODEs for Tumor Dynamic Prediction

In anti-cancer drug development, a major scientific challenge is disentangling the complex relationships between high-dimensional genomics data from patient tumor samples, the corresponding tumor's organ of origin, the drug targets associated with given treatments and the resulting treatment response. Furthermore, to realize the aspirations of precision medicine in identifying and adjusting treatments for patients depending on the therapeutic response, there is a need for building tumor dynamic models that can integrate both longitudinal tumor size as well as multimodal, high-content data. In this work, we take a step towards enhancing personalized tumor dynamic predictions by proposing a heterogeneous graph encoder that utilizes a bipartite Graph Convolutional Neural network (GCN) combined with Neural Ordinary Differential Equations (Neural-ODEs). We applied the methodology to a large collection of patient-derived xenograft (PDX) data, spanning a wide variety of treatments (as well as their combinations) on tumors that originated from a number of different organs. We first show that the methodology is able to discover a tumor dynamic model that significantly improves upon an empirical model which is in current use. Additionally, we show that the graph encoder is able to effectively utilize multimodal data to enhance tumor predictions. Our findings indicate that the methodology holds significant promise and offers potential applications in pre-clinical settings.

Explainable Deep Learning for Tumor Dynamic Modeling and Overall Survival Prediction using Neural-ODE

While tumor dynamic modeling has been widely applied to support the development of oncology drugs, there remains a need to increase predictivity, enable personalized therapy, and improve decision-making. We propose the use of Tumor Dynamic Neural-ODE (TDNODE) as a pharmacology-informed neural network to enable model discovery from longitudinal tumor size data. We show that TDNODE overcomes a key limitation of existing models in its ability to make unbiased predictions from truncated data. The encoder-decoder architecture is designed to express an underlying dynamical law which possesses the fundamental property of generalized homogeneity with respect to time. Thus, the modeling formalism enables the encoder output to be interpreted as kinetic rate metrics, with inverse time as the physical unit. We show that the generated metrics can be used to predict patients' overall survival (OS) with high accuracy. The proposed modeling formalism provides a principled way to integrate multimodal dynamical datasets in oncology disease modeling.

Computing the Hazard Ratios Associated with Explanatory Variables Using Machine Learning Models of Survival Data

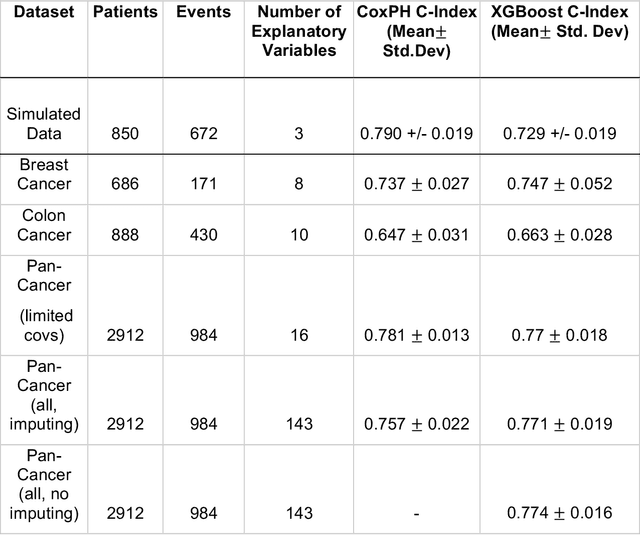
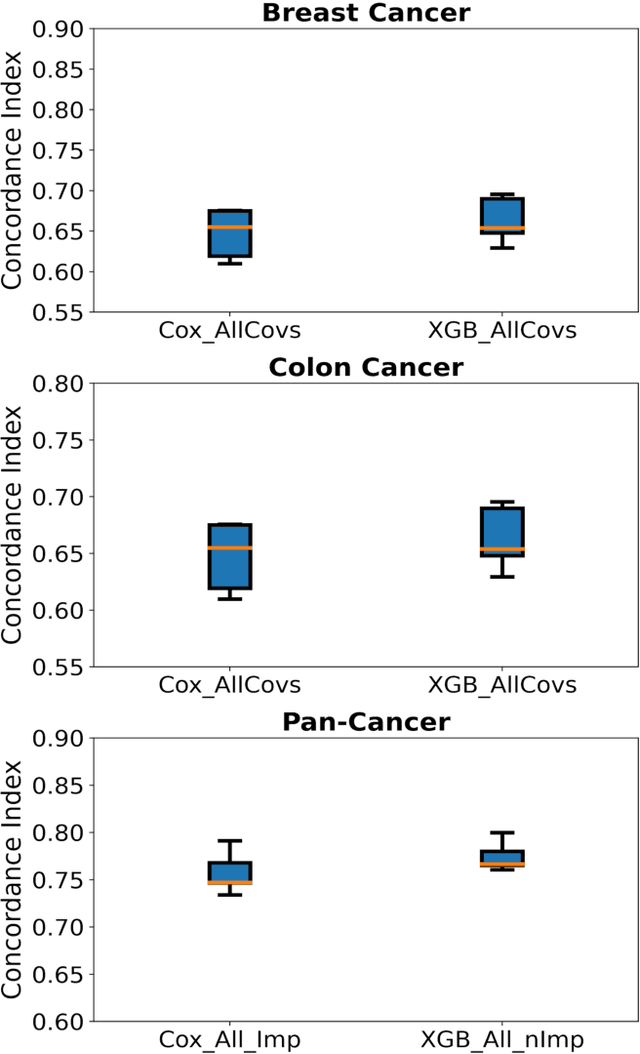
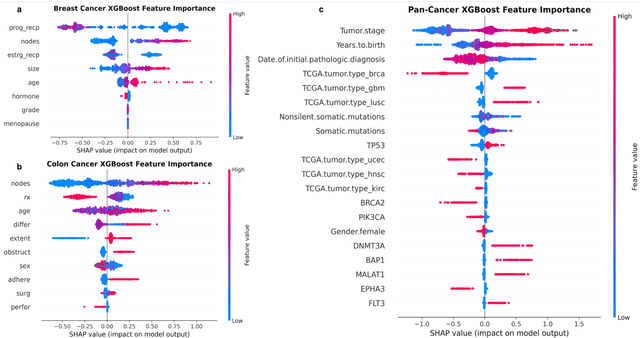
Purpose: The application of Cox Proportional Hazards (CoxPH) models to survival data and the derivation of Hazard Ratio (HR) is well established. While nonlinear, tree-based Machine Learning (ML) models have been developed and applied to the survival analysis, no methodology exists for computing HRs associated with explanatory variables from such models. We describe a novel way to compute HRs from tree-based ML models using the Shapley additive explanation (SHAP) values, which is a locally accurate and consistent methodology to quantify explanatory variables' contribution to predictions. Methods: We used three sets of publicly available survival data consisting of patients with colon, breast or pan cancer and compared the performance of CoxPH to the state-of-art ML model, XGBoost. To compute the HR for explanatory variables from the XGBoost model, the SHAP values were exponentiated and the ratio of the means over the two subgroups calculated. The confidence interval was computed via bootstrapping the training data and generating the ML model 1000 times. Across the three data sets, we systematically compared HRs for all explanatory variables. Open-source libraries in Python and R were used in the analyses. Results: For the colon and breast cancer data sets, the performance of CoxPH and XGBoost were comparable and we showed good consistency in the computed HRs. In the pan-cancer dataset, we showed agreement in most variables but also an opposite finding in two of the explanatory variables between the CoxPH and XGBoost result. Subsequent Kaplan-Meier plots supported the finding of the XGBoost model. Conclusion: Enabling the derivation of HR from ML models can help to improve the identification of risk factors from complex survival datasets and enhance the prediction of clinical trial outcomes.

Deep learning prediction of patient response time course from early data via neural-pharmacokinetic/pharmacodynamic modeling

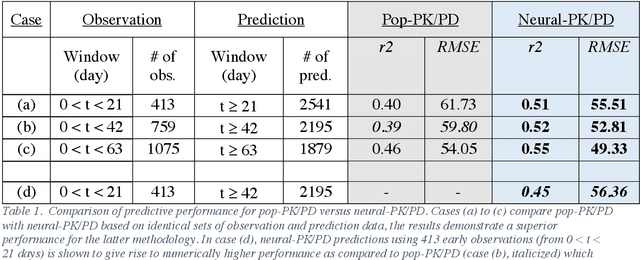
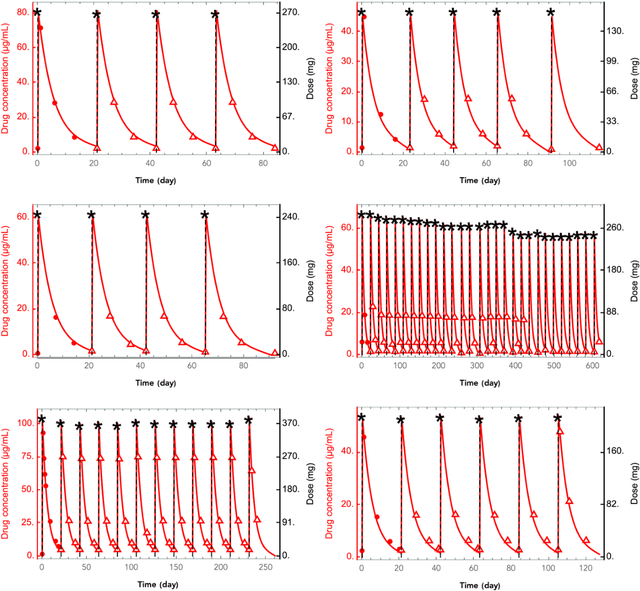
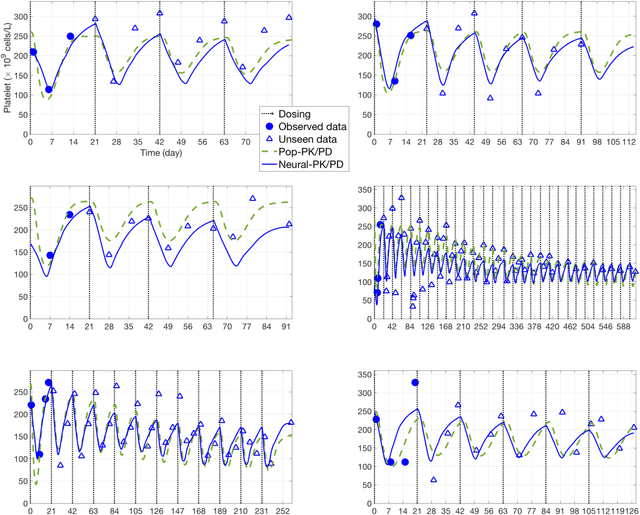
The longitudinal analysis of patient response time course following doses of therapeutics is currently performed using Pharmacokinetic/Pharmacodynamic (PK/PD) methodologies, which requires significant human experience and expertise in the modeling of dynamical systems. By utilizing recent advancements in deep learning, we show that the governing differential equations can be learnt directly from longitudinal patient data. In particular, we propose a novel neural-PK/PD framework that combines key pharmacological principles with neural ordinary differential equations. We applied it to an analysis of drug concentration and platelet response from a clinical dataset consisting of over 600 patients. We show that the neural-PK/PD model improves upon a state-of-the-art model with respect to metrics for temporal prediction. Furthermore, by incorporating key PK/PD concepts into its architecture, the model can generalize and enable the simulations of patient responses to untested dosing regimens. These results demonstrate the potential of neural-PK/PD for automated predictive analytics of patient response time course.