Physics-Informed Regularization of Deep Neural Networks

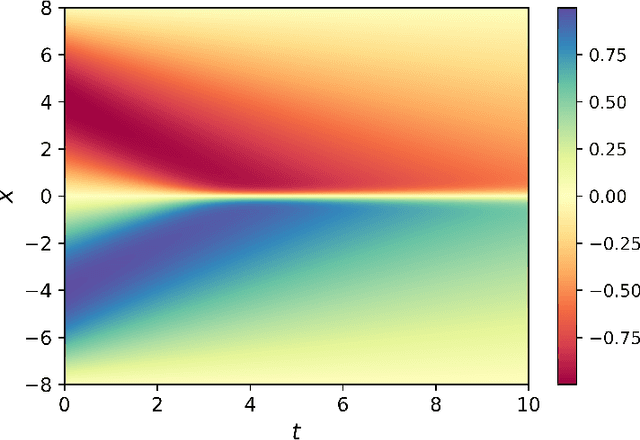
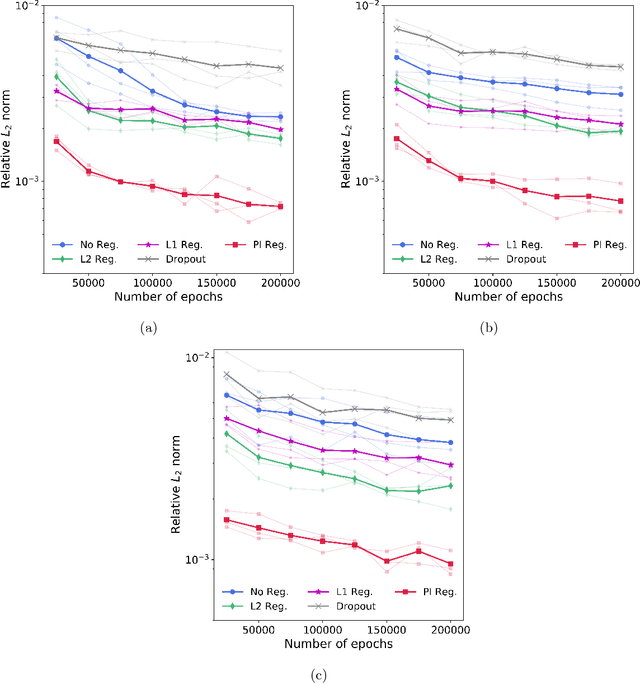
This paper presents a novel physics-informed regularization method for training of deep neural networks (DNNs). In particular, we focus on the DNN representation for the response of a physical or biological system, for which a set of governing laws are known. These laws often appear in the form of differential equations, derived from first principles, empirically-validated laws, and/or domain expertise. We propose a DNN training approach that utilizes these known differential equations in addition to the measurement data, by introducing a penalty term to the training loss function to penalize divergence form the governing laws. Through three numerical examples, we will show that the proposed regularization produces surrogates that are physically interpretable with smaller generalization errors, when compared to other common regularization methods.