A Deep Neural Network Surrogate for High-Dimensional Random Partial Differential Equations
Paper and Code
Aug 24, 2018
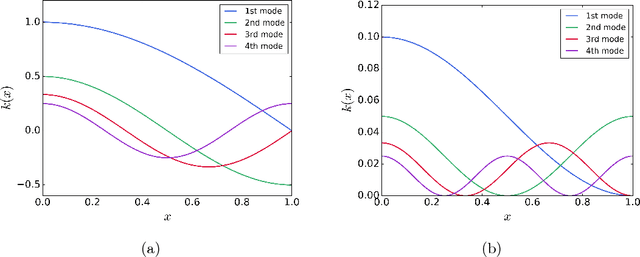
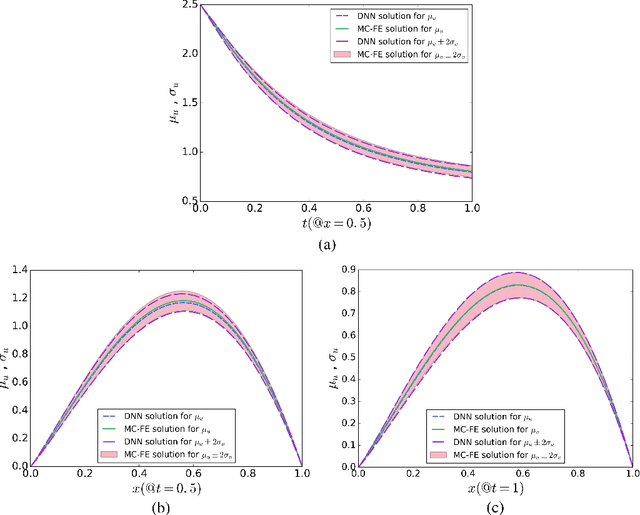
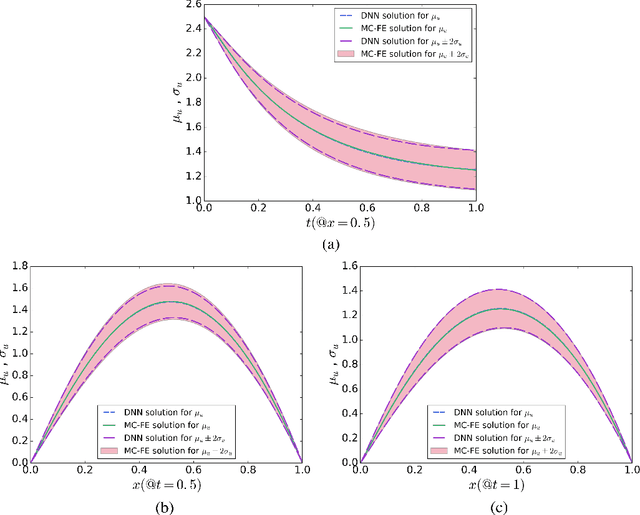
Developing efficient numerical algorithms for the solution of high dimensional random Partial Differential Equations (PDEs) has been a challenging task due to the well-known curse of dimensionality. We present a new solution framework for these problems based on a deep learning approach. Specifically, the random PDE is approximated by a feed-forward fully-connected deep residual network, with either strong or weak enforcement of initial and boundary constraints. The framework is mesh-free, and can handle irregular computational domains. Parameters of the approximating deep neural network are determined iteratively using variants of the Stochastic Gradient Descent (SGD) algorithm. The satisfactory accuracy of the proposed frameworks is numerically demonstrated on diffusion and heat conduction problems, in comparison with the converged Monte Carlo-based finite element results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge