Deep Learning and Spectral Embedding for Graph Partitioning
Paper and Code
Oct 16, 2021

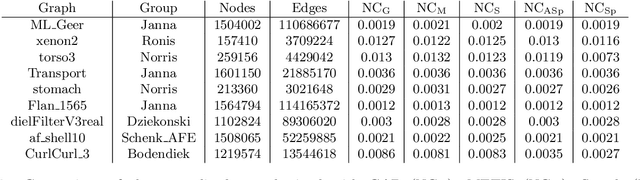

We present a graph bisection and partitioning algorithm based on graph neural networks. For each node in the graph, the network outputs probabilities for each of the partitions. The graph neural network consists of two modules: an embedding phase and a partitioning phase. The embedding phase is trained first by minimizing a loss function inspired by spectral graph theory. The partitioning module is trained through a loss function that corresponds to the expected value of the normalized cut. Both parts of the neural network rely on SAGE convolutional layers and graph coarsening using heavy edge matching. The multilevel structure of the neural network is inspired by the multigrid algorithm. Our approach generalizes very well to bigger graphs and has partition quality comparable to METIS, Scotch and spectral partitioning, with shorter runtime compared to METIS and spectral partitioning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge