Formulations and scalability of neural network surrogates in nonlinear optimization problems
Paper and Code
Dec 16, 2024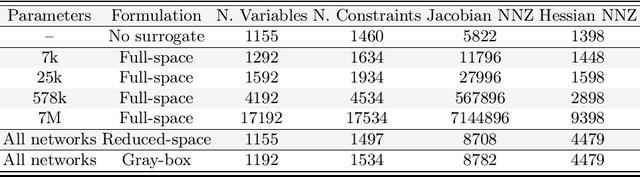
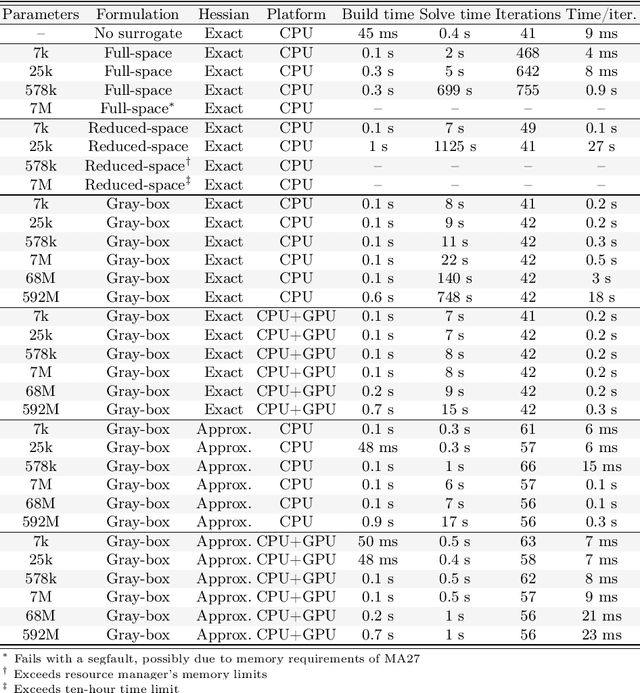
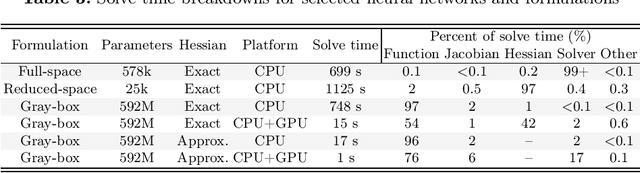
We compare full-space, reduced-space, and gray-box formulations for representing trained neural networks in nonlinear constrained optimization problems. We test these formulations on a transient stability-constrained, security-constrained alternating current optimal power flow (SCOPF) problem where the transient stability criteria are represented by a trained neural network surrogate. Optimization problems are implemented in JuMP and trained neural networks are embedded using a new Julia package: MathOptAI.jl. To study the bottlenecks of the three formulations, we use neural networks with up to 590 million trained parameters. The full-space formulation is bottlenecked by the linear solver used by the optimization algorithm, while the reduced-space formulation is bottlenecked by the algebraic modeling environment and derivative computations. The gray-box formulation is the most scalable and is capable of solving with the largest neural networks tested. It is bottlenecked by evaluation of the neural network's outputs and their derivatives, which may be accelerated with a graphics processing unit (GPU). Leveraging the gray-box formulation and GPU acceleration, we solve our test problem with our largest neural network surrogate in 2.5$\times$ the time required for a simpler SCOPF problem without the stability constraint.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge