Environment-Conditioned Diffusion Meta-Learning for Data-Efficient WiFi Localization

Fingerprinting-based localization often suffers from poor cross-environment generalization, especially when only a few labeled samples are available in the target environment. Existing methods mitigate distribution shifts through domain adaptation or improved signal representations, but they usually ignore environmental geometry or use it in a deterministic manner, limiting their ability to capture diverse multipath variations in complex propagation conditions. To address this issue, we propose EnvCoLoc, an environment-conditioned diffusion meta-learning framework for few-shot fingerprinting localization. EnvCoLoc extracts structured descriptors from 3D point clouds and uses them to condition a latent diffusion generator, which produces environment-specific parameter offsets to modulate a shared meta-learned initialization. This design injects geometry-aware priors into the adaptation process and provides more informative initializations for new environments. To learn the stochastic mapping from coarse environmental descriptors to high-dimensional parameter corrections under limited data, the diffusion generator and localization network are jointly optimized within a two-loop meta-learning framework. The generated offsets capture systematic environment-dependent variations, while gradient-based inner-loop adaptation further refines the model to reduce residual task-specific mismatch. We also provide an excess-loss analysis for finite-step adaptation, theoretically supporting the benefit of geometry-aware initialization. Real-world experiments show that EnvCoLoc consistently improves localization accuracy over baseline methods, achieving up to a 20.0% reduction in mean localization error in NLOS scenarios with only 10 support samples.

Movable-Antenna Enabled Robust Vehicular Consumer Networks Under Imperfect CSI

The accelerating advancement of intelligent transportation systems has established consumer-oriented vehicular networks (CVNs) as a critical infrastructure for next-generation connected mobility. However, the high mobility of vehicular users (VUs) introduces significant channel state information (CSI) uncertainty, which severely undermines the performance of conventional fixed-position antenna systems. To address this, this paper explores the deployment of movable-antennas (MAs) to enhance communication robustness in CVNs under imperfect CSI conditions. We develop a joint optimization framework that dynamically coordinates the spatial positioning of MAs and transmit beamforming at the base station, with the objective of maximizing the worst-case sum rate across all VUs. The problem is formulated as a non-convex max-min optimization problem, subject to bounded CSI estimation errors, transmit power limits, and physical constraints on antenna displacement. By adopting an alternating optimization strategy, the original problem is decomposed into tractable subproblems, solved via techniques including the S-Procedure, Schur complement, and successive convex approximation. Numerical evaluations confirm that the proposed approach achieves substantial gains over existing benchmarks in terms of worst-case throughput.

Temporal Visual Semantics-Induced Human Motion Understanding with Large Language Models

Unsupervised human motion segmentation (HMS) can be effectively achieved using subspace clustering techniques. However, traditional methods overlook the role of temporal semantic exploration in HMS. This paper explores the use of temporal vision semantics (TVS) derived from human motion sequences, leveraging the image-to-text capabilities of a large language model (LLM) to enhance subspace clustering performance. The core idea is to extract textual motion information from consecutive frames via LLM and incorporate this learned information into the subspace clustering framework. The primary challenge lies in learning TVS from human motion sequences using LLM and integrating this information into subspace clustering. To address this, we determine whether consecutive frames depict the same motion by querying the LLM and subsequently learn temporal neighboring information based on its response. We then develop a TVS-integrated subspace clustering approach, incorporating subspace embedding with a temporal regularizer that induces each frame to share similar subspace embeddings with its temporal neighbors. Additionally, segmentation is performed based on subspace embedding with a temporal constraint that induces the grouping of each frame with its temporal neighbors. We also introduce a feedback-enabled framework that continuously optimizes subspace embedding based on the segmentation output. Experimental results demonstrate that the proposed method outperforms existing state-of-the-art approaches on four benchmark human motion datasets.

Unsupervised Radio Map Construction in Mixed LoS/NLoS Indoor Environments

Radio maps are essential for enhancing wireless communications and localization. However, existing methods for constructing radio maps typically require costly calibration pro- cesses to collect location-labeled channel state information (CSI) datasets. This paper aims to recover the data collection trajectory directly from the channel propagation sequence, eliminating the need for location calibration. The key idea is to employ a hidden Markov model (HMM)-based framework to conditionally model the channel propagation matrix, while simultaneously modeling the location correlation in the trajectory. The primary challenges involve modeling the complex relationship between channel propagation in multiple-input multiple-output (MIMO) networks and geographical locations, and addressing both line-of-sight (LOS) and non-line-of-sight (NLOS) indoor conditions. In this paper, we propose an HMM-based framework that jointly characterizes the conditional propagation model and the evolution of the user trajectory. Specifically, the channel propagation in MIMO networks is modeled separately in terms of power, delay, and angle, with distinct models for LOS and NLOS conditions. The user trajectory is modeled using a Gaussian-Markov model. The parameters for channel propagation, the mobility model, and LOS/NLOS classification are optimized simultaneously. Experimental validation using simulated MIMO-Orthogonal Frequency-Division Multiplexing (OFDM) networks with a multi-antenna uniform linear arrays (ULA) configuration demonstrates that the proposed method achieves an average localization accuracy of 0.65 meters in an indoor environment, covering both LOS and NLOS regions. Moreover, the constructed radio map enables localization with a reduced error compared to conventional supervised methods, such as k-nearest neighbors (KNN), support vector machine (SVM), and deep neural network (DNN).

Blind Construction of Angular Power Maps in Massive MIMO Networks

Channel state information (CSI) acquisition is a challenging problem in massive multiple-input multiple-output (MIMO) networks. Radio maps provide a promising solution for radio resource management by reducing online CSI acquisition. However, conventional approaches for radio map construction require location-labeled CSI data, which is challenging in practice. This paper investigates unsupervised angular power map construction based on large timescale CSI data collected in a massive MIMO network without location labels. A hidden Markov model (HMM) is built to connect the hidden trajectory of a mobile with the CSI evolution of a massive MIMO channel. As a result, the mobile location can be estimated, enabling the construction of an angular power map. We show that under uniform rectilinear mobility with Poisson-distributed base stations (BSs), the Cramer-Rao Lower Bound (CRLB) for localization error can vanish at any signal-to-noise ratios (SNRs), whereas when BSs are confined to a limited region, the error remains nonzero even with infinite independent measurements. Based on reference signal received power (RSRP) data collected in a real multi-cell massive MIMO network, an average localization error of 18 meters can be achieved although measurements are mainly obtained from a single serving cell.

Block-Diagonal Guided DBSCAN Clustering

Cluster analysis plays a crucial role in database mining, and one of the most widely used algorithms in this field is DBSCAN. However, DBSCAN has several limitations, such as difficulty in handling high-dimensional large-scale data, sensitivity to input parameters, and lack of robustness in producing clustering results. This paper introduces an improved version of DBSCAN that leverages the block-diagonal property of the similarity graph to guide the clustering procedure of DBSCAN. The key idea is to construct a graph that measures the similarity between high-dimensional large-scale data points and has the potential to be transformed into a block-diagonal form through an unknown permutation, followed by a cluster-ordering procedure to generate the desired permutation. The clustering structure can be easily determined by identifying the diagonal blocks in the permuted graph. We propose a gradient descent-based method to solve the proposed problem. Additionally, we develop a DBSCAN-based points traversal algorithm that identifies clusters with high densities in the graph and generates an augmented ordering of clusters. The block-diagonal structure of the graph is then achieved through permutation based on the traversal order, providing a flexible foundation for both automatic and interactive cluster analysis. We introduce a split-and-refine algorithm to automatically search for all diagonal blocks in the permuted graph with theoretically optimal guarantees under specific cases. We extensively evaluate our proposed approach on twelve challenging real-world benchmark clustering datasets and demonstrate its superior performance compared to the state-of-the-art clustering method on every dataset.

Constructing Indoor Region-based Radio Map without Location Labels

Radio map construction requires a large amount of radio measurement data with location labels, which imposes a high deployment cost. This paper develops a region-based radio map from received signal strength (RSS) measurements without location labels. The construction is based on a set of blindly collected RSS measurement data from a device that visits each region in an indoor area exactly once, where the footprints and timestamps are not recorded. The main challenge is to cluster the RSS data and match clusters with the physical regions. Classical clustering algorithms fail to work as the RSS data naturally appears as non-clustered due to multipaths and noise. In this paper, a signal subspace model with a sequential prior is constructed for the RSS data, and an integrated segmentation and clustering algorithm is developed, which is shown to find the globally optimal solution in a special case. Furthermore, the clustered data is matched with the physical regions using a graph-based approach. Based on real measurements from an office space, the proposed scheme reduces the region localization error by roughly 50% compared to a weighted centroid localization (WCL) baseline, and it even outperforms some supervised localization schemes, including k-nearest neighbor (KNN), support vector machine (SVM), and deep neural network (DNN), which require labeled data for training.

GAR: Generalized Autoregression for Multi-Fidelity Fusion

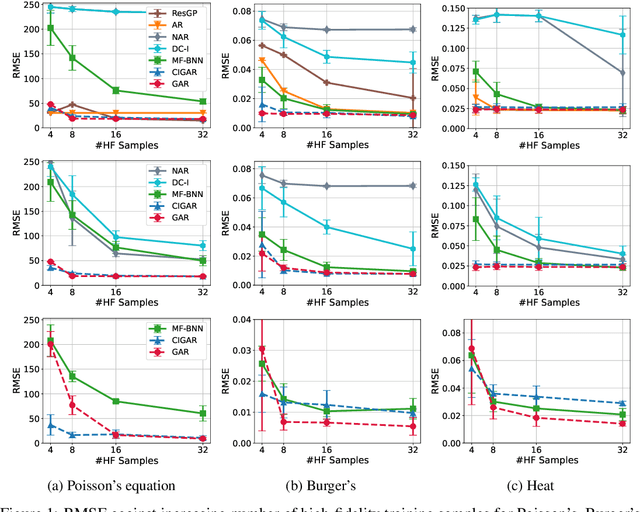
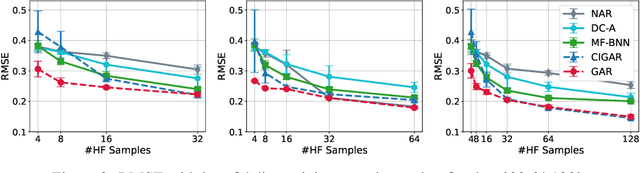
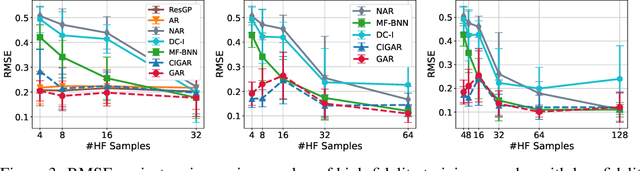
In many scientific research and engineering applications where repeated simulations of complex systems are conducted, a surrogate is commonly adopted to quickly estimate the whole system. To reduce the expensive cost of generating training examples, it has become a promising approach to combine the results of low-fidelity (fast but inaccurate) and high-fidelity (slow but accurate) simulations. Despite the fast developments of multi-fidelity fusion techniques, most existing methods require particular data structures and do not scale well to high-dimensional output. To resolve these issues, we generalize the classic autoregression (AR), which is wildly used due to its simplicity, robustness, accuracy, and tractability, and propose generalized autoregression (GAR) using tensor formulation and latent features. GAR can deal with arbitrary dimensional outputs and arbitrary multifidelity data structure to satisfy the demand of multi-fidelity fusion for complex problems; it admits a fully tractable likelihood and posterior requiring no approximate inference and scales well to high-dimensional problems. Furthermore, we prove the autokrigeability theorem based on GAR in the multi-fidelity case and develop CIGAR, a simplified GAR with the exact predictive mean accuracy with computation reduction by a factor of d 3, where d is the dimensionality of the output. The empirical assessment includes many canonical PDEs and real scientific examples and demonstrates that the proposed method consistently outperforms the SOTA methods with a large margin (up to 6x improvement in RMSE) with only a couple high-fidelity training samples.