Environment-Conditioned Diffusion Meta-Learning for Data-Efficient WiFi Localization

Fingerprinting-based localization often suffers from poor cross-environment generalization, especially when only a few labeled samples are available in the target environment. Existing methods mitigate distribution shifts through domain adaptation or improved signal representations, but they usually ignore environmental geometry or use it in a deterministic manner, limiting their ability to capture diverse multipath variations in complex propagation conditions. To address this issue, we propose EnvCoLoc, an environment-conditioned diffusion meta-learning framework for few-shot fingerprinting localization. EnvCoLoc extracts structured descriptors from 3D point clouds and uses them to condition a latent diffusion generator, which produces environment-specific parameter offsets to modulate a shared meta-learned initialization. This design injects geometry-aware priors into the adaptation process and provides more informative initializations for new environments. To learn the stochastic mapping from coarse environmental descriptors to high-dimensional parameter corrections under limited data, the diffusion generator and localization network are jointly optimized within a two-loop meta-learning framework. The generated offsets capture systematic environment-dependent variations, while gradient-based inner-loop adaptation further refines the model to reduce residual task-specific mismatch. We also provide an excess-loss analysis for finite-step adaptation, theoretically supporting the benefit of geometry-aware initialization. Real-world experiments show that EnvCoLoc consistently improves localization accuracy over baseline methods, achieving up to a 20.0% reduction in mean localization error in NLOS scenarios with only 10 support samples.

Temporal Visual Semantics-Induced Human Motion Understanding with Large Language Models

Unsupervised human motion segmentation (HMS) can be effectively achieved using subspace clustering techniques. However, traditional methods overlook the role of temporal semantic exploration in HMS. This paper explores the use of temporal vision semantics (TVS) derived from human motion sequences, leveraging the image-to-text capabilities of a large language model (LLM) to enhance subspace clustering performance. The core idea is to extract textual motion information from consecutive frames via LLM and incorporate this learned information into the subspace clustering framework. The primary challenge lies in learning TVS from human motion sequences using LLM and integrating this information into subspace clustering. To address this, we determine whether consecutive frames depict the same motion by querying the LLM and subsequently learn temporal neighboring information based on its response. We then develop a TVS-integrated subspace clustering approach, incorporating subspace embedding with a temporal regularizer that induces each frame to share similar subspace embeddings with its temporal neighbors. Additionally, segmentation is performed based on subspace embedding with a temporal constraint that induces the grouping of each frame with its temporal neighbors. We also introduce a feedback-enabled framework that continuously optimizes subspace embedding based on the segmentation output. Experimental results demonstrate that the proposed method outperforms existing state-of-the-art approaches on four benchmark human motion datasets.

Block-Diagonal Guided DBSCAN Clustering

Cluster analysis plays a crucial role in database mining, and one of the most widely used algorithms in this field is DBSCAN. However, DBSCAN has several limitations, such as difficulty in handling high-dimensional large-scale data, sensitivity to input parameters, and lack of robustness in producing clustering results. This paper introduces an improved version of DBSCAN that leverages the block-diagonal property of the similarity graph to guide the clustering procedure of DBSCAN. The key idea is to construct a graph that measures the similarity between high-dimensional large-scale data points and has the potential to be transformed into a block-diagonal form through an unknown permutation, followed by a cluster-ordering procedure to generate the desired permutation. The clustering structure can be easily determined by identifying the diagonal blocks in the permuted graph. We propose a gradient descent-based method to solve the proposed problem. Additionally, we develop a DBSCAN-based points traversal algorithm that identifies clusters with high densities in the graph and generates an augmented ordering of clusters. The block-diagonal structure of the graph is then achieved through permutation based on the traversal order, providing a flexible foundation for both automatic and interactive cluster analysis. We introduce a split-and-refine algorithm to automatically search for all diagonal blocks in the permuted graph with theoretically optimal guarantees under specific cases. We extensively evaluate our proposed approach on twelve challenging real-world benchmark clustering datasets and demonstrate its superior performance compared to the state-of-the-art clustering method on every dataset.

Box-Aware Feature Enhancement for Single Object Tracking on Point Clouds

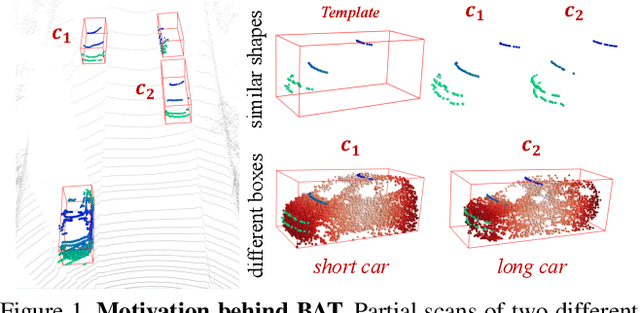
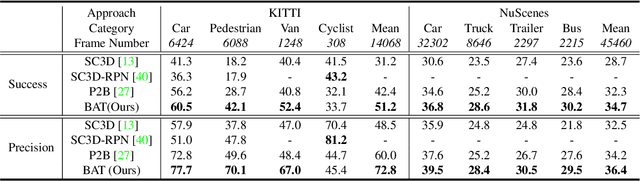
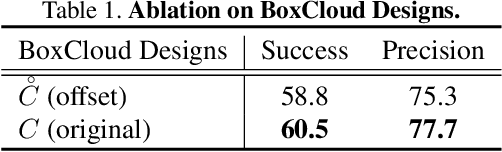
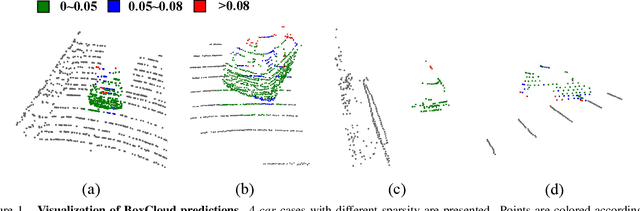
Current 3D single object tracking approaches track the target based on a feature comparison between the target template and the search area. However, due to the common occlusion in LiDAR scans, it is non-trivial to conduct accurate feature comparisons on severe sparse and incomplete shapes. In this work, we exploit the ground truth bounding box given in the first frame as a strong cue to enhance the feature description of the target object, enabling a more accurate feature comparison in a simple yet effective way. In particular, we first propose the BoxCloud, an informative and robust representation, to depict an object using the point-to-box relation. We further design an efficient box-aware feature fusion module, which leverages the aforementioned BoxCloud for reliable feature matching and embedding. Integrating the proposed general components into an existing model P2B, we construct a superior box-aware tracker (BAT). Experiments confirm that our proposed BAT outperforms the previous state-of-the-art by a large margin on both KITTI and NuScenes benchmarks, achieving a 12.8% improvement in terms of precision while running ~20% faster.

PointLIE: Locally Invertible Embedding for Point Cloud Sampling and Recovery

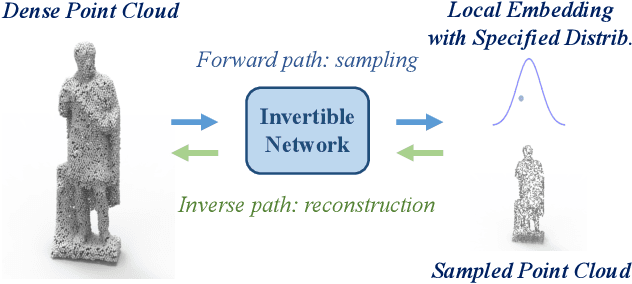
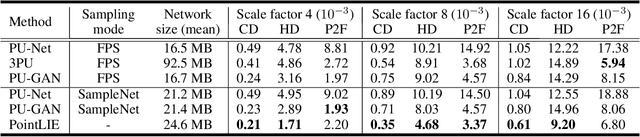
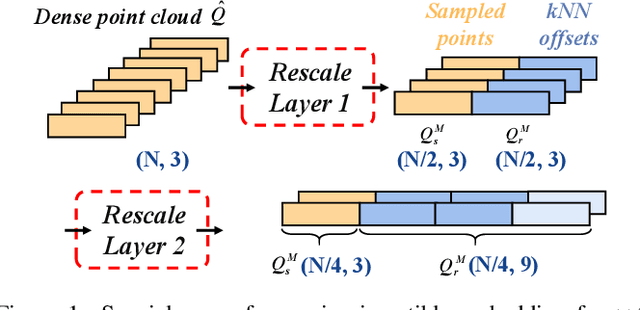
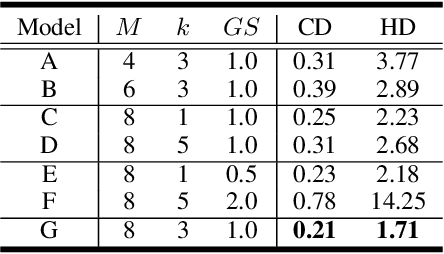
Point Cloud Sampling and Recovery (PCSR) is critical for massive real-time point cloud collection and processing since raw data usually requires large storage and computation. In this paper, we address a fundamental problem in PCSR: How to downsample the dense point cloud with arbitrary scales while preserving the local topology of discarding points in a case-agnostic manner (i.e. without additional storage for point relationship)? We propose a novel Locally Invertible Embedding for point cloud adaptive sampling and recovery (PointLIE). Instead of learning to predict the underlying geometry details in a seemingly plausible manner, PointLIE unifies point cloud sampling and upsampling to one single framework through bi-directional learning. Specifically, PointLIE recursively samples and adjusts neighboring points on each scale. Then it encodes the neighboring offsets of sampled points to a latent space and thus decouples the sampled points and the corresponding local geometric relationship. Once the latent space is determined and that the deep model is optimized, the recovery process could be conducted by passing the recover-pleasing sampled points and a randomly-drawn embedding to the same network through an invertible operation. Such a scheme could guarantee the fidelity of dense point recovery from sampled points. Extensive experiments demonstrate that the proposed PointLIE outperforms state-of-the-arts both quantitatively and qualitatively. Our code is released through https://github.com/zwb0/PointLIE.