CircuitVAE: Efficient and Scalable Latent Circuit Optimization

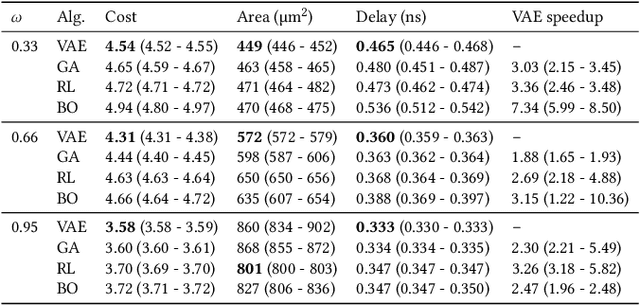
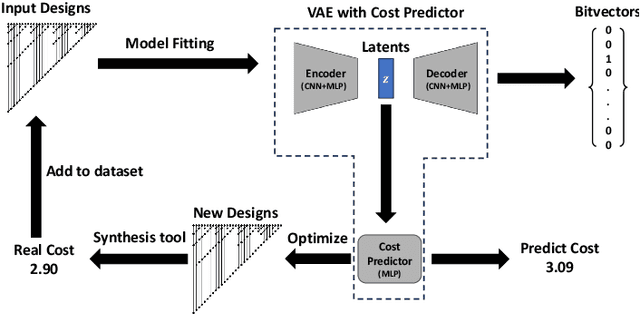
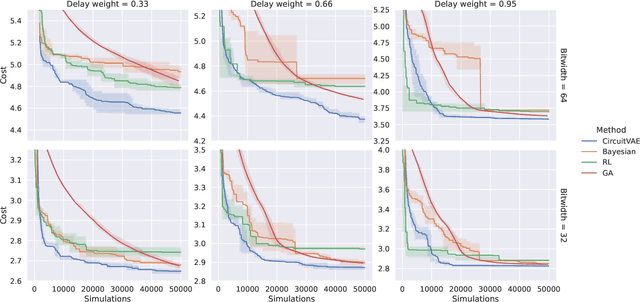
Automatically designing fast and space-efficient digital circuits is challenging because circuits are discrete, must exactly implement the desired logic, and are costly to simulate. We address these challenges with CircuitVAE, a search algorithm that embeds computation graphs in a continuous space and optimizes a learned surrogate of physical simulation by gradient descent. By carefully controlling overfitting of the simulation surrogate and ensuring diverse exploration, our algorithm is highly sample-efficient, yet gracefully scales to large problem instances and high sample budgets. We test CircuitVAE by designing binary adders across a large range of sizes, IO timing constraints, and sample budgets. Our method excels at designing large circuits, where other algorithms struggle: compared to reinforcement learning and genetic algorithms, CircuitVAE typically finds 64-bit adders which are smaller and faster using less than half the sample budget. We also find CircuitVAE can design state-of-the-art adders in a real-world chip, demonstrating that our method can outperform commercial tools in a realistic setting.

ChipNeMo: Domain-Adapted LLMs for Chip Design

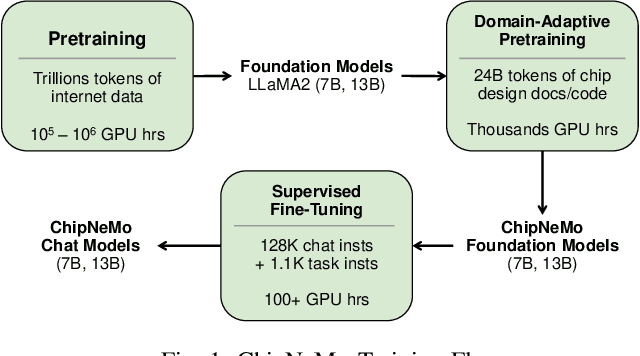
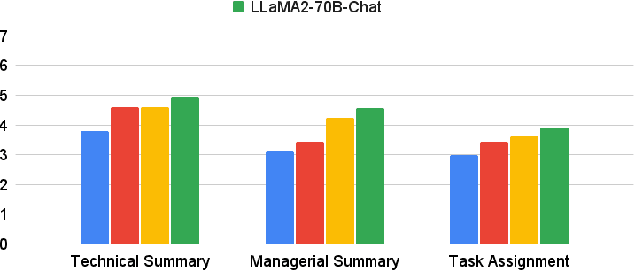
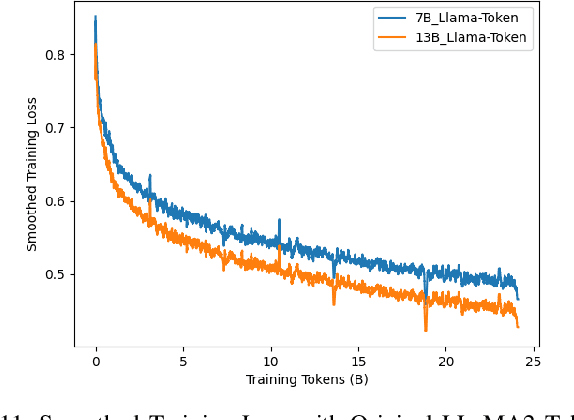
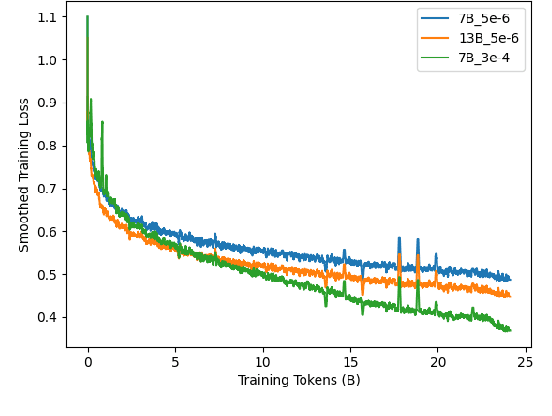
ChipNeMo aims to explore the applications of large language models (LLMs) for industrial chip design. Instead of directly deploying off-the-shelf commercial or open-source LLMs, we instead adopt the following domain adaptation techniques: custom tokenizers, domain-adaptive continued pretraining, supervised fine-tuning (SFT) with domain-specific instructions, and domain-adapted retrieval models. We evaluate these methods on three selected LLM applications for chip design: an engineering assistant chatbot, EDA script generation, and bug summarization and analysis. Our results show that these domain adaptation techniques enable significant LLM performance improvements over general-purpose base models across the three evaluated applications, enabling up to 5x model size reduction with similar or better performance on a range of design tasks. Our findings also indicate that there's still room for improvement between our current results and ideal outcomes. We believe that further investigation of domain-adapted LLM approaches will help close this gap in the future.

Solving High Frequency and Multi-Scale PDEs with Gaussian Processes

Machine learning based solvers have garnered much attention in physical simulation and scientific computing, with a prominent example, physics-informed neural networks (PINNs). However, PINNs often struggle to solve high-frequency and multi-scale PDEs, which can be due to spectral bias during neural network training. To address this problem, we resort to the Gaussian process (GP) framework. To flexibly capture the dominant frequencies, we model the power spectrum of the PDE solution with a student t mixture or Gaussian mixture. We then apply the inverse Fourier transform to obtain the covariance function (according to the Wiener-Khinchin theorem). The covariance derived from the Gaussian mixture spectrum corresponds to the known spectral mixture kernel. We are the first to discover its rationale and effectiveness for PDE solving. Next,we estimate the mixture weights in the log domain, which we show is equivalent to placing a Jeffreys prior. It automatically induces sparsity, prunes excessive frequencies, and adjusts the remaining toward the ground truth. Third, to enable efficient and scalable computation on massive collocation points, which are critical to capture high frequencies, we place the collocation points on a grid, and multiply our covariance function at each input dimension. We use the GP conditional mean to predict the solution and its derivatives so as to fit the boundary condition and the equation itself. As a result, we can derive a Kronecker product structure in the covariance matrix. We use Kronecker product properties and multilinear algebra to greatly promote computational efficiency and scalability, without any low-rank approximations. We show the advantage of our method in systematic experiments.

Streaming Factor Trajectory Learning for Temporal Tensor Decomposition

Practical tensor data is often along with time information. Most existing temporal decomposition approaches estimate a set of fixed factors for the objects in each tensor mode, and hence cannot capture the temporal evolution of the objects' representation. More important, we lack an effective approach to capture such evolution from streaming data, which is common in real-world applications. To address these issues, we propose Streaming Factor Trajectory Learning for temporal tensor decomposition. We use Gaussian processes (GPs) to model the trajectory of factors so as to flexibly estimate their temporal evolution. To address the computational challenges in handling streaming data, we convert the GPs into a state-space prior by constructing an equivalent stochastic differential equation (SDE). We develop an efficient online filtering algorithm to estimate a decoupled running posterior of the involved factor states upon receiving new data. The decoupled estimation enables us to conduct standard Rauch-Tung-Striebel smoothing to compute the full posterior of all the trajectories in parallel, without the need for revisiting any previous data. We have shown the advantage of SFTL in both synthetic tasks and real-world applications. The code is available at {https://github.com/xuangu-fang/Streaming-Factor-Trajectory-Learning}.

Genetic Programming Based Symbolic Regression for Analytical Solutions to Differential Equations

In this paper, we present a machine learning method for the discovery of analytic solutions to differential equations. The method utilizes an inherently interpretable algorithm, genetic programming based symbolic regression. Unlike conventional accuracy measures in machine learning we demonstrate the ability to recover true analytic solutions, as opposed to a numerical approximation. The method is verified by assessing its ability to recover known analytic solutions for two separate differential equations. The developed method is compared to a conventional, purely data-driven genetic programming based symbolic regression algorithm. The reliability of successful evolution of the true solution, or an algebraic equivalent, is demonstrated.

PrefixRL: Optimization of Parallel Prefix Circuits using Deep Reinforcement Learning

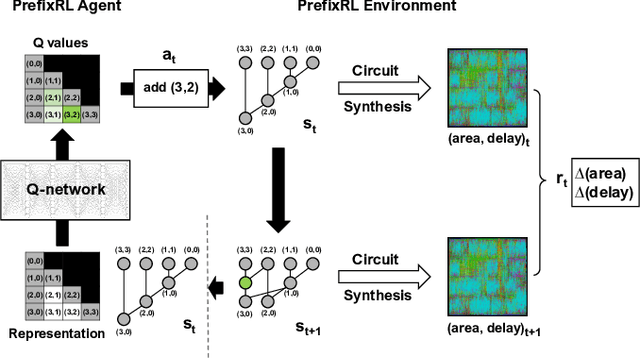
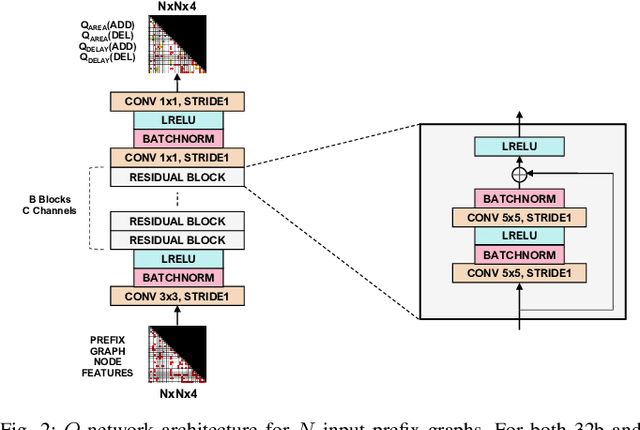
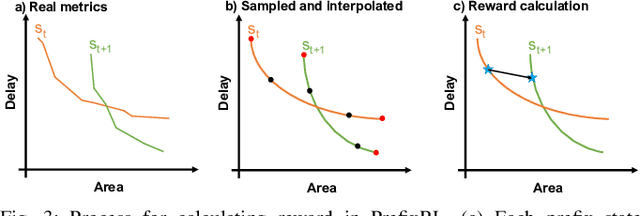
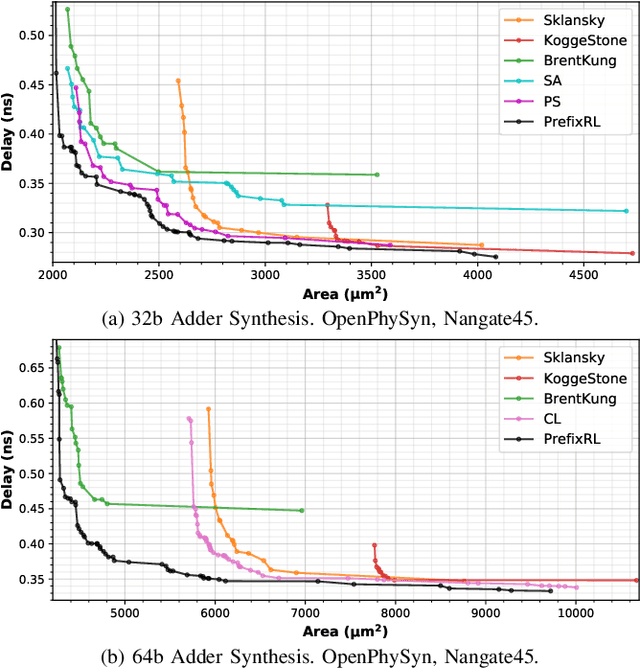
In this work, we present a reinforcement learning (RL) based approach to designing parallel prefix circuits such as adders or priority encoders that are fundamental to high-performance digital design. Unlike prior methods, our approach designs solutions tabula rasa purely through learning with synthesis in the loop. We design a grid-based state-action representation and an RL environment for constructing legal prefix circuits. Deep Convolutional RL agents trained on this environment produce prefix adder circuits that Pareto-dominate existing baselines with up to 16.0% and 30.2% lower area for the same delay in the 32b and 64b settings respectively. We observe that agents trained with open-source synthesis tools and cell library can design adder circuits that achieve lower area and delay than commercial tool adders in an industrial cell library.

AutoIP: A United Framework to Integrate Physics into Gaussian Processes

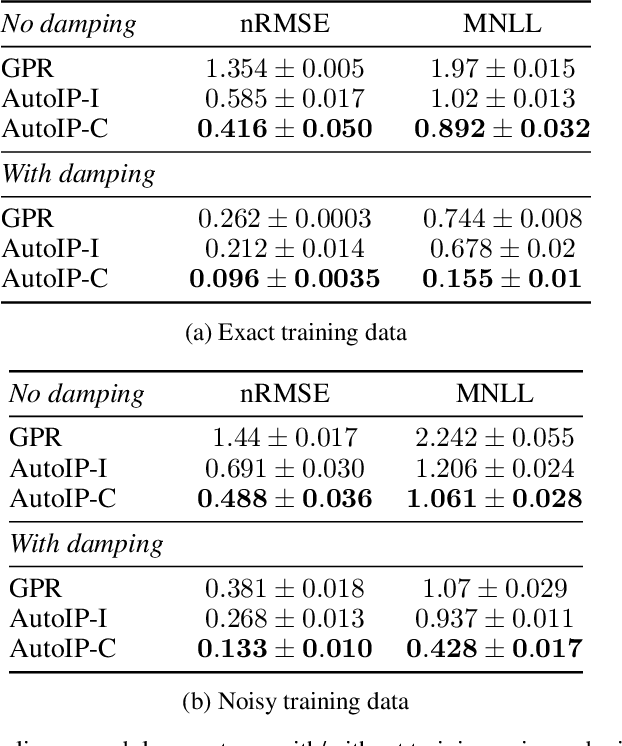
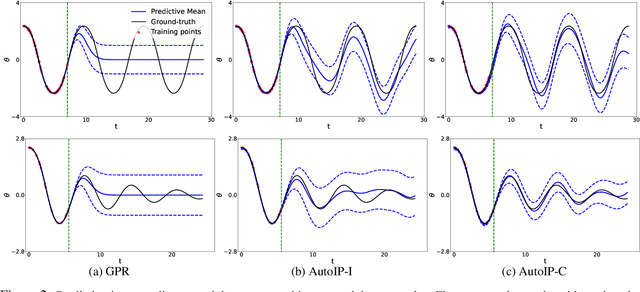
Physics modeling is critical for modern science and engineering applications. From data science perspective, physics knowledge -- often expressed as differential equations -- is valuable in that it is highly complementary to data, and can potentially help overcome data sparsity, noise, inaccuracy, etc. In this work, we propose a simple yet powerful framework that can integrate all kinds of differential equations into Gaussian processes (GPs) to enhance prediction accuracy and uncertainty quantification. These equations can be linear, nonlinear, temporal, time-spatial, complete, incomplete with unknown source terms, etc. Specifically, based on kernel differentiation, we construct a GP prior to jointly sample the values of the target function, equation-related derivatives, and latent source functions from a multivariate Gaussian distribution. The sampled values are fed to two likelihoods -- one is to fit the observations and the other to conform to the equation. We use the whitening trick to evade the strong dependency between the sampled function values and kernel parameters, and develop a stochastic variational learning algorithm. Our method shows improvement upon vanilla GPs in both simulation and several real-world applications, even using rough, incomplete equations.

Meta-Learning with Adjoint Methods

Model Agnostic Meta-Learning (MAML) is widely used to find a good initialization for a family of tasks. Despite its success, a critical challenge in MAML is to calculate the gradient w.r.t the initialization of a long training trajectory for the sampled tasks, because the computation graph can rapidly explode and the computational cost is very expensive. To address this problem, we propose Adjoint MAML (A-MAML). We view gradient descent in the inner optimization as the evolution of an Ordinary Differential Equation (ODE). To efficiently compute the gradient of the validation loss w.r.t the initialization, we use the adjoint method to construct a companion, backward ODE. To obtain the gradient w.r.t the initialization, we only need to run the standard ODE solver twice -- one is forward in time that evolves a long trajectory of gradient flow for the sampled task; the other is backward and solves the adjoint ODE. We need not create or expand any intermediate computational graphs, adopt aggressive approximations, or impose proximal regularizers in the training loss. Our approach is cheap, accurate, and adaptable to different trajectory lengths. We demonstrate the advantage of our approach in both synthetic and real-world meta-learning tasks.

Guiding Global Placement With Reinforcement Learning

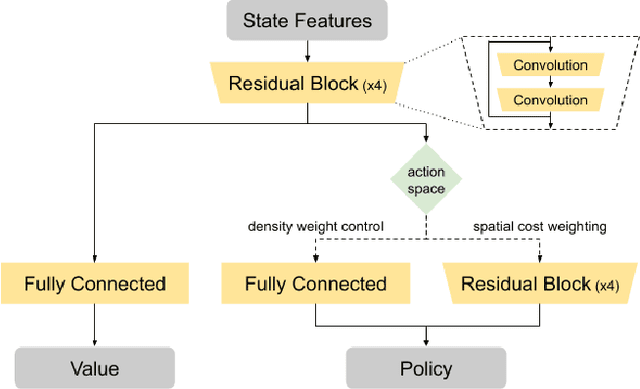
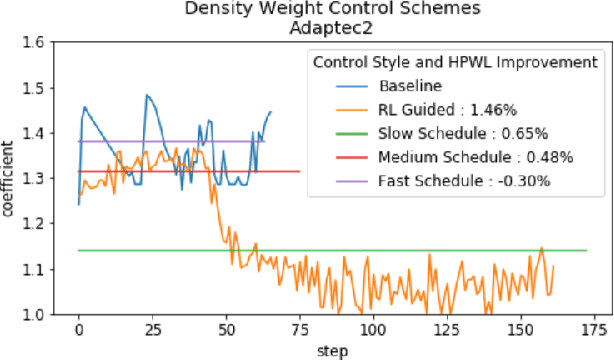
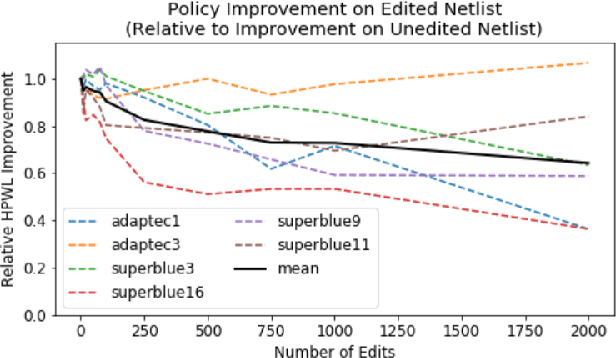
Recent advances in GPU accelerated global and detail placement have reduced the time to solution by an order of magnitude. This advancement allows us to leverage data driven optimization (such as Reinforcement Learning) in an effort to improve the final quality of placement results. In this work we augment state-of-the-art, force-based global placement solvers with a reinforcement learning agent trained to improve the final detail placed Half Perimeter Wire Length (HPWL). We propose novel control schemes with either global or localized control of the placement process. We then train reinforcement learning agents to use these controls to guide placement to improved solutions. In both cases, the augmented optimizer finds improved placement solutions. Our trained agents achieve an average 1% improvement in final detail place HPWL across a range of academic benchmarks and more than 1% in global place HPWL on real industry designs.

Physics Regularized Gaussian Processes

We consider incorporating incomplete physics knowledge, expressed as differential equations with latent functions, into Gaussian processes (GPs) to improve their performance, especially for limited data and extrapolation. While existing works have successfully encoded such knowledge via kernel convolution, they only apply to linear equations with analytical Green's functions. The convolution can further restrict us from fusing physics with highly expressive kernels, e.g., deep kernels. To overcome these limitations, we propose Physics Regularized Gaussian Process (PRGP) that can incorporate both linear and nonlinear equations, does not rely on Green's functions, and is free to use arbitrary kernels. Specifically, we integrate the standard GP with a generative model to encode the differential equation in a principled Bayesian hybrid framework. For efficient and effective inference, we marginalize out the latent variables and derive a simplified model evidence lower bound (ELBO), based on which we develop a stochastic collapsed inference algorithm. Our ELBO can be viewed as a posterior regularization objective. We show the advantage of our approach in both simulation and real-world applications.