Towards Foundation Models for Scientific Machine Learning: Characterizing Scaling and Transfer Behavior

Pre-trained machine learning (ML) models have shown great performance for a wide range of applications, in particular in natural language processing (NLP) and computer vision (CV). Here, we study how pre-training could be used for scientific machine learning (SciML) applications, specifically in the context of transfer learning. We study the transfer behavior of these models as (i) the pre-trained model size is scaled, (ii) the downstream training dataset size is scaled, (iii) the physics parameters are systematically pushed out of distribution, and (iv) how a single model pre-trained on a mixture of different physics problems can be adapted to various downstream applications. We find that-when fine-tuned appropriately-transfer learning can help reach desired accuracy levels with orders of magnitude fewer downstream examples (across different tasks that can even be out-of-distribution) than training from scratch, with consistent behavior across a wide range of downstream examples. We also find that fine-tuning these models yields more performance gains as model size increases, compared to training from scratch on new downstream tasks. These results hold for a broad range of PDE learning tasks. All in all, our results demonstrate the potential of the "pre-train and fine-tune" paradigm for SciML problems, demonstrating a path towards building SciML foundation models. We open-source our code for reproducibility.

GACT: Activation Compressed Training for General Architectures

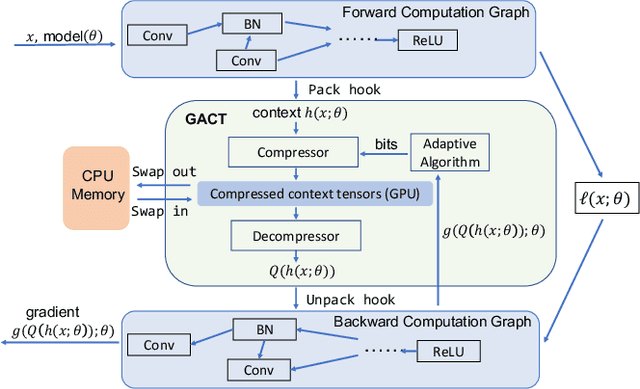
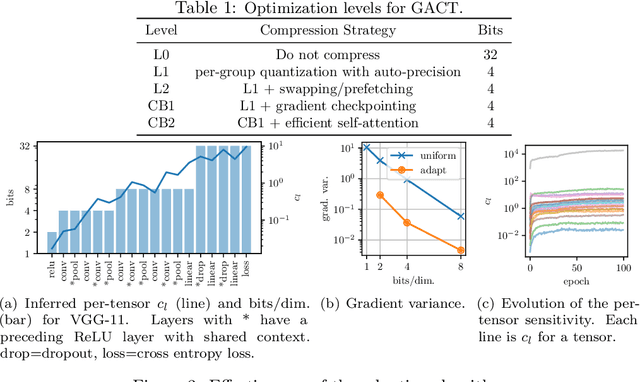
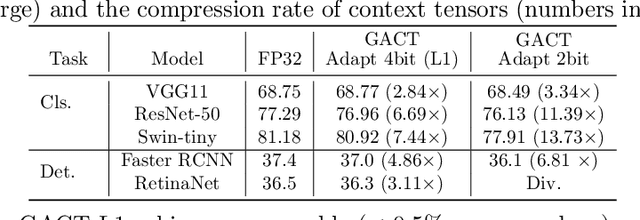
Training large neural network (NN) models requires extensive memory resources, and Activation Compressed Training (ACT) is a promising approach to reduce training memory footprint. This paper presents GACT, an ACT framework to support a broad range of machine learning tasks for generic NN architectures with limited domain knowledge. By analyzing a linearized version of ACT's approximate gradient, we prove the convergence of GACT without prior knowledge on operator type or model architecture. To make training stable, we propose an algorithm that decides the compression ratio for each tensor by estimating its impact on the gradient at run time. We implement GACT as a PyTorch library that readily applies to any NN architecture. GACT reduces the activation memory for convolutional NNs, transformers, and graph NNs by up to 8.1x, enabling training with a 4.2x to 24.7x larger batch size, with negligible accuracy loss.

AutoIP: A United Framework to Integrate Physics into Gaussian Processes

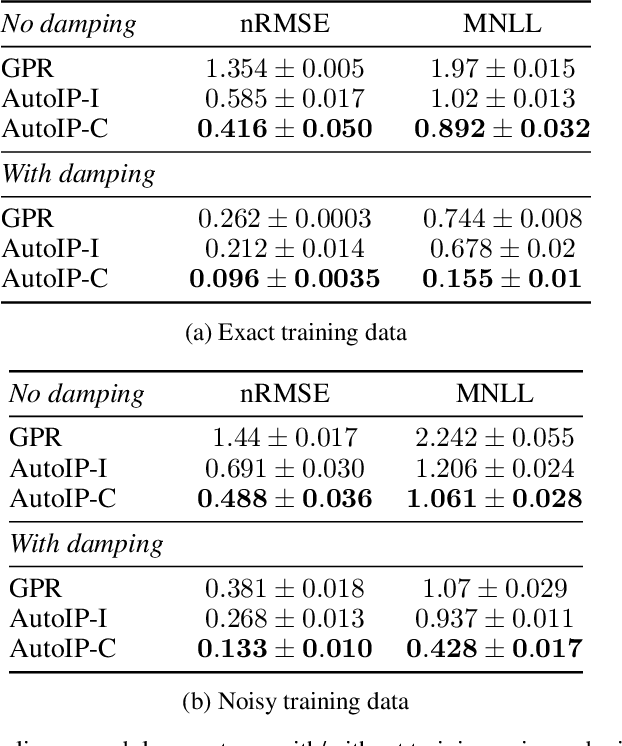
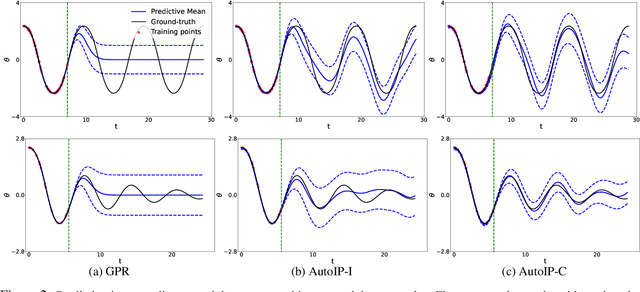
Physics modeling is critical for modern science and engineering applications. From data science perspective, physics knowledge -- often expressed as differential equations -- is valuable in that it is highly complementary to data, and can potentially help overcome data sparsity, noise, inaccuracy, etc. In this work, we propose a simple yet powerful framework that can integrate all kinds of differential equations into Gaussian processes (GPs) to enhance prediction accuracy and uncertainty quantification. These equations can be linear, nonlinear, temporal, time-spatial, complete, incomplete with unknown source terms, etc. Specifically, based on kernel differentiation, we construct a GP prior to jointly sample the values of the target function, equation-related derivatives, and latent source functions from a multivariate Gaussian distribution. The sampled values are fed to two likelihoods -- one is to fit the observations and the other to conform to the equation. We use the whitening trick to evade the strong dependency between the sampled function values and kernel parameters, and develop a stochastic variational learning algorithm. Our method shows improvement upon vanilla GPs in both simulation and several real-world applications, even using rough, incomplete equations.

LocalNewton: Reducing Communication Bottleneck for Distributed Learning

To address the communication bottleneck problem in distributed optimization within a master-worker framework, we propose LocalNewton, a distributed second-order algorithm with local averaging. In LocalNewton, the worker machines update their model in every iteration by finding a suitable second-order descent direction using only the data and model stored in their own local memory. We let the workers run multiple such iterations locally and communicate the models to the master node only once every few (say L) iterations. LocalNewton is highly practical since it requires only one hyperparameter, the number L of local iterations. We use novel matrix concentration-based techniques to obtain theoretical guarantees for LocalNewton, and we validate them with detailed empirical evaluation. To enhance practicability, we devise an adaptive scheme to choose L, and we show that this reduces the number of local iterations in worker machines between two model synchronizations as the training proceeds, successively refining the model quality at the master. Via extensive experiments using several real-world datasets with AWS Lambda workers and an AWS EC2 master, we show that LocalNewton requires fewer than 60% of the communication rounds (between master and workers) and less than 40% of the end-to-end running time, compared to state-of-the-art algorithms, to reach the same training~loss.

Rethinking Batch Normalization in Transformers

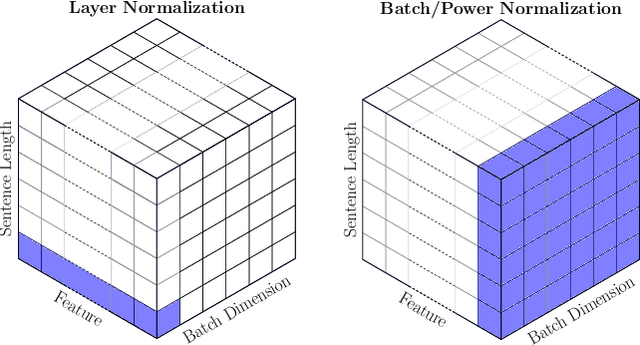
The standard normalization method for neural network (NN) models used in Natural Language Processing (NLP) is layer normalization (LN). This is different than batch normalization (BN), which is widely-adopted in Computer Vision. The preferred use of LN in NLP is principally due to the empirical observation that a (naive/vanilla) use of BN leads to significant performance degradation for NLP tasks; however, a thorough understanding of the underlying reasons for this is not always evident. In this paper, we perform a systematic study of NLP transformer models to understand why BN has a poor performance, as compared to LN. We find that the statistics of NLP data across the batch dimension exhibit large fluctuations throughout training. This results in instability, if BN is naively implemented. To address this, we propose Power Normalization (PN), a novel normalization scheme that resolves this issue by (i) relaxing zero-mean normalization in BN, (ii) incorporating a running quadratic mean instead of per batch statistics to stabilize fluctuations, and (iii) using an approximate backpropagation for incorporating the running statistics in the forward pass. We show theoretically, under mild assumptions, that PN leads to a smaller Lipschitz constant for the loss, compared with BN. Furthermore, we prove that the approximate backpropagation scheme leads to bounded gradients. We extensively test PN for transformers on a range of NLP tasks, and we show that it significantly outperforms both LN and BN. In particular, PN outperforms LN by 0.4/0.6 BLEU on IWSLT14/WMT14 and 5.6/3.0 PPL on PTB/WikiText-103.

PyHessian: Neural Networks Through the Lens of the Hessian

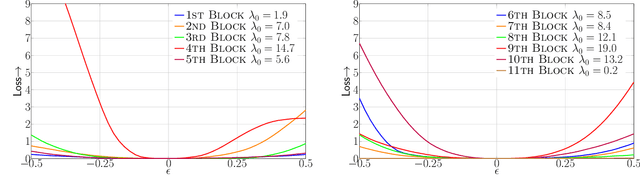
We present PyHessian, a new scalable framework that enables fast computation of Hessian (i.e., second-order derivative) information for deep neural networks. This framework is developed in Pytorch, and it enables distributed-memory execution on both cloud and supercomputer systems. PyHessian enables fast computations of the top Hessian eigenvalues, the Hessian trace, and the full Hessian eigenvalue/spectral density. This general framework can be used to analyze neural network models, including the topology of the loss landscape (i.e., curvature information) to gain insight into the behavior of different models/optimizers. To illustrate this, we apply PyHessian to analyze the effect of residual connections and Batch Normalization layers on the smoothness of the loss landscape during training. One recent claim, based on simpler first-order analysis, is that residual connections and Batch Normalization make the loss landscape ``smoother,'' thus making it easier for Stochastic Gradient Descent to converge to a good solution. We perform an extensive analysis of this hypothesis, on four residual networks (ResNet20/32/38/56) on the Cifar-10/100 dataset, by measuring directly the Hessian spectrum using PyHessian. This analysis leads to finer-scale insight, demonstrating that while conventional wisdom is sometimes validated, in other cases it is simply incorrect. In particular, we find that Batch Normalization layers do not necessarily make the loss landscape smoother, especially for shallow networks. Instead, the claimed smoother loss landscape only becomes evident for deeper neural networks, at least within this ResNet series. We have open-sourced the PyHessian framework for Hessian spectrum computation.

ANODEV2: A Coupled Neural ODE Evolution Framework

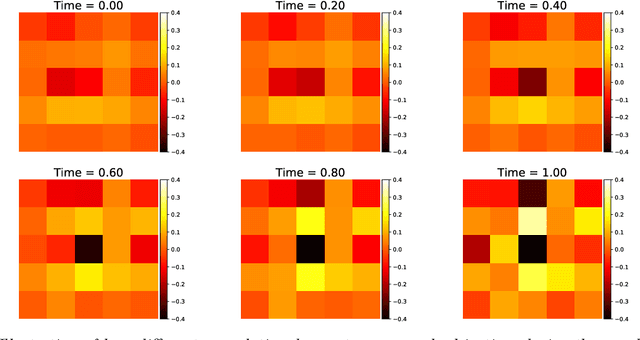
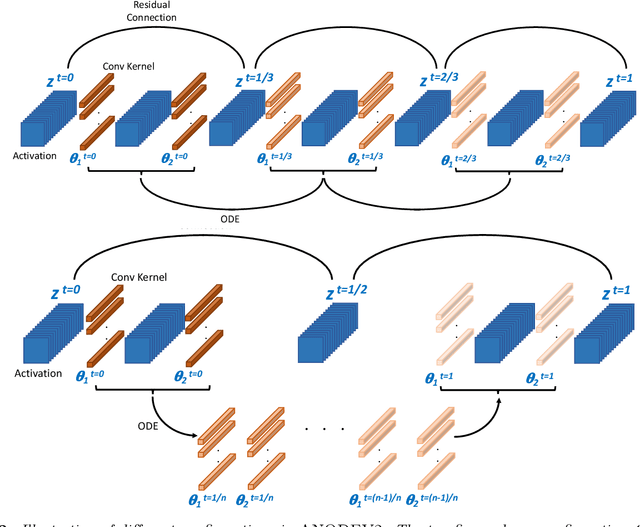
It has been observed that residual networks can be viewed as the explicit Euler discretization of an Ordinary Differential Equation (ODE). This observation motivated the introduction of so-called Neural ODEs, which allow more general discretization schemes with adaptive time stepping. Here, we propose ANODEV2, which is an extension of this approach that also allows evolution of the neural network parameters, in a coupled ODE-based formulation. The Neural ODE method introduced earlier is in fact a special case of this new more general framework. We present the formulation of ANODEV2, derive optimality conditions, and implement a coupled reaction-diffusion-advection version of this framework in PyTorch. We present empirical results using several different configurations of ANODEV2, testing them on multiple models on CIFAR-10. We report results showing that this coupled ODE-based framework is indeed trainable, and that it achieves higher accuracy, as compared to the baseline models as well as the recently-proposed Neural ODE approach.

HAWQ: Hessian AWare Quantization of Neural Networks with Mixed-Precision

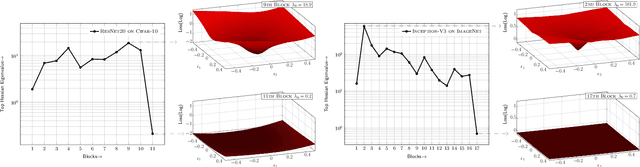
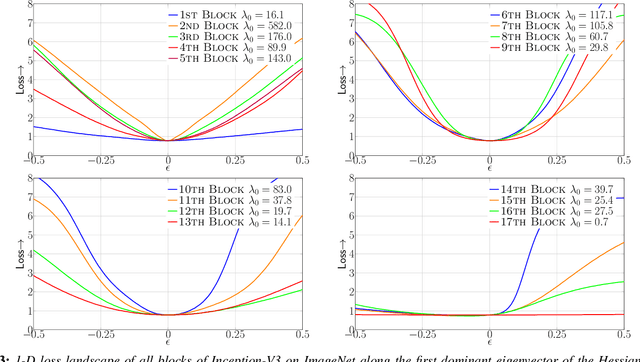
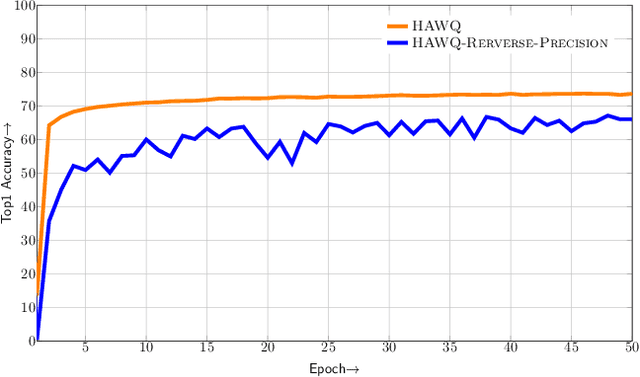
Model size and inference speed/power have become a major challenge in the deployment of Neural Networks for many applications. A promising approach to address these problems is quantization. However, uniformly quantizing a model to ultra low precision leads to significant accuracy degradation. A novel solution for this is to use mixed-precision quantization, as some parts of the network may allow lower precision as compared to other layers. However, there is no systematic way to determine the precision of different layers. A brute force approach is not feasible for deep networks, as the search space for mixed-precision is exponential in the number of layers. Another challenge is a similar factorial complexity for determining block-wise fine-tuning order when quantizing the model to a target precision. Here, we introduce Hessian AWare Quantization (HAWQ), a novel second-order quantization method to address these problems. HAWQ allows for the automatic selection of the relative quantization precision of each layer, based on the layer's Hessian spectrum. Moreover, HAWQ provides a deterministic fine-tuning order for quantizing layers, based on second-order information. We show the results of our method on Cifar-10 using ResNet20, and on ImageNet using Inception-V3, ResNet50 and SqueezeNext models. Comparing HAWQ with state-of-the-art shows that we can achieve similar/better accuracy with $8\times$ activation compression ratio on ResNet20, as compared to DNAS~\cite{wu2018mixed}, and up to $1\%$ higher accuracy with up to $14\%$ smaller models on ResNet50 and Inception-V3, compared to recently proposed methods of RVQuant~\cite{park2018value} and HAQ~\cite{wang2018haq}. Furthermore, we show that we can quantize SqueezeNext to just 1MB model size while achieving above $68\%$ top1 accuracy on ImageNet.