Towards Fast, Specialized Machine Learning Force Fields: Distilling Foundation Models via Energy Hessians

The foundation model (FM) paradigm is transforming Machine Learning Force Fields (MLFFs), leveraging general-purpose representations and scalable training to perform a variety of computational chemistry tasks. Although MLFF FMs have begun to close the accuracy gap relative to first-principles methods, there is still a strong need for faster inference speed. Additionally, while research is increasingly focused on general-purpose models which transfer across chemical space, practitioners typically only study a small subset of systems at a given time. This underscores the need for fast, specialized MLFFs relevant to specific downstream applications, which preserve test-time physical soundness while maintaining train-time scalability. In this work, we introduce a method for transferring general-purpose representations from MLFF foundation models to smaller, faster MLFFs specialized to specific regions of chemical space. We formulate our approach as a knowledge distillation procedure, where the smaller "student" MLFF is trained to match the Hessians of the energy predictions of the "teacher" foundation model. Our specialized MLFFs can be up to 20 $\times$ faster than the original foundation model, while retaining, and in some cases exceeding, its performance and that of undistilled models. We also show that distilling from a teacher model with a direct force parameterization into a student model trained with conservative forces (i.e., computed as derivatives of the potential energy) successfully leverages the representations from the large-scale teacher for improved accuracy, while maintaining energy conservation during test-time molecular dynamics simulations. More broadly, our work suggests a new paradigm for MLFF development, in which foundation models are released along with smaller, specialized simulation "engines" for common chemical subsets.

Scaling physics-informed hard constraints with mixture-of-experts

Imposing known physical constraints, such as conservation laws, during neural network training introduces an inductive bias that can improve accuracy, reliability, convergence, and data efficiency for modeling physical dynamics. While such constraints can be softly imposed via loss function penalties, recent advancements in differentiable physics and optimization improve performance by incorporating PDE-constrained optimization as individual layers in neural networks. This enables a stricter adherence to physical constraints. However, imposing hard constraints significantly increases computational and memory costs, especially for complex dynamical systems. This is because it requires solving an optimization problem over a large number of points in a mesh, representing spatial and temporal discretizations, which greatly increases the complexity of the constraint. To address this challenge, we develop a scalable approach to enforce hard physical constraints using Mixture-of-Experts (MoE), which can be used with any neural network architecture. Our approach imposes the constraint over smaller decomposed domains, each of which is solved by an "expert" through differentiable optimization. During training, each expert independently performs a localized backpropagation step by leveraging the implicit function theorem; the independence of each expert allows for parallelization across multiple GPUs. Compared to standard differentiable optimization, our scalable approach achieves greater accuracy in the neural PDE solver setting for predicting the dynamics of challenging non-linear systems. We also improve training stability and require significantly less computation time during both training and inference stages.

Neural Spectral Methods: Self-supervised learning in the spectral domain

We present Neural Spectral Methods, a technique to solve parametric Partial Differential Equations (PDEs), grounded in classical spectral methods. Our method uses orthogonal bases to learn PDE solutions as mappings between spectral coefficients. In contrast to current machine learning approaches which enforce PDE constraints by minimizing the numerical quadrature of the residuals in the spatiotemporal domain, we leverage Parseval's identity and introduce a new training strategy through a \textit{spectral loss}. Our spectral loss enables more efficient differentiation through the neural network, and substantially reduces training complexity. At inference time, the computational cost of our method remains constant, regardless of the spatiotemporal resolution of the domain. Our experimental results demonstrate that our method significantly outperforms previous machine learning approaches in terms of speed and accuracy by one to two orders of magnitude on multiple different problems. When compared to numerical solvers of the same accuracy, our method demonstrates a $10\times$ increase in performance speed.

AutoIP: A United Framework to Integrate Physics into Gaussian Processes

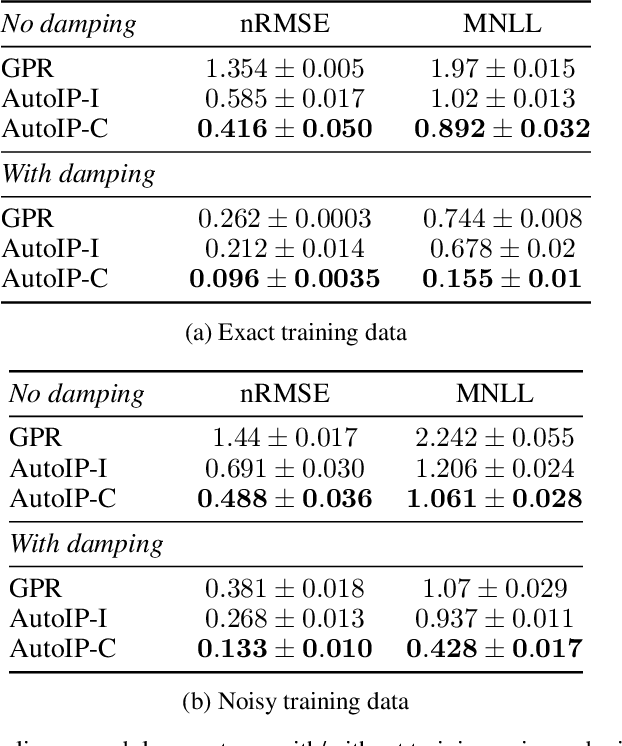
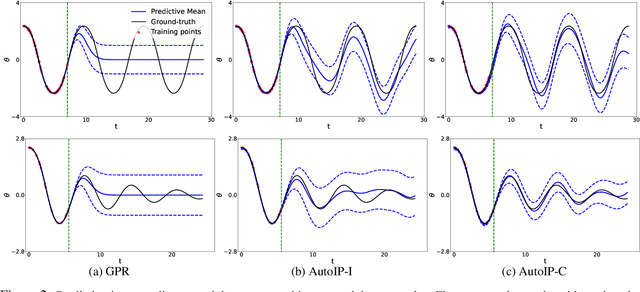
Physics modeling is critical for modern science and engineering applications. From data science perspective, physics knowledge -- often expressed as differential equations -- is valuable in that it is highly complementary to data, and can potentially help overcome data sparsity, noise, inaccuracy, etc. In this work, we propose a simple yet powerful framework that can integrate all kinds of differential equations into Gaussian processes (GPs) to enhance prediction accuracy and uncertainty quantification. These equations can be linear, nonlinear, temporal, time-spatial, complete, incomplete with unknown source terms, etc. Specifically, based on kernel differentiation, we construct a GP prior to jointly sample the values of the target function, equation-related derivatives, and latent source functions from a multivariate Gaussian distribution. The sampled values are fed to two likelihoods -- one is to fit the observations and the other to conform to the equation. We use the whitening trick to evade the strong dependency between the sampled function values and kernel parameters, and develop a stochastic variational learning algorithm. Our method shows improvement upon vanilla GPs in both simulation and several real-world applications, even using rough, incomplete equations.