FIRAL: An Active Learning Algorithm for Multinomial Logistic Regression

We investigate theory and algorithms for pool-based active learning for multiclass classification using multinomial logistic regression. Using finite sample analysis, we prove that the Fisher Information Ratio (FIR) lower and upper bounds the excess risk. Based on our theoretical analysis, we propose an active learning algorithm that employs regret minimization to minimize the FIR. To verify our derived excess risk bounds, we conduct experiments on synthetic datasets. Furthermore, we compare FIRAL with five other methods and found that our scheme outperforms them: it consistently produces the smallest classification error in the multiclass logistic regression setting, as demonstrated through experiments on MNIST, CIFAR-10, and 50-class ImageNet.

A Scalable Algorithm for Active Learning

FIRAL is a recently proposed deterministic active learning algorithm for multiclass classification using logistic regression. It was shown to outperform the state-of-the-art in terms of accuracy and robustness and comes with theoretical performance guarantees. However, its scalability suffers when dealing with datasets featuring a large number of points $n$, dimensions $d$, and classes $c$, due to its $\mathcal{O}(c^2d^2+nc^2d)$ storage and $\mathcal{O}(c^3(nd^2 + bd^3 + bn))$ computational complexity where $b$ is the number of points to select in active learning. To address these challenges, we propose an approximate algorithm with storage requirements reduced to $\mathcal{O}(n(d+c) + cd^2)$ and a computational complexity of $\mathcal{O}(bncd^2)$. Additionally, we present a parallel implementation on GPUs. We demonstrate the accuracy and scalability of our approach using MNIST, CIFAR-10, Caltech101, and ImageNet. The accuracy tests reveal no deterioration in accuracy compared to FIRAL. We report strong and weak scaling tests on up to 12 GPUs, for three million point synthetic dataset.

CLAIRE -- Parallelized Diffeomorphic Image Registration for Large-Scale Biomedical Imaging Applications

We study the performance of CLAIRE -- a diffeomorphic multi-node, multi-GPU image-registration algorithm, and software -- in large-scale biomedical imaging applications with billions of voxels. At such resolutions, most existing software packages for diffeomorphic image registration are prohibitively expensive. As a result, practitioners first significantly downsample the original images and then register them using existing tools. Our main contribution is an extensive analysis of the impact of downsampling on registration performance. We study this impact by comparing full-resolution registrations obtained with CLAIRE to lower-resolution registrations for synthetic and real-world imaging datasets. Our results suggest that registration at full resolution can yield a superior registration quality -- but not always. For example, downsampling a synthetic image from $1024^3$ to $256^3$ decreases the Dice coefficient from 92% to 79%. However, the differences are less pronounced for noisy or low-contrast high-resolution images. CLAIRE allows us not only to register images of clinically relevant size in a few seconds but also to register images at unprecedented resolution in a reasonable time. The highest resolution considered is CLARITY images of size $2816\times3016\times1162$. To the best of our knowledge, this is the first study on image registration quality at such resolutions.

ANODEV2: A Coupled Neural ODE Evolution Framework

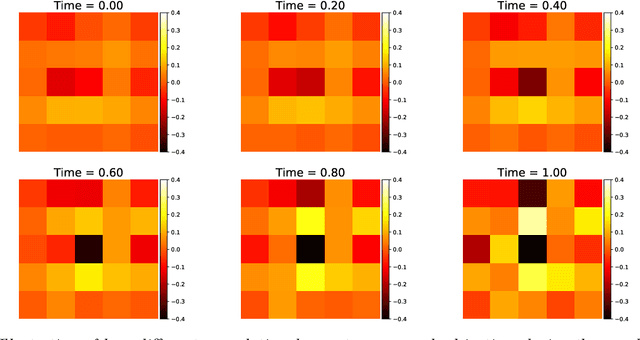
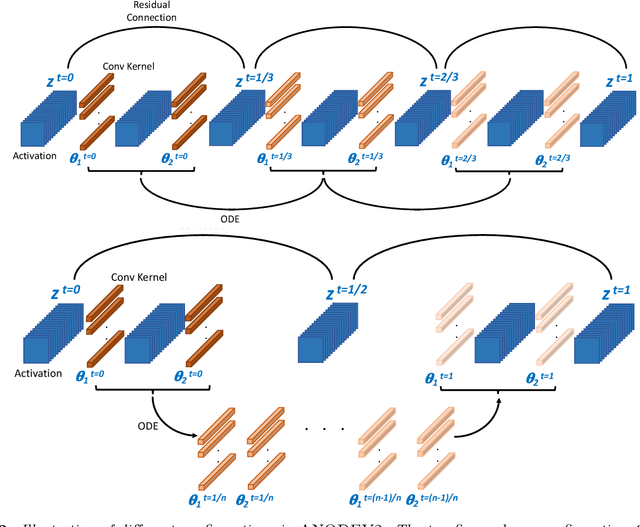
It has been observed that residual networks can be viewed as the explicit Euler discretization of an Ordinary Differential Equation (ODE). This observation motivated the introduction of so-called Neural ODEs, which allow more general discretization schemes with adaptive time stepping. Here, we propose ANODEV2, which is an extension of this approach that also allows evolution of the neural network parameters, in a coupled ODE-based formulation. The Neural ODE method introduced earlier is in fact a special case of this new more general framework. We present the formulation of ANODEV2, derive optimality conditions, and implement a coupled reaction-diffusion-advection version of this framework in PyTorch. We present empirical results using several different configurations of ANODEV2, testing them on multiple models on CIFAR-10. We report results showing that this coupled ODE-based framework is indeed trainable, and that it achieves higher accuracy, as compared to the baseline models as well as the recently-proposed Neural ODE approach.

ANODE: Unconditionally Accurate Memory-Efficient Gradients for Neural ODEs

Residual neural networks can be viewed as the forward Euler discretization of an Ordinary Differential Equation (ODE) with a unit time step. This has recently motivated researchers to explore other discretization approaches and train ODE based networks. However, an important challenge of neural ODEs is their prohibitive memory cost during gradient backpropogation. Recently a method proposed in~\verb+arXiv:1806.07366+, claimed that this memory overhead can be reduced from $\mathcal{O}(LN_t)$, where $N_t$ is the number of time steps, down to $\mathcal{O}(L)$ by solving forward ODE backwards in time, where $L$ is the depth of the network. However, we will show that this approach may lead to several problems: (i) it may be numerically unstable for ReLU/non-ReLU activations and general convolution operators, and (ii) the proposed optimize-then-discretize approach may lead to divergent training due to inconsistent gradients for small time step sizes. We discuss the underlying problems, and to address them we propose \OURS, a neural ODE framework which avoids the numerical instability related problems noted above. \OURS has a memory footprint of $\mathcal{O}(L) + \mathcal{O}(N_t)$, with the same computational cost as reversing ODE solve. We furthermore, discuss a memory efficient algorithm which can further reduce this footprint with a tradeoff of additional computational cost. We show results on Cifar-10/100 datasets using ResNet and SqueezeNext neural networks.

A Novel Domain Adaptation Framework for Medical Image Segmentation

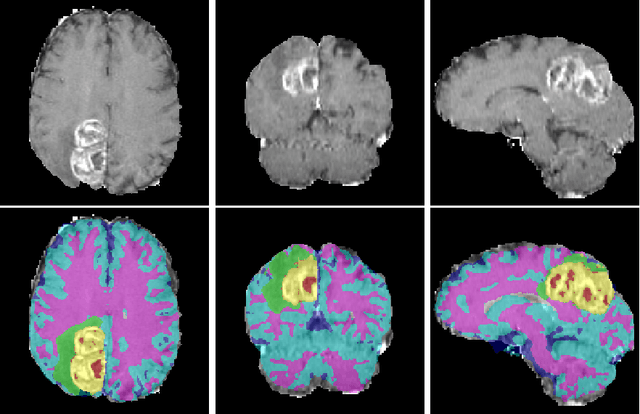
We propose a segmentation framework that uses deep neural networks and introduce two innovations. First, we describe a biophysics-based domain adaptation method. Second, we propose an automatic method to segment white and gray matter, and cerebrospinal fluid, in addition to tumorous tissue. Regarding our first innovation, we use a domain adaptation framework that combines a novel multispecies biophysical tumor growth model with a generative adversarial model to create realistic looking synthetic multimodal MR images with known segmentation. Regarding our second innovation, we propose an automatic approach to enrich available segmentation data by computing the segmentation for healthy tissues. This segmentation, which is done using diffeomorphic image registration between the BraTS training data and a set of prelabeled atlases, provides more information for training and reduces the class imbalance problem. Our overall approach is not specific to any particular neural network and can be used in conjunction with existing solutions. We demonstrate the performance improvement using a 2D U-Net for the BraTS'18 segmentation challenge. Our biophysics based domain adaptation achieves better results, as compared to the existing state-of-the-art GAN model used to create synthetic data for training.

CLAIRE: A distributed-memory solver for constrained large deformation diffeomorphic image registration

We introduce CLAIRE, a distributed-memory algorithm and software for solving constrained large deformation diffeomorphic image registration problems in three dimensions. We invert for a stationary velocity field that parameterizes the deformation map. Our solver is based on a globalized, preconditioned, inexact reduced space Gauss--Newton--Krylov scheme. We exploit state-of-the-art techniques in scientific computing to develop an effective solver that scales to thousand of distributed memory nodes on high-end clusters. Our improved, parallel implementation features parameter-, scale-, and grid-continuation schemes to speedup the computations and reduce the likelihood to get trapped in local minima. We also implement an improved preconditioner for the reduced space Hessian to speedup the convergence. We test registration performance on synthetic and real data. We demonstrate registration accuracy on 16 neuroimaging datasets. We compare the performance of our scheme against different flavors of the DEMONS algorithm for diffeomorphic image registration. We study convergence of our preconditioner and our overall algorithm. We report scalability results on state-of-the-art supercomputing platforms. We demonstrate that we can solve registration problems for clinically relevant data sizes in two to four minutes on a standard compute node with 20 cores, attaining excellent data fidelity. With the present work we achieve a speedup of (on average) 5x with a peak performance of up to 17x compared to our former work.

A Semi-Lagrangian two-level preconditioned Newton-Krylov solver for constrained diffeomorphic image registration

We propose an efficient numerical algorithm for the solution of diffeomorphic image registration problems. We use a variational formulation constrained by a partial differential equation (PDE), where the constraints are a scalar transport equation. We use a pseudospectral discretization in space and second-order accurate semi-Lagrangian time stepping scheme for the transport equations. We solve for a stationary velocity field using a preconditioned, globalized, matrix-free Newton-Krylov scheme. We propose and test a two-level Hessian preconditioner. We consider two strategies for inverting the preconditioner on the coarse grid: a nested preconditioned conjugate gradient method (exact solve) and a nested Chebyshev iterative method (inexact solve) with a fixed number of iterations. We test the performance of our solver in different synthetic and real-world two-dimensional application scenarios. We study grid convergence and computational efficiency of our new scheme. We compare the performance of our solver against our initial implementation that uses the same spatial discretization but a standard, explicit, second-order Runge-Kutta scheme for the numerical time integration of the transport equations and a single-level preconditioner. Our improved scheme delivers significant speedups over our original implementation. As a highlight, we observe a 20$\times$ speedup for a two dimensional, real world multi-subject medical image registration problem.

PDE-constrained optimization in medical image analysis

PDE-constrained optimization problems find many applications in medical image analysis, for example, neuroimaging, cardiovascular imaging, and oncological imaging. We review related literature and give examples on the formulation, discretization, and numerical solution of PDE-constrained optimization problems for medical imaging. We discuss three examples. The first one is image registration. The second one is data assimilation for brain tumor patients, and the third one data assimilation in cardiovascular imaging. The image registration problem is a classical task in medical image analysis and seeks to find pointwise correspondences between two or more images. The data assimilation problems use a PDE-constrained formulation to link a biophysical model to patient-specific data obtained from medical images. The associated optimality systems turn out to be sets of nonlinear, multicomponent PDEs that are challenging to solve in an efficient way. The ultimate goal of our work is the design of inversion methods that integrate complementary data, and rigorously follow mathematical and physical principles, in an attempt to support clinical decision making. This requires reliable, high-fidelity algorithms with a short time-to-solution. This task is complicated by model and data uncertainties, and by the fact that PDE-constrained optimization problems are ill-posed in nature, and in general yield high-dimensional, severely ill-conditioned systems after discretization. These features make regularization, effective preconditioners, and iterative solvers that, in many cases, have to be implemented on distributed-memory architectures to be practical, a prerequisite. We showcase state-of-the-art techniques in scientific computing to tackle these challenges.

Constrained $H^1$-regularization schemes for diffeomorphic image registration

We propose regularization schemes for deformable registration and efficient algorithms for their numerical approximation. We treat image registration as a variational optimal control problem. The deformation map is parametrized by its velocity. Tikhonov regularization ensures well-posedness. Our scheme augments standard smoothness regularization operators based on $H^1$- and $H^2$-seminorms with a constraint on the divergence of the velocity field, which resembles variational formulations for Stokes incompressible flows. In our formulation, we invert for a stationary velocity field and a mass source map. This allows us to explicitly control the compressibility of the deformation map and by that the determinant of the deformation gradient. We also introduce a new regularization scheme that allows us to control shear. We use a globalized, preconditioned, matrix-free, reduced space (Gauss--)Newton--Krylov scheme for numerical optimization. We exploit variable elimination techniques to reduce the number of unknowns of our system; we only iterate on the reduced space of the velocity field. Our current implementation is limited to the two-dimensional case. The numerical experiments demonstrate that we can control the determinant of the deformation gradient without compromising registration quality. This additional control allows us to avoid oversmoothing of the deformation map. We also demonstrate that we can promote or penalize shear while controlling the determinant of the deformation gradient.