A Kernel Approach for PDE Discovery and Operator Learning
Paper and Code
Oct 14, 2022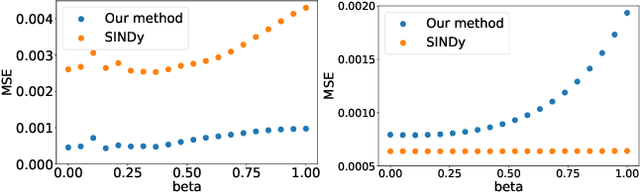


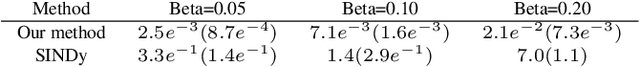
This article presents a three-step framework for learning and solving partial differential equations (PDEs) using kernel methods. Given a training set consisting of pairs of noisy PDE solutions and source/boundary terms on a mesh, kernel smoothing is utilized to denoise the data and approximate derivatives of the solution. This information is then used in a kernel regression model to learn the algebraic form of the PDE. The learned PDE is then used within a kernel based solver to approximate the solution of the PDE with a new source/boundary term, thereby constituting an operator learning framework. The proposed method is mathematically interpretable and amenable to analysis, and convenient to implement. Numerical experiments compare the method to state-of-the-art algorithms and demonstrate its superior performance on small amounts of training data and for PDEs with spatially variable coefficients.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge