Spatio-temporal Fourier Transformer (StFT) for Long-term Dynamics Prediction

Simulating the long-term dynamics of multi-scale and multi-physics systems poses a significant challenge in understanding complex phenomena across science and engineering. The complexity arises from the intricate interactions between scales and the interplay of diverse physical processes. Neural operators have emerged as promising models for predicting such dynamics due to their flexibility and computational efficiency. However, they often fail to effectively capture multi-scale interactions or quantify the uncertainties inherent in the predictions. These limitations lead to rapid error accumulation, particularly in long-term forecasting of systems characterized by complex and coupled dynamics. To address these challenges, we propose a spatio-temporal Fourier transformer (StFT), in which each transformer block is designed to learn dynamics at a specific scale. By leveraging a structured hierarchy of StFT blocks, the model explicitly captures dynamics across both macro- and micro- spatial scales. Furthermore, a generative residual correction mechanism is integrated to estimate and mitigate predictive uncertainties, enhancing both the accuracy and reliability of long-term forecasts. Evaluations conducted on three benchmark datasets (plasma, fluid, and atmospheric dynamics) demonstrate the advantages of our approach over state-of-the-art ML methods.

FTL: Transfer Learning Nonlinear Plasma Dynamic Transitions in Low Dimensional Embeddings via Deep Neural Networks

Deep learning algorithms provide a new paradigm to study high-dimensional dynamical behaviors, such as those in fusion plasma systems. Development of novel model reduction methods, coupled with detection of abnormal modes with plasma physics, opens a unique opportunity for building efficient models to identify plasma instabilities for real-time control. Our Fusion Transfer Learning (FTL) model demonstrates success in reconstructing nonlinear kink mode structures by learning from a limited amount of nonlinear simulation data. The knowledge transfer process leverages a pre-trained neural encoder-decoder network, initially trained on linear simulations, to effectively capture nonlinear dynamics. The low-dimensional embeddings extract the coherent structures of interest, while preserving the inherent dynamics of the complex system. Experimental results highlight FTL's capacity to capture transitional behaviors and dynamical features in plasma dynamics -- a task often challenging for conventional methods. The model developed in this study is generalizable and can be extended broadly through transfer learning to address various magnetohydrodynamics (MHD) modes.

AutoCT: Automated CT registration, segmentation, and quantification

The processing and analysis of computed tomography (CT) imaging is important for both basic scientific development and clinical applications. In AutoCT, we provide a comprehensive pipeline that integrates an end-to-end automatic preprocessing, registration, segmentation, and quantitative analysis of 3D CT scans. The engineered pipeline enables atlas-based CT segmentation and quantification leveraging diffeomorphic transformations through efficient forward and inverse mappings. The extracted localized features from the deformation field allow for downstream statistical learning that may facilitate medical diagnostics. On a lightweight and portable software platform, AutoCT provides a new toolkit for the CT imaging community to underpin the deployment of artificial intelligence-driven applications.

Non-intrusive Nonlinear Model Reduction via Machine Learning Approximations to Low-dimensional Operators

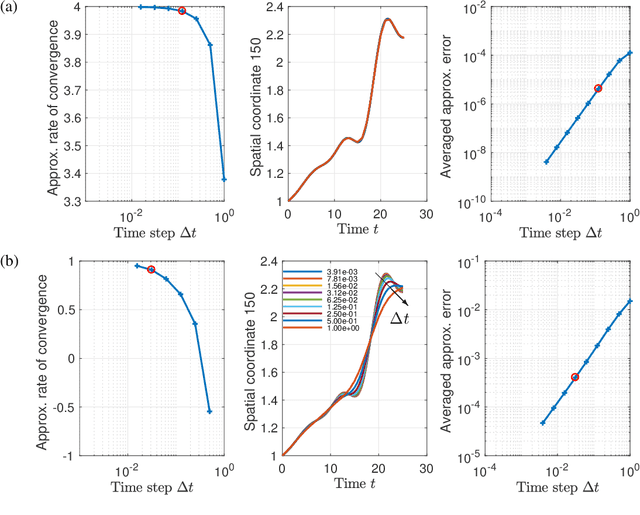
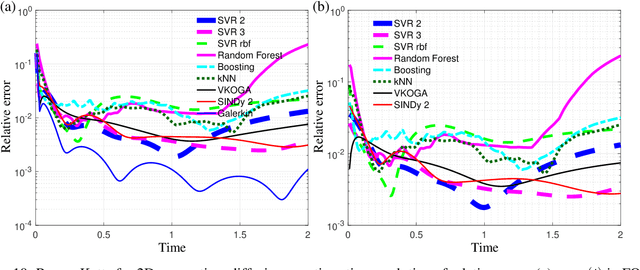
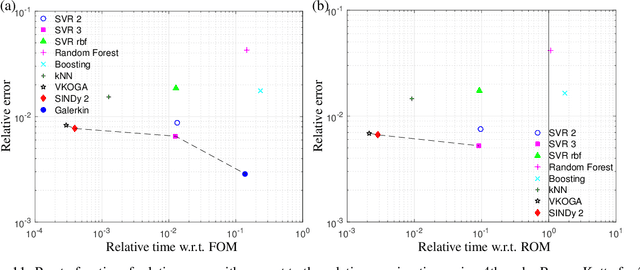
Although projection-based reduced-order models (ROMs) for parameterized nonlinear dynamical systems have demonstrated exciting results across a range of applications, their broad adoption has been limited by their intrusivity: implementing such a reduced-order model typically requires significant modifications to the underlying simulation code. To address this, we propose a method that enables traditionally intrusive reduced-order models to be accurately approximated in a non-intrusive manner. Specifically, the approach approximates the low-dimensional operators associated with projection-based reduced-order models (ROMs) using modern machine-learning regression techniques. The only requirement of the simulation code is the ability to export the velocity given the state and parameters as this functionality is used to train the approximated low-dimensional operators. In addition to enabling nonintrusivity, we demonstrate that the approach also leads to very low computational complexity, achieving up to $1000\times$ reduction in run time. We demonstrate the effectiveness of the proposed technique on two types of PDEs.