Teague Tomesh
Training Quantum Boltzmann Machines with Coresets
Jul 26, 2023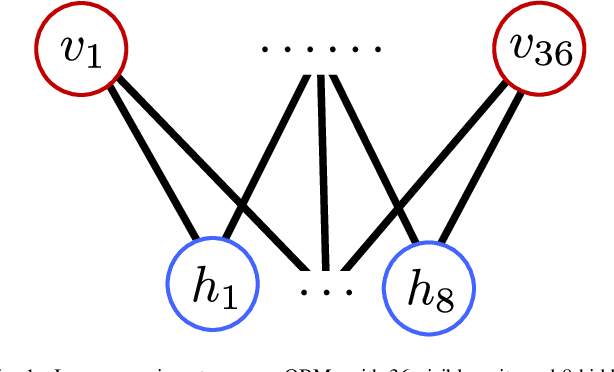
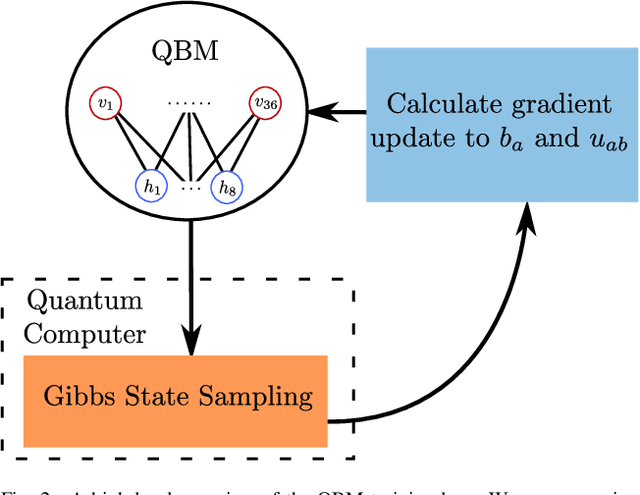
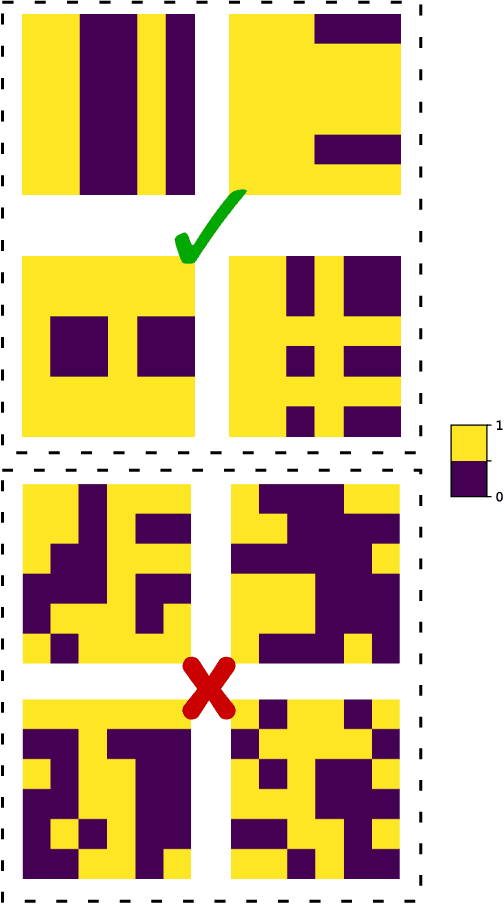
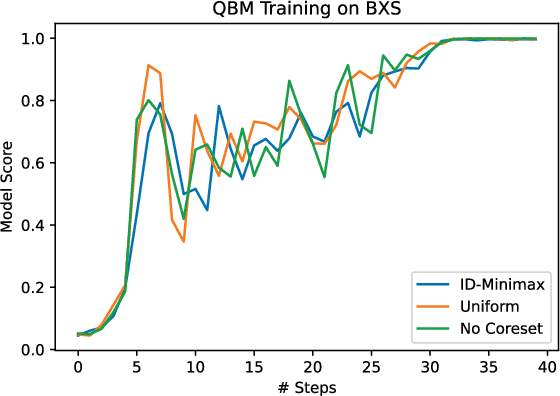
Abstract:Recent work has proposed and explored using coreset techniques for quantum algorithms that operate on classical data sets to accelerate the applicability of these algorithms on near-term quantum devices. We apply these ideas to Quantum Boltzmann Machines (QBM) where gradient-based steps which require Gibbs state sampling are the main computational bottleneck during training. By using a coreset in place of the full data set, we try to minimize the number of steps needed and accelerate the overall training time. In a regime where computational time on quantum computers is a precious resource, we propose this might lead to substantial practical savings. We evaluate this approach on 6x6 binary images from an augmented bars and stripes data set using a QBM with 36 visible units and 8 hidden units. Using an Inception score inspired metric, we compare QBM training times with and without using coresets.
Coreset Clustering on Small Quantum Computers
Apr 30, 2020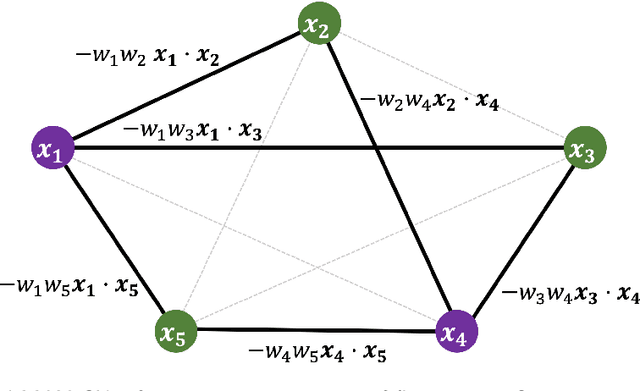
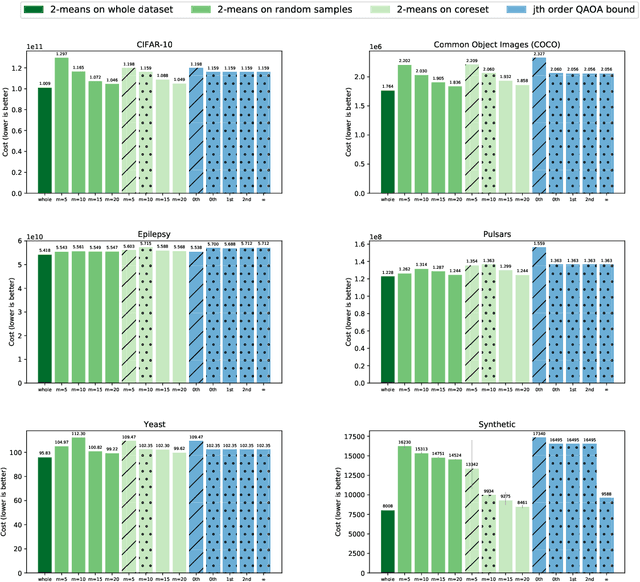
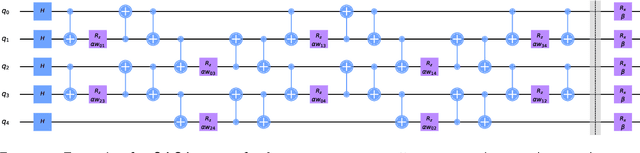
Abstract:Many quantum algorithms for machine learning require access to classical data in superposition. However, for many natural data sets and algorithms, the overhead required to load the data set in superposition can erase any potential quantum speedup over classical algorithms. Recent work by Harrow introduces a new paradigm in hybrid quantum-classical computing to address this issue, relying on coresets to minimize the data loading overhead of quantum algorithms. We investigate using this paradigm to perform $k$-means clustering on near-term quantum computers, by casting it as a QAOA optimization instance over a small coreset. We compare the performance of this approach to classical $k$-means clustering both numerically and experimentally on IBM Q hardware. We are able to find data sets where coresets work well relative to random sampling and where QAOA could potentially outperform standard $k$-means on a coreset. However, finding data sets where both coresets and QAOA work well--which is necessary for a quantum advantage over $k$-means on the entire data set--appears to be challenging.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge