A Path-Dependent Variational Framework for Incremental Information Gathering
Paper and Code
Oct 26, 2020
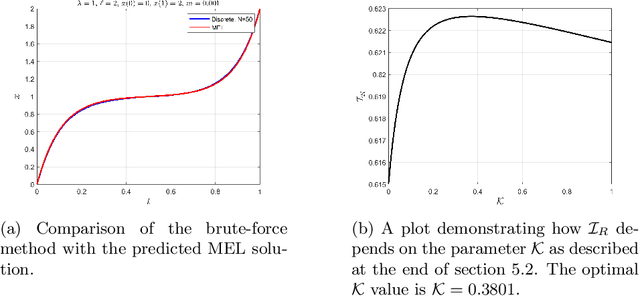
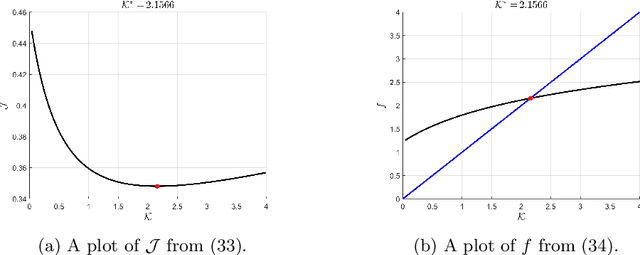
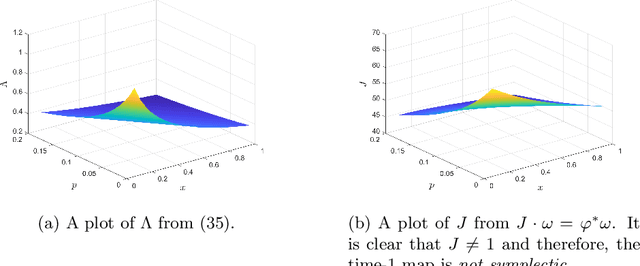
Information gathered along a path is inherently submodular; the incremental amount of information gained along a path decreases due to redundant observations. In addition to submodularity, the incremental amount of information gained is a function of not only the current state but also the entire history as well. This paper presents the construction of the first-order necessary optimality conditions for memory (history-dependent) Lagrangians. Path-dependent problems frequently appear in robotics and artificial intelligence, where the state such as a map is partially observable, and information can only be obtained along a trajectory by local sensing. Robotic exploration and environmental monitoring has numerous real-world applications and can be formulated using the proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge