Legged Robot State Estimation within Non-inertial Environments

This paper investigates the robot state estimation problem within a non-inertial environment. The proposed state estimation approach relaxes the common assumption of static ground in the system modeling. The process and measurement models explicitly treat the movement of the non-inertial environments without requiring knowledge of its motion in the inertial frame or relying on GPS or sensing environmental landmarks. Further, the proposed state estimator is formulated as an invariant extended Kalman filter (InEKF) with the deterministic part of its process model obeying the group-affine property, leading to log-linear error dynamics. The observability analysis of the filter confirms that the robot's pose (i.e., position and orientation) and velocity relative to the non-inertial environment are observable. Hardware experiments on a humanoid robot moving on a rotating and translating treadmill demonstrate the high convergence rate and accuracy of the proposed InEKF even under significant treadmill pitch sway, as well as large estimation errors.

GMKF: Generalized Moment Kalman Filter for Polynomial Systems with Arbitrary Noise

This paper develops a new filtering approach for state estimation in polynomial systems corrupted by arbitrary noise, which commonly arise in robotics. We first consider a batch setup where we perform state estimation using all data collected from the initial to the current time. We formulate the batch state estimation problem as a Polynomial Optimization Problem (POP) and relax the assumption of Gaussian noise by specifying a finite number of moments of the noise. We solve the resulting POP using a moment relaxation and prove that under suitable conditions on the rank of the relaxation, (i) we can extract a provably optimal estimate from the moment relaxation, and (ii) we can obtain a belief representation from the dual (sum-of-squares) relaxation. We then turn our attention to the filtering setup and apply similar insights to develop a GMKF for recursive state estimation in polynomial systems with arbitrary noise. The GMKF formulates the prediction and update steps as POPs and solves them using moment relaxations, carrying over a possibly non-Gaussian belief. In the linear-Gaussian case, GMKF reduces to the standard Kalman Filter. We demonstrate that GMKF performs well under highly non-Gaussian noise and outperforms common alternatives, including the Extended and Unscented Kalman Filter, and their variants on matrix Lie group.

Convex Geometric Motion Planning on Lie Groups via Moment Relaxation

This paper reports a novel result: with proper robot models on matrix Lie groups, one can formulate the kinodynamic motion planning problem for rigid body systems as \emph{exact} polynomial optimization problems that can be relaxed as semidefinite programming (SDP). Due to the nonlinear rigid body dynamics, the motion planning problem for rigid body systems is nonconvex. Existing global optimization-based methods do not properly deal with the configuration space of the 3D rigid body; thus, they do not scale well to long-horizon planning problems. We use Lie groups as the configuration space in our formulation and apply the variational integrator to formulate the forced rigid body systems as quadratic polynomials. Then we leverage Lasserre's hierarchy to obtain the globally optimal solution via SDP. By constructing the motion planning problem in a sparse manner, the results show that the proposed algorithm has \emph{linear} complexity with respect to the planning horizon. This paper demonstrates the proposed method can provide rank-one optimal solutions at relaxation order two for most of the testing cases of 1) 3D drone landing using the full dynamics model and 2) inverse kinematics for serial manipulators.

Convex Geometric Trajectory Tracking using Lie Algebraic MPC for Autonomous Marine Vehicles

Controlling marine vehicles in challenging environments is a complex task due to the presence of nonlinear hydrodynamics and uncertain external disturbances. Despite nonlinear model predictive control (MPC) showing potential in addressing these issues, its practical implementation is often constrained by computational limitations. In this paper, we propose an efficient controller for trajectory tracking of marine vehicles by employing a convex error-state MPC on the Lie group. By leveraging the inherent geometric properties of the Lie group, we can construct globally valid error dynamics and formulate a quadratic programming-based optimization problem. Our proposed MPC demonstrates effectiveness in trajectory tracking through extensive-numerical simulations, including scenarios involving ocean currents. Notably, our method substantially reduces computation time compared to nonlinear MPC, making it well-suited for real-time control applications with long prediction horizons or involving small marine vehicles.

Fully Proprioceptive Slip-Velocity-Aware State Estimation for Mobile Robots via Invariant Kalman Filtering and Disturbance Observer

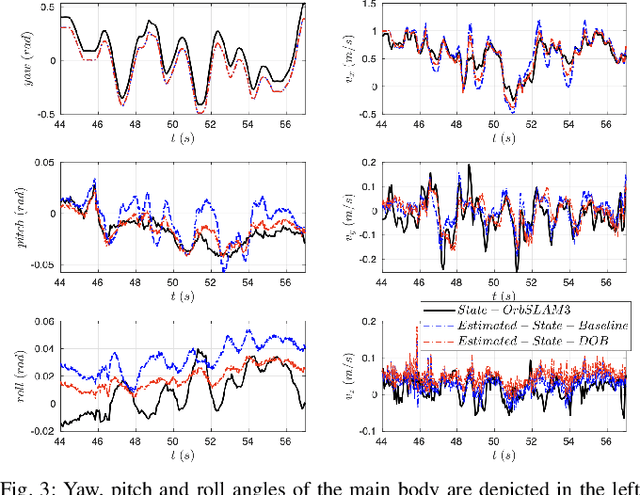
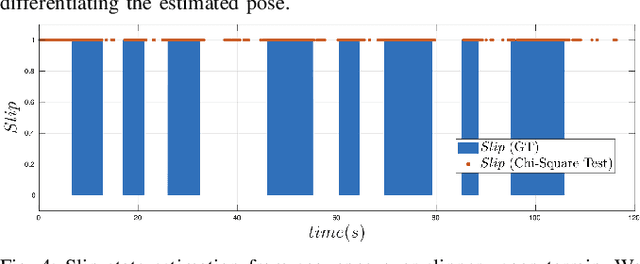
This paper develops a novel slip estimator using the invariant observer design theory and Disturbance Observer (DOB). The proposed state estimator for mobile robots is fully proprioceptive and combines data from an inertial measurement unit and body velocity within a Right Invariant Extended Kalman Filter (RI-EKF). By embedding the slip velocity into $\mathrm{SE}_3(3)$ Lie group, the developed DOB-based RI-EKF provides real-time accurate velocity and slip velocity estimates on different terrains. Experimental results using a Husky wheeled robot confirm the mathematical derivations and show better performance than a standard RI-EKF baseline. Open source software is available for download and reproducing the presented results.

Lie Algebraic Cost Function Design for Control on Lie Groups

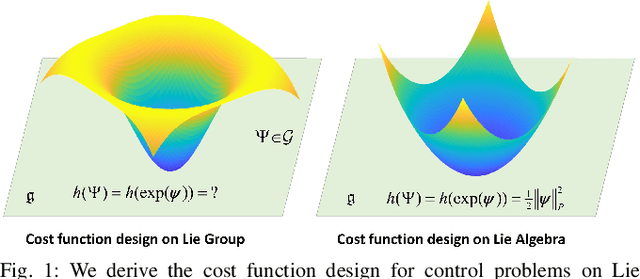
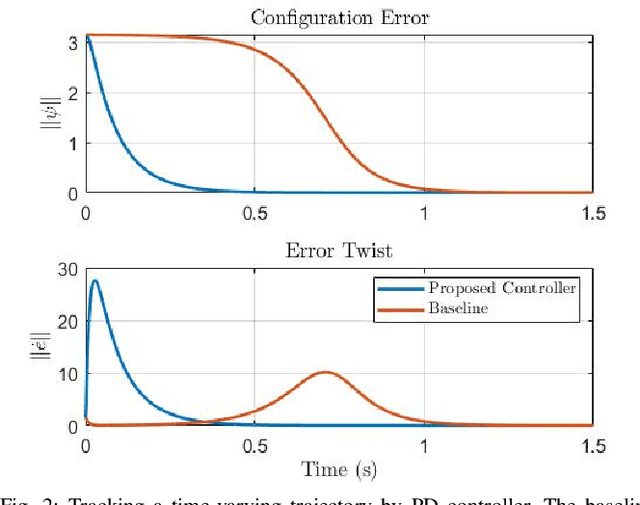
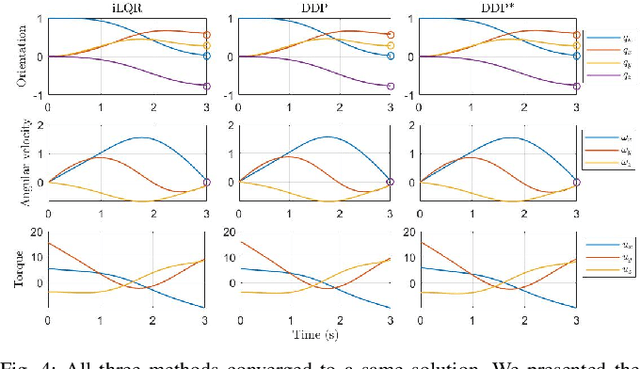
This paper presents a control framework on Lie groups by designing the control objective in its Lie algebra. Control on Lie groups is challenging due to its nonlinear nature and difficulties in system parameterization. Existing methods to design the control objective on a Lie group and then derive the gradient for controller design are non-trivial and can result in slow convergence in tracking control. We show that with a proper left-invariant metric, setting the gradient of the cost function as the tracking error in the Lie algebra leads to a quadratic Lyapunov function that enables globally exponential convergence. In the PD control case, we show that our controller can maintain an exponential convergence rate even when the initial error is approaching $\pi$ in SO(3). We also show the merit of this proposed framework in trajectory optimization. The proposed cost function enables the iterative Linear Quadratic Regulator (iLQR) to converge much faster than the Differential Dynamic Programming (DDP) with a well-adopted cost function when the initial trajectory is poorly initialized on SO(3).

Input Influence Matrix Design for MIMO Discrete-Time Ultra-Local Model

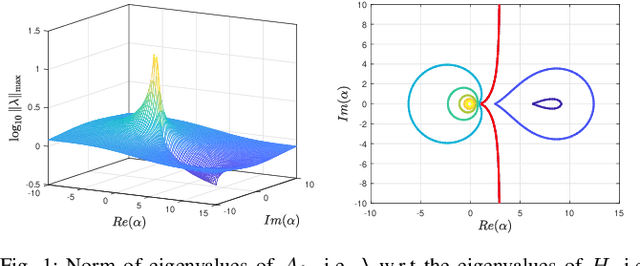
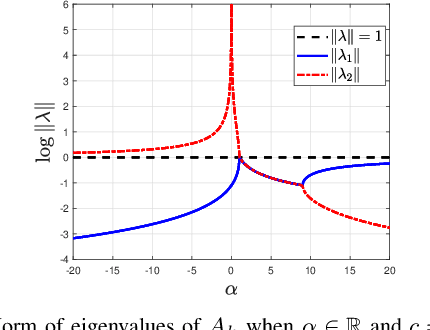
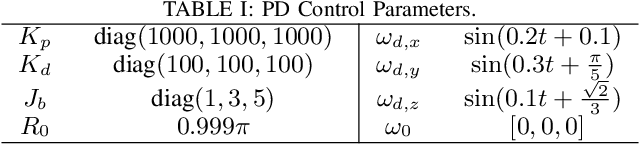
Ultra-Local Models (ULM) have been applied to perform model-free control of nonlinear systems with unknown or partially known dynamics. Unfortunately, extending these methods to MIMO systems requires designing a dense input influence matrix which is challenging. This paper presents guidelines for designing an input influence matrix for discrete-time, control-affine MIMO systems using an ULM-based controller. This paper analyzes the case that uses ULM and a model-free control scheme: the H\"older-continuous Finite-Time Stable (FTS) control. By comparing the ULM with the actual system dynamics, the paper describes how to extract the input-dependent part from the lumped ULM dynamics and finds that the tracking and state estimation error are coupled. The stability of the ULM-FTS error dynamics is affected by the eigenvalues of the difference (defined by matrix multiplication) between the actual and designed input influence matrix. Finally, the paper shows that a wide range of input influence matrix designs can keep the ULM-FTS error dynamics (at least locally) asymptotically stable. A numerical simulation is included to verify the result. The analysis can also be extended to other ULM-based controllers.

An Error-State Model Predictive Control on Connected Matrix Lie Groups for Legged Robot Control

This paper reports on a new error-state Model Predictive Control (MPC) approach on connected matrix Lie groups for robot control. The linearized tracking error dynamics and the linearized equations of motion are derived in the Lie algebra. Moreover, given an initial condition, the linearized tracking error dynamics and equations of motion are globally valid and evolve independently of the system trajectory. By exploiting the symmetry of the problem, the proposed approach shows faster convergence of rotation and position simultaneously than the state-of-the-art geometric variational MPC based on variational-based linearization. Numerical simulation on tracking control of a fully-actuated 3D rigid body dynamics confirms the benefits of the proposed approach compared to the baselines. Furthermore, the proposed MPC is also verified in pose control and locomotion experiments on a quadrupedal robot MIT Mini Cheetah.

Legged Robot State Estimation in Slippery Environments Using Invariant Extended Kalman Filter with Velocity Update

This paper proposes a state estimator for legged robots operating in slippery environments. An Invariant Extended Kalman Filter (InEKF) is implemented to fuse inertial and velocity measurements from a tracking camera and leg kinematic constraints. {\color{black}The misalignment between the camera and the robot-frame is also modeled thus enabling auto-calibration of camera pose.} The leg kinematics based velocity measurement is formulated as a right-invariant observation. Nonlinear observability analysis shows that other than the rotation around the gravity vector and the absolute position, all states are observable except for some singular cases. Discrete observability analysis demonstrates that our filter is consistent with the underlying nonlinear system. An online noise parameter tuning method is developed to adapt to the highly time-varying camera measurement noise. The proposed method is experimentally validated on a Cassie bipedal robot walking over slippery terrain. A video for the experiment can be found at https://youtu.be/VIqJL0cUr7s.

Toward Safety-Aware Informative Motion Planning for Legged Robots

This paper reports on developing an integrated framework for safety-aware informative motion planning suitable for legged robots. The information-gathering planner takes a dense stochastic map of the environment into account, while safety constraints are enforced via Control Barrier Functions (CBFs). The planner is based on the Incrementally-exploring Information Gathering (IIG) algorithm and allows closed-loop kinodynamic node expansion using a Model Predictive Control (MPC) formalism. Robotic exploration and information gathering problems are inherently path-dependent problems. That is, the information collected along a path depends on the state and observation history. As such, motion planning solely based on a modular cost does not lead to suitable plans for exploration. We propose SAFE-IIG, an integrated informative motion planning algorithm that takes into account: 1) a robot's perceptual field of view via a submodular information function computed over a stochastic map of the environment, 2) a robot's dynamics and safety constraints via discrete-time CBFs and MPC for closed-loop multi-horizon node expansions, and 3) an automatic stopping criterion via setting an information-theoretic planning horizon. The simulation results show that SAFE-IIG can plan a safe and dynamically feasible path while exploring a dense map.