Learning the Rolling Penny Dynamics

We consider learning the dynamics of a typical nonholonomic system -- the rolling penny. A nonholonomic system is a system subject to nonholonomic constraints. Unlike holonomic constraints, a nonholonomic constraint does not define a submanifold on the configuration space. Therefore, the inverse problem of finding the constraints has to involve the tangent space. This paper discuss how to learn the dynamics, as well as the constraints for such a system given the data set of discrete trajectories on the tangent bundle $TQ$.

The Interplay Between Symmetries and Impact Effects on Hybrid Mechanical Systems

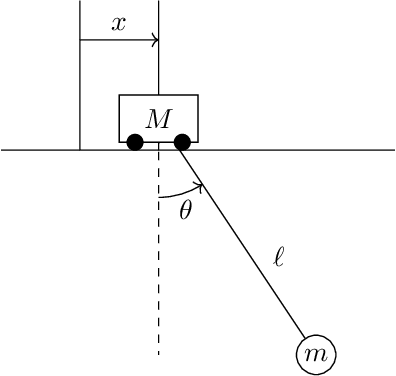
Hybrid systems are dynamical systems with continuous-time and discrete-time components in their dynamics. When hybrid systems are defined on a principal bundle we are able to define two classes of impacts for the discrete-time transition of the dynamics: interior impacts and exterior impacts. In this paper we define hybrid systems on principal bundles, study the underlying geometry on the switching surface where impacts occur and we find conditions for which both exterior and interior impacts are preserved by the mechanical connection induced in the principal bundle.

Lie Algebraic Cost Function Design for Control on Lie Groups

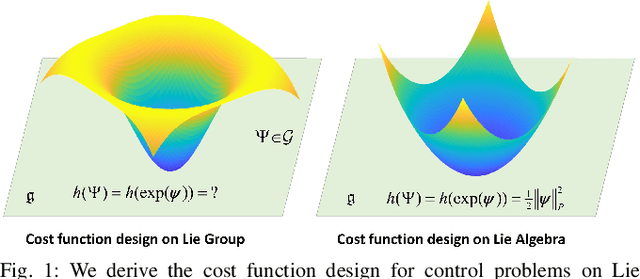
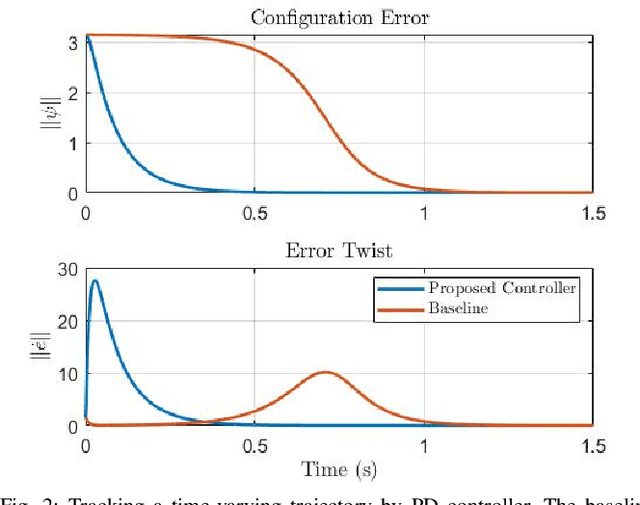
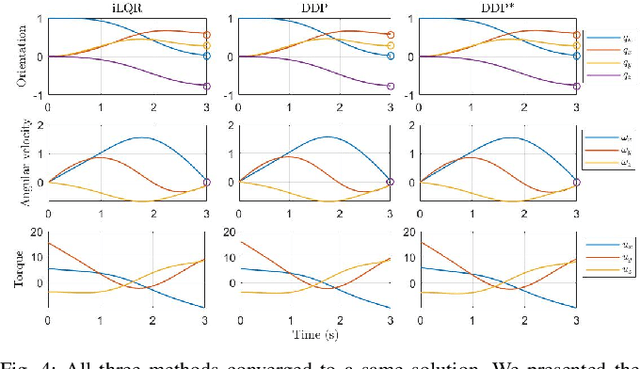
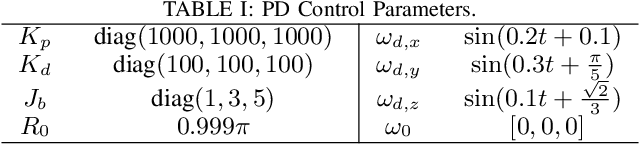
This paper presents a control framework on Lie groups by designing the control objective in its Lie algebra. Control on Lie groups is challenging due to its nonlinear nature and difficulties in system parameterization. Existing methods to design the control objective on a Lie group and then derive the gradient for controller design are non-trivial and can result in slow convergence in tracking control. We show that with a proper left-invariant metric, setting the gradient of the cost function as the tracking error in the Lie algebra leads to a quadratic Lyapunov function that enables globally exponential convergence. In the PD control case, we show that our controller can maintain an exponential convergence rate even when the initial error is approaching $\pi$ in SO(3). We also show the merit of this proposed framework in trajectory optimization. The proposed cost function enables the iterative Linear Quadratic Regulator (iLQR) to converge much faster than the Differential Dynamic Programming (DDP) with a well-adopted cost function when the initial trajectory is poorly initialized on SO(3).

Input Influence Matrix Design for MIMO Discrete-Time Ultra-Local Model

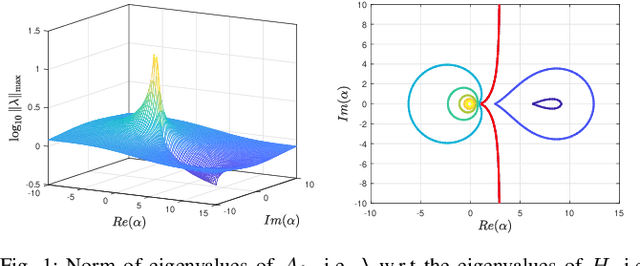
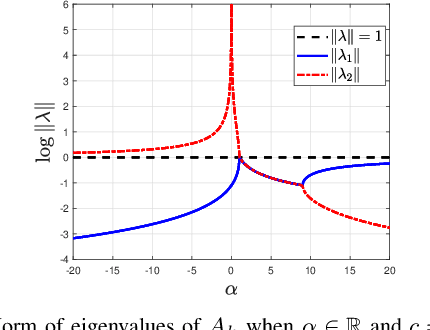
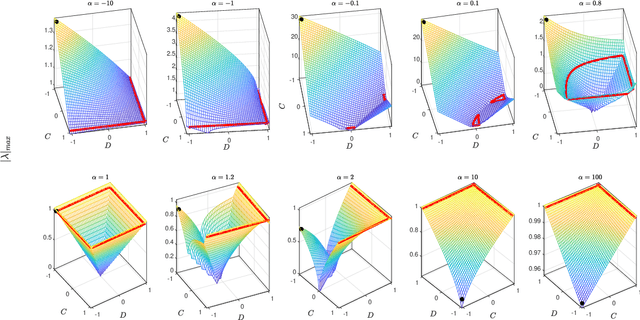
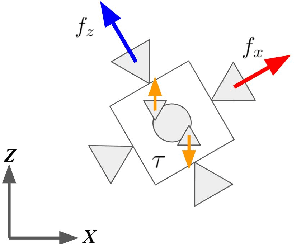
Ultra-Local Models (ULM) have been applied to perform model-free control of nonlinear systems with unknown or partially known dynamics. Unfortunately, extending these methods to MIMO systems requires designing a dense input influence matrix which is challenging. This paper presents guidelines for designing an input influence matrix for discrete-time, control-affine MIMO systems using an ULM-based controller. This paper analyzes the case that uses ULM and a model-free control scheme: the H\"older-continuous Finite-Time Stable (FTS) control. By comparing the ULM with the actual system dynamics, the paper describes how to extract the input-dependent part from the lumped ULM dynamics and finds that the tracking and state estimation error are coupled. The stability of the ULM-FTS error dynamics is affected by the eigenvalues of the difference (defined by matrix multiplication) between the actual and designed input influence matrix. Finally, the paper shows that a wide range of input influence matrix designs can keep the ULM-FTS error dynamics (at least locally) asymptotically stable. A numerical simulation is included to verify the result. The analysis can also be extended to other ULM-based controllers.

Nonparametric Continuous Sensor Registration

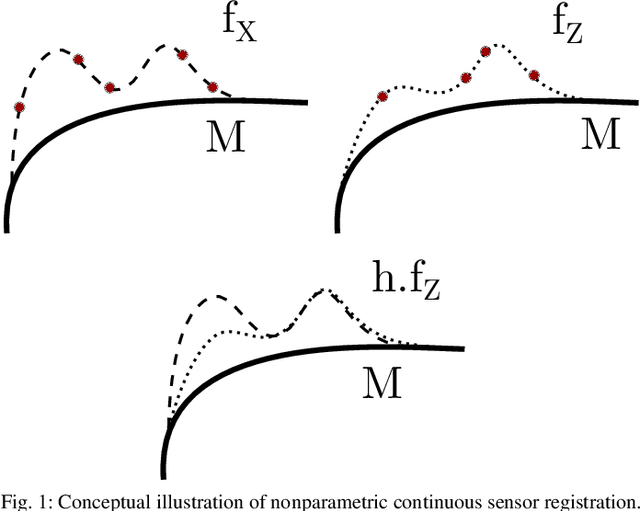
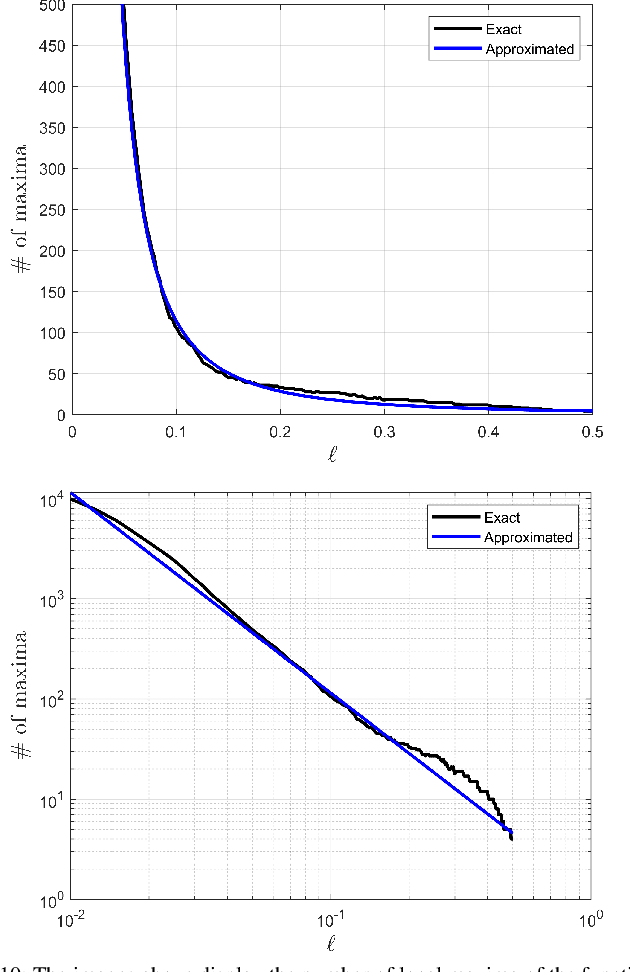
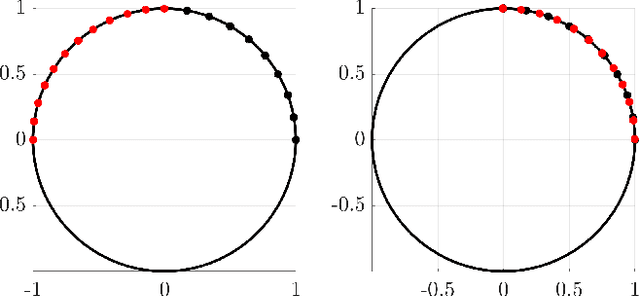
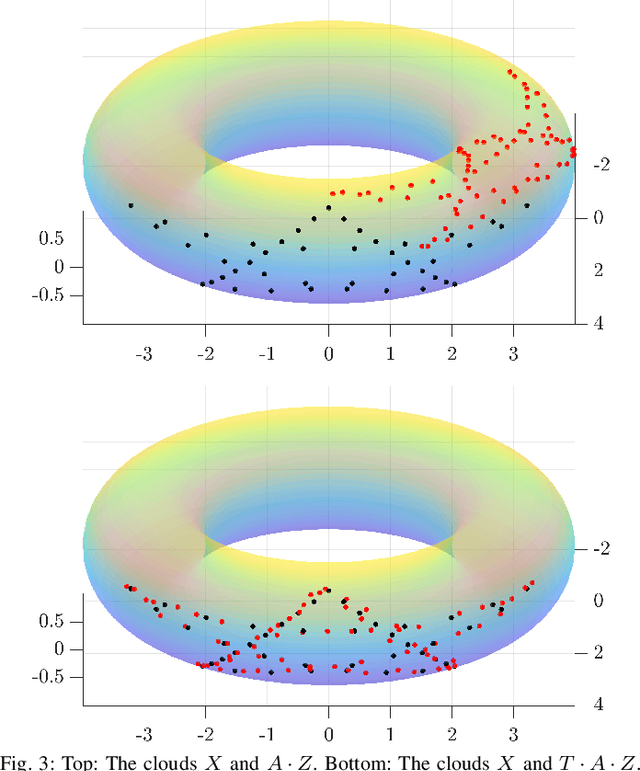
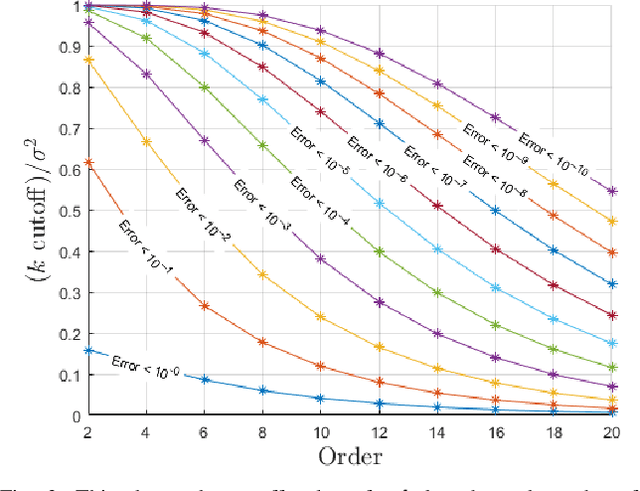
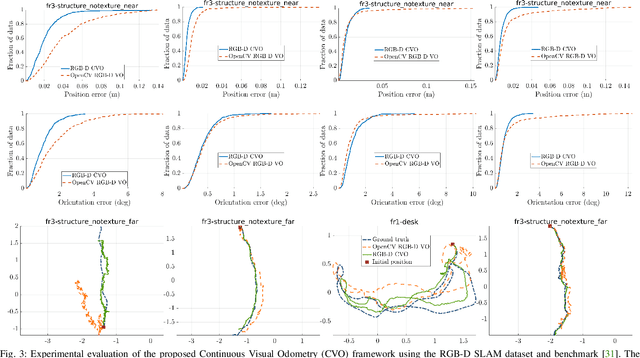
This paper develops a new mathematical framework that enables nonparametric joint semantic/appearance and geometric representation of continuous functions using data. The joint semantic and geometric embedding is modeled by representing the processes in a reproducing kernel Hilbert space. The framework allows the functions to be defined on arbitrary smooth manifolds where the action of a Lie group is used to align them. The continuous functions allow the registration to be independent of a specific signal resolution and the framework is fully analytical with a closed-form derivation of the Riemannian gradient and Hessian. We study a more specialized but widely used case where the Lie group acts on functions isometrically. We solve the problem by maximizing the inner product between two functions defined over data, while the continuous action of the rigid body motion Lie group is captured through the integration of the flow in the corresponding Lie algebra. Low-dimensional cases are derived with numerical examples to show the generality of the proposed framework. The high-dimensional derivation for the special Euclidean group acting on the Euclidean space showcases the point cloud registration and bird's-eye view map registration abilities. A specific derivation and implementation of this framework for RGB-D cameras outperform the state-of-the-art robust visual odometry and performs well in texture and structure-scares environments.

Adaptive Continuous Visual Odometry from RGB-D Images

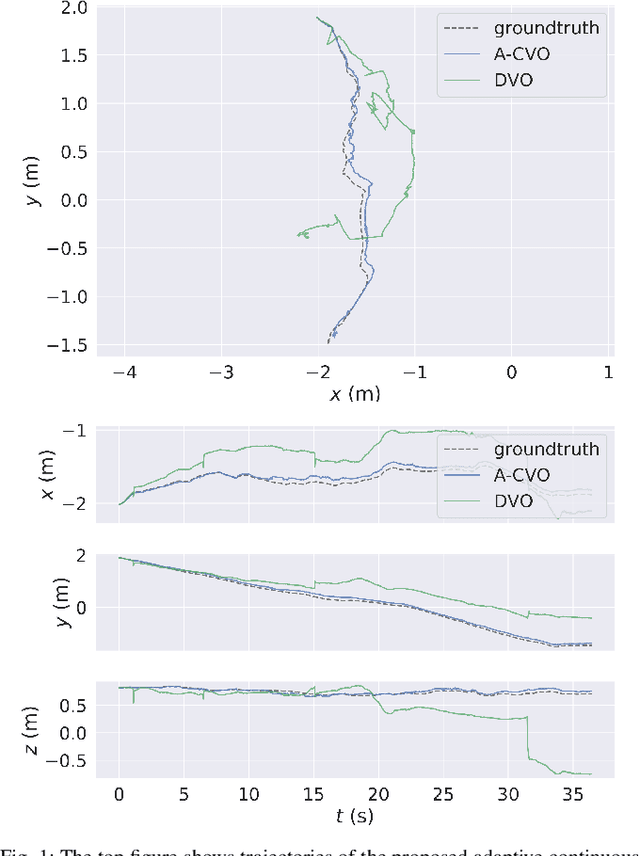
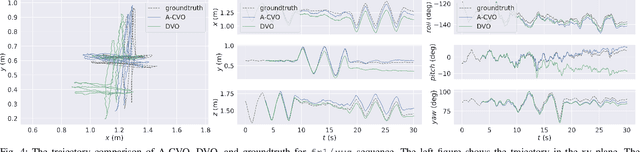
In this paper, we extend the recently developed continuous visual odometry framework for RGB-D cameras to an adaptive framework via online hyperparameter learning. We focus on the case of isotropic kernels with a scalar as the length-scale. In practice and as expected, the length-scale has remarkable impacts on the performance of the original framework. Previously it was handled using a fixed set of conditions within the solver to reduce the length-scale as the algorithm reaches a local minimum. We automate this process by a greedy gradient descent step at each iteration to find the next-best length-scale. Furthermore, to handle failure cases in the gradient descent step where the gradient is not well-behaved, such as the absence of structure or texture in the scene, we use a search interval for the length-scale and guide it gradually toward the smaller values. This latter strategy reverts the adaptive framework to the original setup. The experimental evaluations using publicly available RGB-D benchmarks show the proposed adaptive continuous visual odometry outperforms the original framework and the current state-of-the-art. We also make the software for the developed algorithm publicly available.

Continuous Direct Sparse Visual Odometry from RGB-D Images

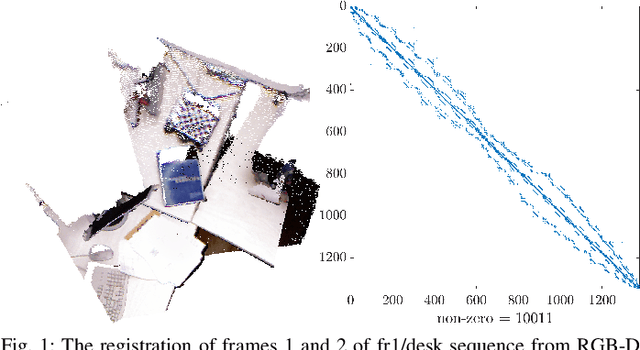
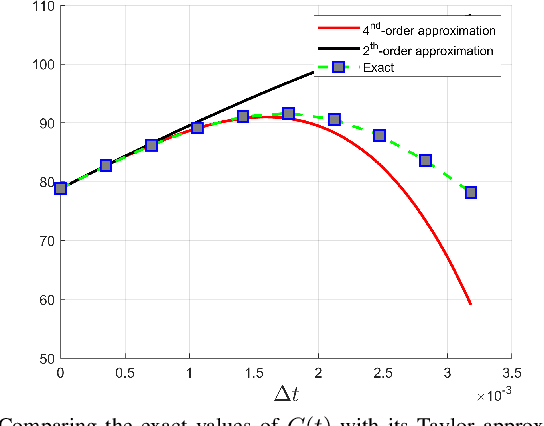
This paper reports on a novel formulation and evaluation of visual odometry from RGB-D images. Assuming a static scene, the developed theoretical framework generalizes the widely used direct energy formulation (photometric error minimization) technique for obtaining a rigid body transformation that aligns two overlapping RGB-D images to a continuous formulation. The continuity is achieved through functional treatment of the problem and representing the process models over RGB-D images in a reproducing kernel Hilbert space; consequently, the registration is not limited to the specific image resolution and the framework is fully analytical with a closed-form derivation of the gradient. We solve the problem by maximizing the inner product between two functions defined over RGB-D images, while the continuous action of the rigid body motion Lie group is captured through the integration of the flow in the corresponding Lie algebra. Energy-based approaches have been extremely successful and the developed framework in this paper shares many of their desired properties such as the parallel structure on both CPUs and GPUs, sparsity, semi-dense tracking, avoiding explicit data association which is computationally expensive, and possible extensions to the simultaneous localization and mapping frameworks. The evaluations on experimental data and comparison with the equivalent energy-based formulation of the problem confirm the effectiveness of the proposed technique, especially, when the lack of structure and texture in the environment is evident.