Nonparametric Continuous Sensor Registration

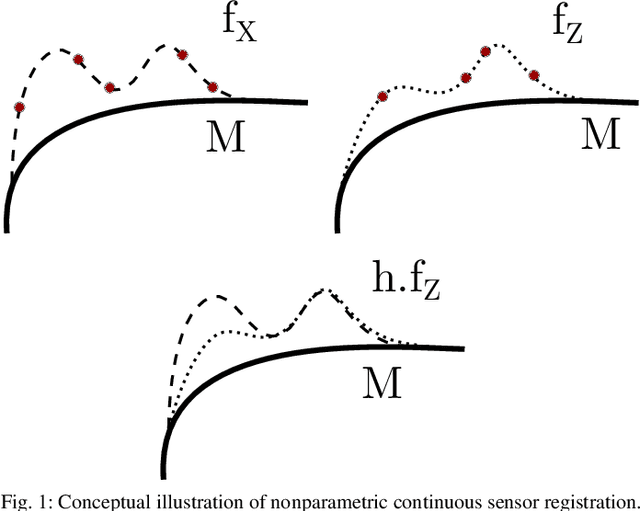
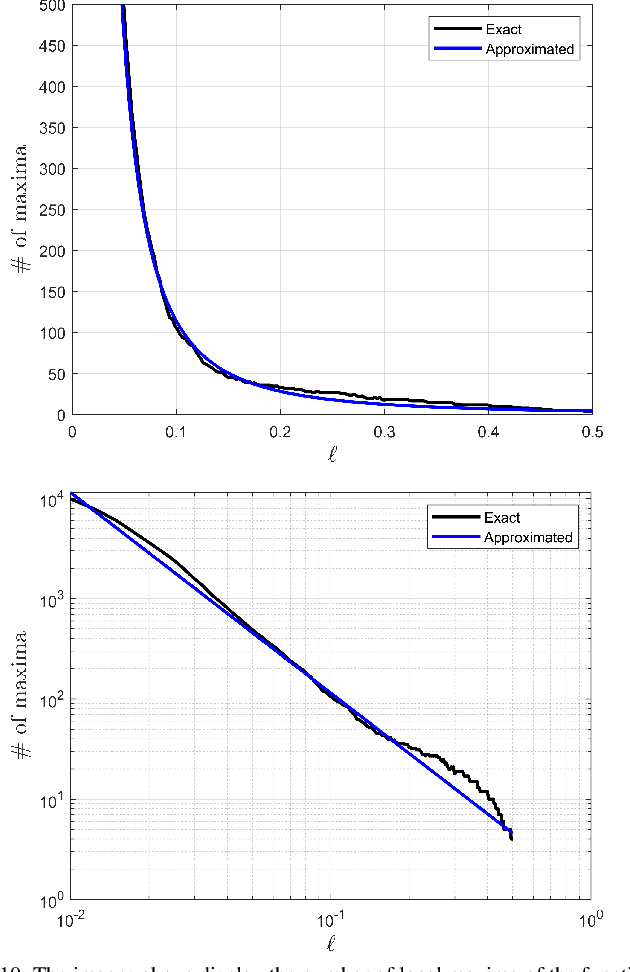
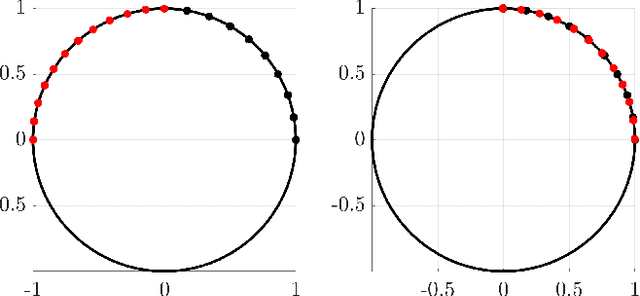
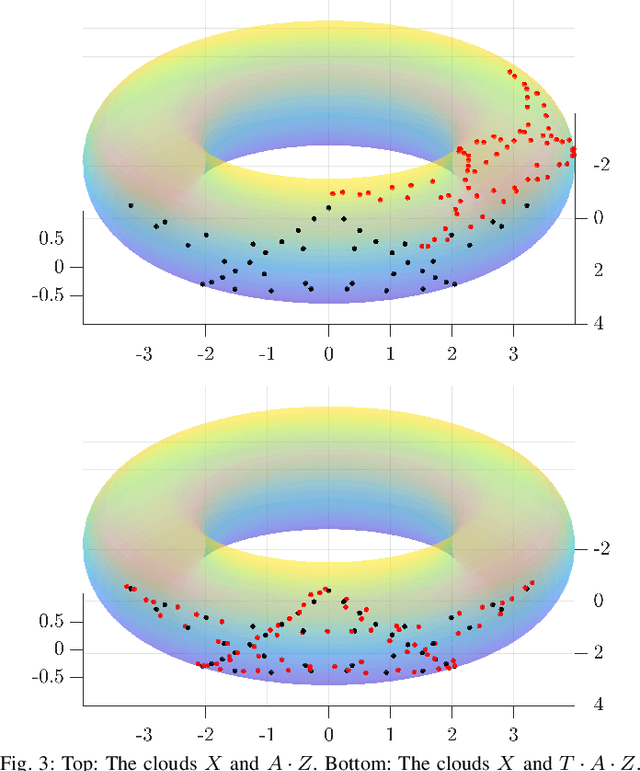
This paper develops a new mathematical framework that enables nonparametric joint semantic/appearance and geometric representation of continuous functions using data. The joint semantic and geometric embedding is modeled by representing the processes in a reproducing kernel Hilbert space. The framework allows the functions to be defined on arbitrary smooth manifolds where the action of a Lie group is used to align them. The continuous functions allow the registration to be independent of a specific signal resolution and the framework is fully analytical with a closed-form derivation of the Riemannian gradient and Hessian. We study a more specialized but widely used case where the Lie group acts on functions isometrically. We solve the problem by maximizing the inner product between two functions defined over data, while the continuous action of the rigid body motion Lie group is captured through the integration of the flow in the corresponding Lie algebra. Low-dimensional cases are derived with numerical examples to show the generality of the proposed framework. The high-dimensional derivation for the special Euclidean group acting on the Euclidean space showcases the point cloud registration and bird's-eye view map registration abilities. A specific derivation and implementation of this framework for RGB-D cameras outperform the state-of-the-art robust visual odometry and performs well in texture and structure-scares environments.