Learning the Rolling Penny Dynamics

We consider learning the dynamics of a typical nonholonomic system -- the rolling penny. A nonholonomic system is a system subject to nonholonomic constraints. Unlike holonomic constraints, a nonholonomic constraint does not define a submanifold on the configuration space. Therefore, the inverse problem of finding the constraints has to involve the tangent space. This paper discuss how to learn the dynamics, as well as the constraints for such a system given the data set of discrete trajectories on the tangent bundle $TQ$.

Can't Touch This: Real-Time, Safe Motion Planning and Control for Manipulators Under Uncertainty

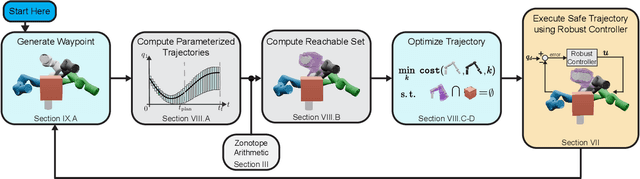
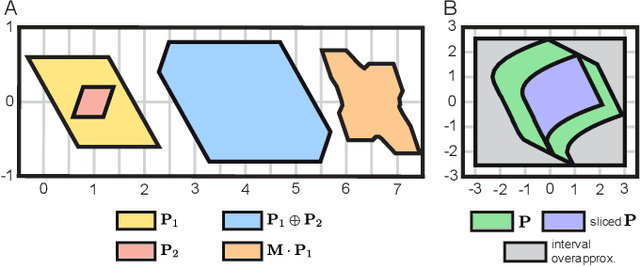
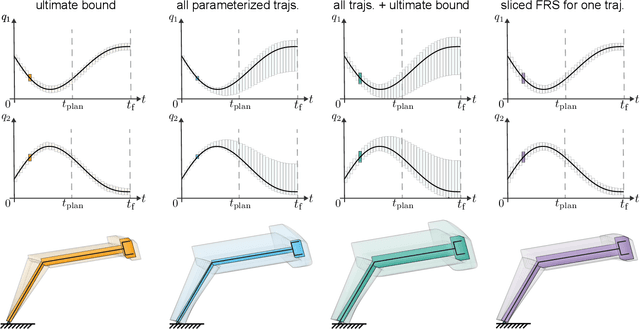
A key challenge to the widespread deployment of robotic manipulators is the need to ensure safety in arbitrary environments while generating new motion plans in real-time. In particular, one must ensure that a manipulator does not collide with obstacles, collide with itself, or exceed its joint torque limits. This challenge is compounded by the need to account for uncertainty in the mass and inertia of manipulated objects, and potentially the robot itself. The present work addresses this challenge by proposing Autonomous Robust Manipulation via Optimization with Uncertainty-aware Reachability (ARMOUR), a provably-safe, receding-horizon trajectory planner and tracking controller framework for serial link manipulators. ARMOUR works by first constructing a robust, passivity-based controller that is proven to enable a manipulator to track desired trajectories with bounded error despite uncertain dynamics. Next, ARMOUR uses a novel variation on the Recursive Newton-Euler Algorithm (RNEA) to compute the set of all possible inputs required to track any trajectory within a continuum of desired trajectories. Finally, the method computes an over-approximation to the swept volume of the manipulator; this enables one to formulate an optimization problem, which can be solved in real-time, to synthesize provably-safe motion. The proposed method is compared to state of the art methods and demonstrated on a variety of challenging manipulation examples in simulation and on real hardware, such as maneuvering a dumbbell with uncertain mass around obstacles.