Phasing Through the Flames: Rapid Motion Planning with the AGHF PDE for Arbitrary Objective Functions and Constraints

The generation of optimal trajectories for high-dimensional robotic systems under constraints remains computationally challenging due to the need to simultaneously satisfy dynamic feasibility, input limits, and task-specific objectives while searching over high-dimensional spaces. Recent approaches using the Affine Geometric Heat Flow (AGHF) Partial Differential Equation (PDE) have demonstrated promising results, generating dynamically feasible trajectories for complex systems like the Digit V3 humanoid within seconds. These methods efficiently solve trajectory optimization problems over a two-dimensional domain by evolving an initial trajectory to minimize control effort. However, these AGHF approaches are limited to a single type of optimal control problem (i.e., minimizing the integral of squared control norms) and typically require initial guesses that satisfy constraints to ensure satisfactory convergence. These limitations restrict the potential utility of the AGHF PDE especially when trying to synthesize trajectories for robotic systems. This paper generalizes the AGHF formulation to accommodate arbitrary cost functions, significantly expanding the classes of trajectories that can be generated. This work also introduces a Phase1 - Phase 2 Algorithm that enables the use of constraint-violating initial guesses while guaranteeing satisfactory convergence. The effectiveness of the proposed method is demonstrated through comparative evaluations against state-of-the-art techniques across various dynamical systems and challenging trajectory generation problems. Project Page: https://roahmlab.github.io/BLAZE/

Provably-Safe, Online System Identification

Precise manipulation tasks require accurate knowledge of payload inertial parameters. Unfortunately, identifying these parameters for unknown payloads while ensuring that the robotic system satisfies its input and state constraints while avoiding collisions with the environment remains a significant challenge. This paper presents an integrated framework that enables robotic manipulators to safely and automatically identify payload parameters while maintaining operational safety guarantees. The framework consists of two synergistic components: an online trajectory planning and control framework that generates provably-safe exciting trajectories for system identification that can be tracked while respecting robot constraints and avoiding obstacles and a robust system identification method that computes rigorous overapproximative bounds on end-effector inertial parameters assuming bounded sensor noise. Experimental validation on a robotic manipulator performing challenging tasks with various unknown payloads demonstrates the framework's effectiveness in establishing accurate parameter bounds while maintaining safety throughout the identification process. The code is available at our project webpage: https://roahmlab.github.io/OnlineSafeSysID/.

DEFT: Differentiable Branched Discrete Elastic Rods for Modeling Furcated DLOs in Real-Time

Autonomous wire harness assembly requires robots to manipulate complex branched cables with high precision and reliability. A key challenge in automating this process is predicting how these flexible and branched structures behave under manipulation. Without accurate predictions, it is difficult for robots to reliably plan or execute assembly operations. While existing research has made progress in modeling single-threaded Deformable Linear Objects (DLOs), extending these approaches to Branched Deformable Linear Objects (BDLOs) presents fundamental challenges. The junction points in BDLOs create complex force interactions and strain propagation patterns that cannot be adequately captured by simply connecting multiple single-DLO models. To address these challenges, this paper presents Differentiable discrete branched Elastic rods for modeling Furcated DLOs in real-Time (DEFT), a novel framework that combines a differentiable physics-based model with a learning framework to: 1) accurately model BDLO dynamics, including dynamic propagation at junction points and grasping in the middle of a BDLO, 2) achieve efficient computation for real-time inference, and 3) enable planning to demonstrate dexterous BDLO manipulation. A comprehensive series of real-world experiments demonstrates DEFT's efficacy in terms of accuracy, computational speed, and generalizability compared to state-of-the-art alternatives. Project page:https://roahmlab.github.io/DEFT/.

Bring the Heat: Rapid Trajectory Optimization with Pseudospectral Techniques and the Affine Geometric Heat Flow Equation

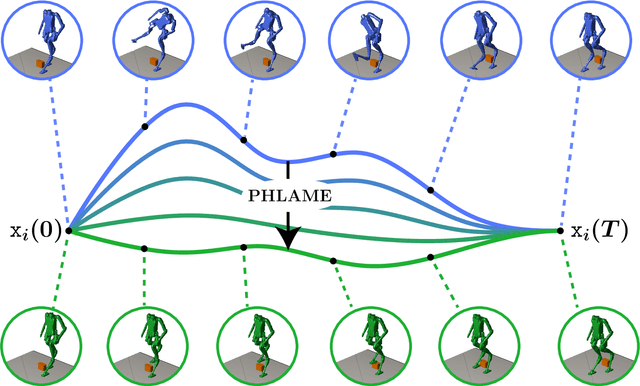
Generating optimal trajectories for high-dimensional robotic systems in a time-efficient manner while adhering to constraints is a challenging task. To address this challenge, this paper introduces PHLAME, which applies pseudospectral collocation and spatial vector algebra to efficiently solve the Affine Geometric Heat Flow (AGHF) Partial Differential Equation (PDE) for trajectory optimization. Unlike traditional PDE approaches like the Hamilton-Jacobi-Bellman (HJB) PDE, which solve for a function over the entire state space, computing a solution to the AGHF PDE scales more efficiently because its solution is defined over a two-dimensional domain, thereby avoiding the intractability of state-space scaling. To solve the AGHF one usually applies the Method of Lines (MOL), which works by discretizing one variable of the AGHF PDE, effectively converting the PDE into a system of ordinary differential equations (ODEs) that can be solved using standard time-integration methods. Though powerful, this method requires a fine discretization to generate accurate solutions and still requires evaluating the AGHF PDE which can be computationally expensive for high-dimensional systems. PHLAME overcomes this deficiency by using a pseudospectral method, which reduces the number of function evaluations required to yield a high accuracy solution thereby allowing it to scale efficiently to high-dimensional robotic systems. To further increase computational speed, this paper presents analytical expressions for the AGHF and its Jacobian, both of which can be computed efficiently using rigid body dynamics algorithms. The proposed method PHLAME is tested across various dynamical systems, with and without obstacles and compared to a number of state-of-the-art techniques. PHLAME generates trajectories for a 44-dimensional state-space system in $\sim3$ seconds, much faster than current state-of-the-art techniques.

Conformalized Reachable Sets for Obstacle Avoidance With Spheres

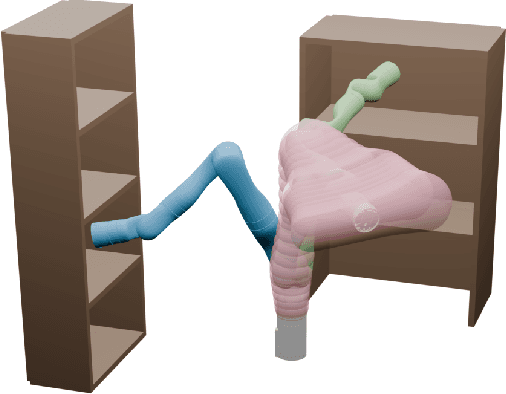
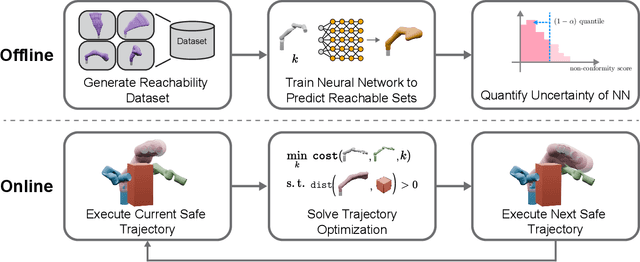
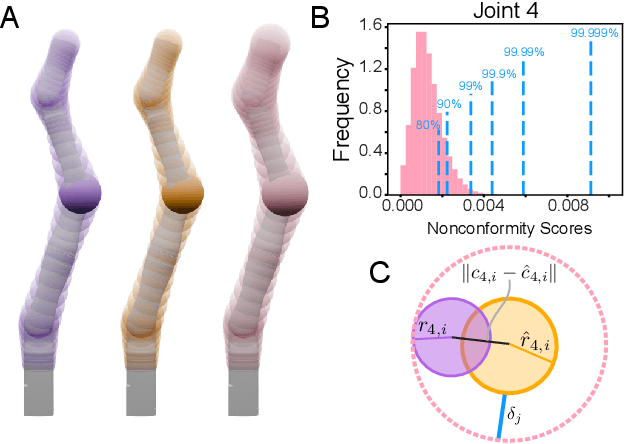
Safe motion planning algorithms are necessary for deploying autonomous robots in unstructured environments. Motion plans must be safe to ensure that the robot does not harm humans or damage any nearby objects. Generating these motion plans in real-time is also important to ensure that the robot can adapt to sudden changes in its environment. Many trajectory optimization methods introduce heuristics that balance safety and real-time performance, potentially increasing the risk of the robot colliding with its environment. This paper addresses this challenge by proposing Conformalized Reachable Sets for Obstacle Avoidance With Spheres (CROWS). CROWS is a novel real-time, receding-horizon trajectory planner that generates probalistically-safe motion plans. Offline, CROWS learns a novel neural network-based representation of a spherebased reachable set that overapproximates the swept volume of the robot's motion. CROWS then uses conformal prediction to compute a confidence bound that provides a probabilistic safety guarantee on the learned reachable set. At runtime, CROWS performs trajectory optimization to select a trajectory that is probabilstically-guaranteed to be collision-free. We demonstrate that CROWS outperforms a variety of state-of-the-art methods in solving challenging motion planning tasks in cluttered environments while remaining collision-free. Code, data, and video demonstrations can be found at https://roahmlab.github.io/crows/

Rapid and Robust Trajectory Optimization for Humanoids

Performing trajectory design for humanoid robots with high degrees of freedom is computationally challenging. The trajectory design process also often involves carefully selecting various hyperparameters and requires a good initial guess which can further complicate the development process. This work introduces a generalized gait optimization framework that directly generates smooth and physically feasible trajectories. The proposed method demonstrates faster and more robust convergence than existing techniques and explicitly incorporates closed-loop kinematic constraints that appear in many modern humanoids. The method is implemented as an open-source C++ codebase which can be found at https://roahmlab.github.io/RAPTOR/.

System Identification For Constrained Robots

Identifying the parameters of robotic systems, such as motor inertia or joint friction, is critical to satisfactory controller synthesis, model analysis, and observer design. Conventional identification techniques are designed primarily for unconstrained systems, such as robotic manipulators. In contrast, the growing importance of legged robots that feature closed kinematic chains or other constraints, poses challenges to these traditional methods. This paper introduces a system identification approach for constrained systems that relies on iterative least squares to identify motor inertia and joint friction parameters from data. The proposed approach is validated in simulation and in the real-world on Digit, which is a 20 degree-of-freedom humanoid robot built by Agility Robotics. In these experiments, the parameters identified by the proposed method enable a model-based controller to achieve better tracking performance than when it uses the default parameters provided by the manufacturer. The implementation of the approach is available at https://github.com/roahmlab/ConstrainedSysID.

Jointed Tails Enhance Control of Three-dimensional Body Rotation

Tails used as inertial appendages induce body rotations of animals and robots, a phenomenon that is governed largely by the ratio of the body and tail moments of inertia. However, vertebrate tails have more degrees of freedom (e.g., number of joints, rotational axes) than most current theoretical models and robotic tails. To understand how morphology affects inertial appendage function, we developed an optimization-based approach that finds the maximally effective tail trajectory and measures error from a target trajectory. For tails of equal total length and mass, increasing the number of equal-length joints increased the complexity of maximally effective tail motions. When we optimized the relative lengths of tail bones while keeping the total tail length, mass, and number of joints the same, this optimization-based approach found that the lengths match the pattern found in the tail bones of mammals specialized for inertial maneuvering. In both experiments, adding joints enhanced the performance of the inertial appendage, but with diminishing returns, largely due to the total control effort constraint. This optimization-based simulation can compare the maximum performance of diverse inertial appendages that dynamically vary in moment of inertia in 3D space, predict inertial capabilities from skeletal data, and inform the design of robotic inertial appendages.

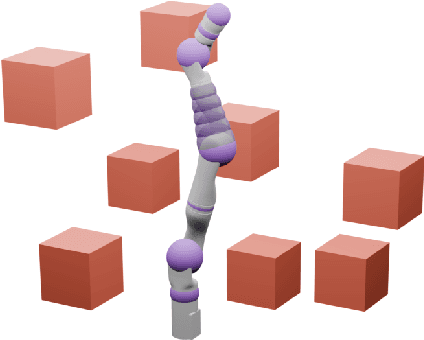
Safe Planning for Articulated Robots Using Reachability-based Obstacle Avoidance With Spheres

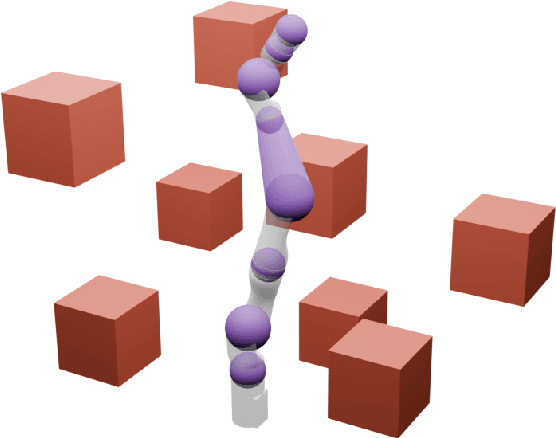
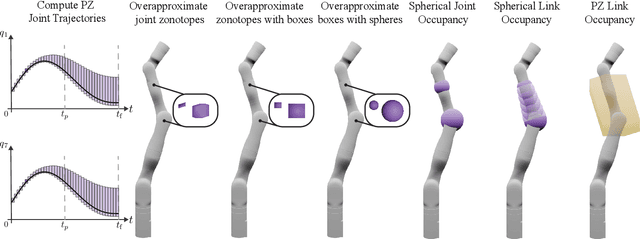
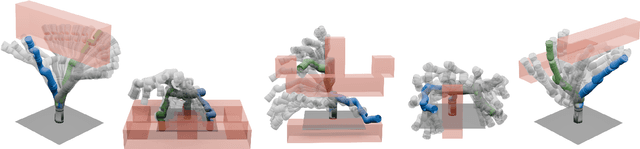
Generating safe motion plans in real-time is necessary for the wide-scale deployment of robots in unstructured and human-centric environments. These motion plans must be safe to ensure humans are not harmed and nearby objects are not damaged. However, they must also be generated in real-time to ensure the robot can quickly adapt to changes in the environment. Many trajectory optimization methods introduce heuristics that trade-off safety and real-time performance, which can lead to potentially unsafe plans. This paper addresses this challenge by proposing Safe Planning for Articulated Robots Using Reachability-based Obstacle Avoidance With Spheres (SPARROWS). SPARROWS is a receding-horizon trajectory planner that utilizes the combination of a novel reachable set representation and an exact signed distance function to generate provably-safe motion plans. At runtime, SPARROWS uses parameterized trajectories to compute reachable sets composed entirely of spheres that overapproximate the swept volume of the robot's motion. SPARROWS then performs trajectory optimization to select a safe trajectory that is guaranteed to be collision-free. We demonstrate that SPARROWS' novel reachable set is significantly less conservative than previous approaches. We also demonstrate that SPARROWS outperforms a variety of state-of-the-art methods in solving challenging motion planning tasks in cluttered environments. Code, data, and video demonstrations can be found at \url{https://roahmlab.github.io/sparrows/}.

Serving Time: Real-Time, Safe Motion Planning and Control for Manipulation of Unsecured Objects

A key challenge to ensuring the rapid transition of robotic systems from the industrial sector to more ubiquitous applications is the development of algorithms that can guarantee safe operation while in close proximity to humans. Motion planning and control methods, for instance, must be able to certify safety while operating in real-time in arbitrary environments and in the presence of model uncertainty. This paper proposes Wrench Analysis for Inertial Transport using Reachability (WAITR), a certifiably safe motion planning and control framework for serial link manipulators that manipulate unsecured objects in arbitrary environments. WAITR uses reachability analysis to construct over-approximations of the contact wrench applied to unsecured objects, which captures uncertainty in the manipulator dynamics, the object dynamics, and contact parameters such as the coefficient of friction. An optimization problem formulation is presented that can be solved in real-time to generate provably-safe motions for manipulating the unsecured objects. This paper illustrates that WAITR outperforms state of the art methods in a variety of simulation experiments and demonstrates its performance in the real-world.