Data Skeleton Learning: Scalable Active Clustering with Sparse Graph Structures

In this work, we focus on the efficiency and scalability of pairwise constraint-based active clustering, crucial for processing large-scale data in applications such as data mining, knowledge annotation, and AI model pre-training. Our goals are threefold: (1) to reduce computational costs for iterative clustering updates; (2) to enhance the impact of user-provided constraints to minimize annotation requirements for precise clustering; and (3) to cut down memory usage in practical deployments. To achieve these aims, we propose a graph-based active clustering algorithm that utilizes two sparse graphs: one for representing relationships between data (our proposed data skeleton) and another for updating this data skeleton. These two graphs work in concert, enabling the refinement of connected subgraphs within the data skeleton to create nested clusters. Our empirical analysis confirms that the proposed algorithm consistently facilitates more accurate clustering with dramatically less input of user-provided constraints, and outperforms its counterparts in terms of computational performance and scalability, while maintaining robustness across various distance metrics.

Jointed Tails Enhance Control of Three-dimensional Body Rotation

Tails used as inertial appendages induce body rotations of animals and robots, a phenomenon that is governed largely by the ratio of the body and tail moments of inertia. However, vertebrate tails have more degrees of freedom (e.g., number of joints, rotational axes) than most current theoretical models and robotic tails. To understand how morphology affects inertial appendage function, we developed an optimization-based approach that finds the maximally effective tail trajectory and measures error from a target trajectory. For tails of equal total length and mass, increasing the number of equal-length joints increased the complexity of maximally effective tail motions. When we optimized the relative lengths of tail bones while keeping the total tail length, mass, and number of joints the same, this optimization-based approach found that the lengths match the pattern found in the tail bones of mammals specialized for inertial maneuvering. In both experiments, adding joints enhanced the performance of the inertial appendage, but with diminishing returns, largely due to the total control effort constraint. This optimization-based simulation can compare the maximum performance of diverse inertial appendages that dynamically vary in moment of inertia in 3D space, predict inertial capabilities from skeletal data, and inform the design of robotic inertial appendages.

Advantages of Bilinear Koopman Realizations for the Modeling and Control of Systems with Unknown Dynamics

Nonlinear dynamical systems can be made easier to control by lifting them into the space of observable functions, where their evolution is described by the linear Koopman operator. This paper describes how the Koopman operator can be used to generate approximate linear, bilinear, and nonlinear model realizations from data, and argues in favor of bilinear realizations for characterizing systems with unknown dynamics. Necessary and sufficient conditions for a dynamical system to have a valid linear or bilinear realization over a given set of observable functions are presented and used to show that every control-affine system admits an infinite-dimensional bilinear realization, but does not necessarily admit a linear one. Therefore, approximate bilinear realizations constructed from generic sets of basis functions tend to improve as the number of basis functions increases, whereas approximate linear realizations may not. To demonstrate the advantages of bilinear Koopman realizations for control, a linear, bilinear, and nonlinear Koopman model realization of a simulated robot arm are constructed from data. In a trajectory following task, the bilinear realization exceeds the prediction accuracy of the linear realization and the computational efficiency of the nonlinear realization when incorporated into a model predictive control framework.

Koopman-based Control of a Soft Continuum Manipulator Under Variable Loading Conditions

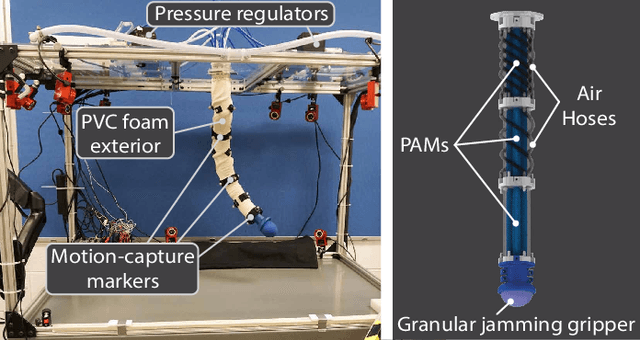
Controlling soft continuum manipulator arms is difficult due to their infinite degrees of freedom, nonlinear material properties, and large deflections under loading. This paper presents a data-driven approach to identifying soft manipulator models that enables consistent control under variable loading conditions. This is achieved by incorporating loads into a linear Koopman operator model as states and estimating their values online via an observer within the control loop. Using this approach, real-time, fully autonomous control of a pneumatically actuated soft continuum manipulator is achieved. In several trajectory following experiments, this controller is shown to be more accurate and precise than controllers based on models that are unable to explicitly account for loading. The manipulator also successfully performs pick and place of objects with unknown mass, demonstrating the efficacy of this approach in executing real-world manipulation tasks.