C. David Remy
Impact of Leg Stiffness on Energy Efficiency in One Legged Hopping
Jan 07, 2025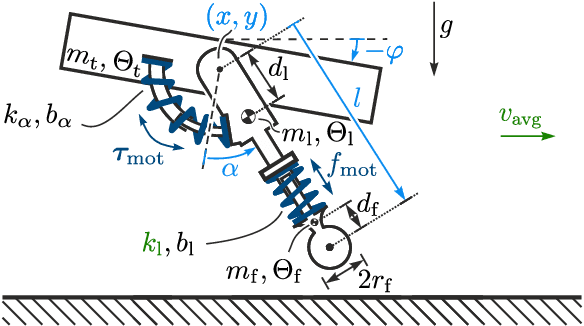
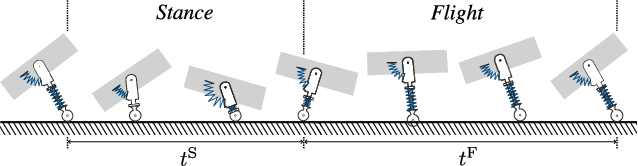
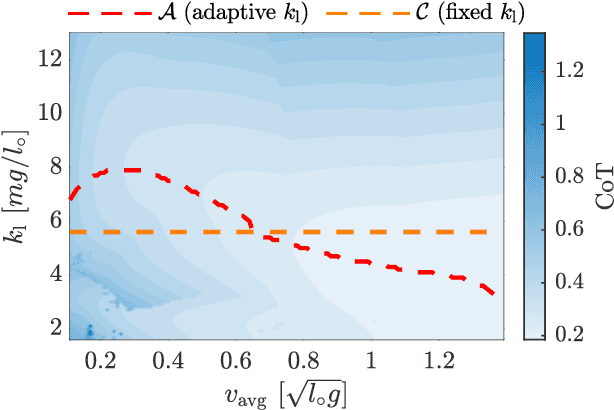
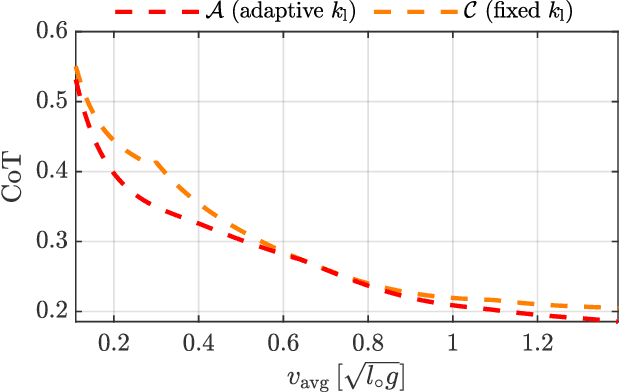
Abstract:In the fields of robotics and biomechanics, the integration of elastic elements such as springs and tendons in legged systems has long been recognized for enabling energy-efficient locomotion. Yet, a significant challenge persists: designing a robotic leg that perform consistently across diverse operating conditions, especially varying average forward speeds. It remains unclear whether, for such a range of operating conditions, the stiffness of the elastic elements needs to be varied or if a similar performance can be obtained by changing the motion and actuation while keeping the stiffness fixed. This work explores the influence of the leg stiffness on the energy efficiency of a monopedal robot through an extensive parametric study of its periodic hopping motion. To this end, we formulate an optimal control problem parameterized by average forward speed and leg stiffness, solving it numerically using direct collocation. Our findings indicate that, compared to the use of a fixed stiffness, employing variable stiffness in legged systems improves energy efficiency by 20 % maximally and by 6.8 % on average across a range of speeds.
The impact of AI on engineering design procedures for dynamical systems
Dec 16, 2024Abstract:Artificial intelligence (AI) is driving transformative changes across numerous fields, revolutionizing conventional processes and creating new opportunities for innovation. The development of mechatronic systems is undergoing a similar transformation. Over the past decade, modeling, simulation, and optimization techniques have become integral to the design process, paving the way for the adoption of AI-based methods. In this paper, we examine the potential for integrating AI into the engineering design process, using the V-model from the VDI guideline 2206, considered the state-of-the-art in product design, as a foundation. We identify and classify AI methods based on their suitability for specific stages within the engineering product design workflow. Furthermore, we present a series of application examples where AI-assisted design has been successfully implemented by the authors. These examples, drawn from research projects within the DFG Priority Program \emph{SPP~2353: Daring More Intelligence - Design Assistants in Mechanics and Dynamics}, showcase a diverse range of applications across mechanics and mechatronics, including areas such as acoustics and robotics.
Bipedal walking with continuously compliant robotic legs
Nov 11, 2024
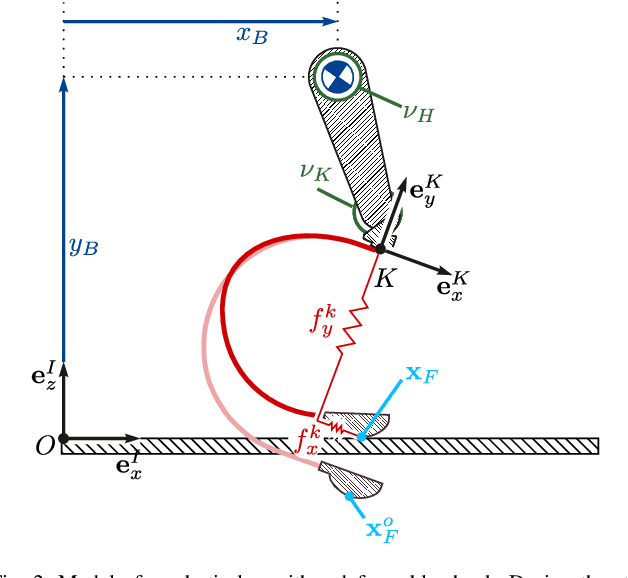
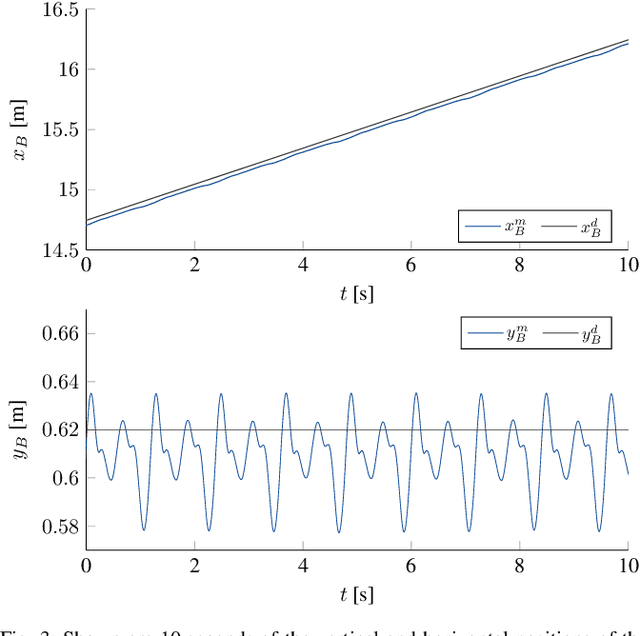

Abstract:In biomechanics and robotics, elasticity plays a crucial role in enhancing locomotion efficiency and stability. Traditional approaches in legged robots often employ series elastic actuators (SEA) with discrete rigid components, which, while effective, add weight and complexity. This paper presents an innovative alternative by integrating continuously compliant structures into the lower legs of a bipedal robot, fundamentally transforming the SEA concept. Our approach replaces traditional rigid segments with lightweight, deformable materials, reducing overall mass and simplifying the actuation design. This novel design introduces unique challenges in modeling, sensing, and control, due to the infinite dimensionality of continuously compliant elements. We address these challenges through effective approximations and control strategies. The paper details the design and modeling of the compliant leg structure, presents low-level force and kinematics controllers, and introduces a high-level posture controller with a gait scheduler. Experimental results demonstrate successful bipedal walking using this new design.
The Indirect Method for Generating Libraries of Optimal Periodic Trajectories and Its Application to Economical Bipedal Walking
Oct 12, 2024Abstract:Trajectory optimization is an essential tool for generating efficient and dynamically consistent gaits in legged locomotion. This paper explores the indirect method of trajectory optimization, emphasizing its application in creating optimal periodic gaits for legged systems and contrasting it with the more commonly used direct method. While the direct method provides considerable flexibility in its implementation, it is limited by its input space parameterization. In contrast, the indirect method improves accuracy by defining control inputs as functions of the system's states and costates. We tackle the convergence challenges associated with indirect shooting methods, particularly through the systematic development of gait libraries by utilizing numerical continuation methods. Our contributions include: (1) the formalization of a general periodic trajectory optimization problem that extends existing first-order necessary conditions for a broader range of cost functions and operating conditions; (2) a methodology for efficiently generating libraries of optimal trajectories (gaits) utilizing a single shooting approach combined with numerical continuation methods, including a novel approach for reconstructing Lagrange multipliers and costates from passive gaits; and (3) a comparative analysis of the indirect and direct shooting methods using a compass-gait walker as a case study, demonstrating the former's superior accuracy in generating optimal gaits. The findings underscore the potential of the indirect method for generating families of optimal gaits, thereby advancing the field of trajectory optimization in legged robotics.
Swing-Up of a Weakly Actuated Double Pendulum via Nonlinear Normal Modes
Apr 12, 2024



Abstract:We identify the nonlinear normal modes spawning from the stable equilibrium of a double pendulum under gravity, and we establish their connection to homoclinic orbits through the unstable upright position as energy increases. This result is exploited to devise an efficient swing-up strategy for a double pendulum with weak, saturating actuators. Our approach involves stabilizing the system onto periodic orbits associated with the nonlinear modes while gradually injecting energy. Since these modes are autonomous system evolutions, the required control effort for stabilization is minimal. Even with actuator limitations of less than 1% of the maximum gravitational torque, the proposed method accomplishes the swing-up of the double pendulum by allowing sufficient time.
An Approach for Generating Families of Energetically Optimal Gaits from Passive Dynamic Walking Gaits
Mar 26, 2023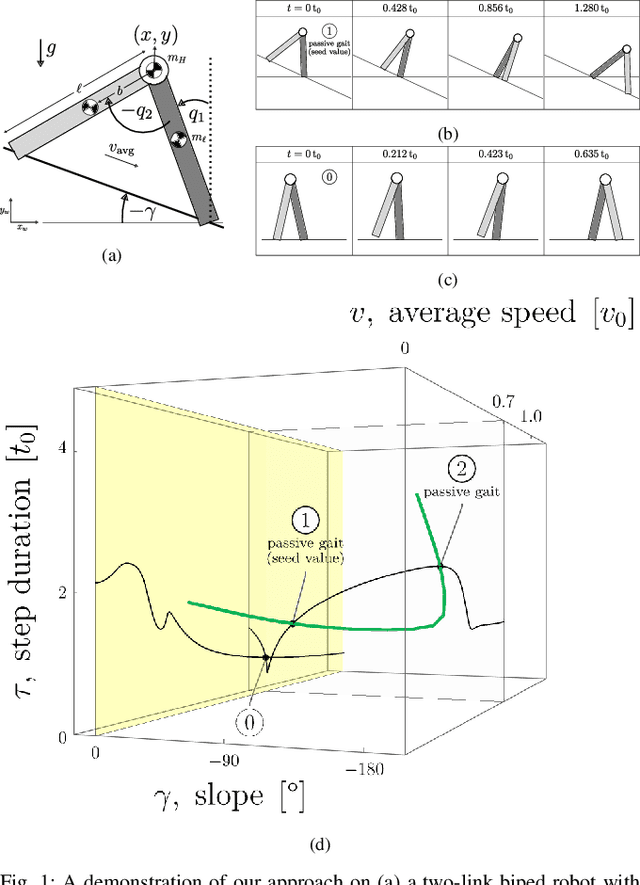
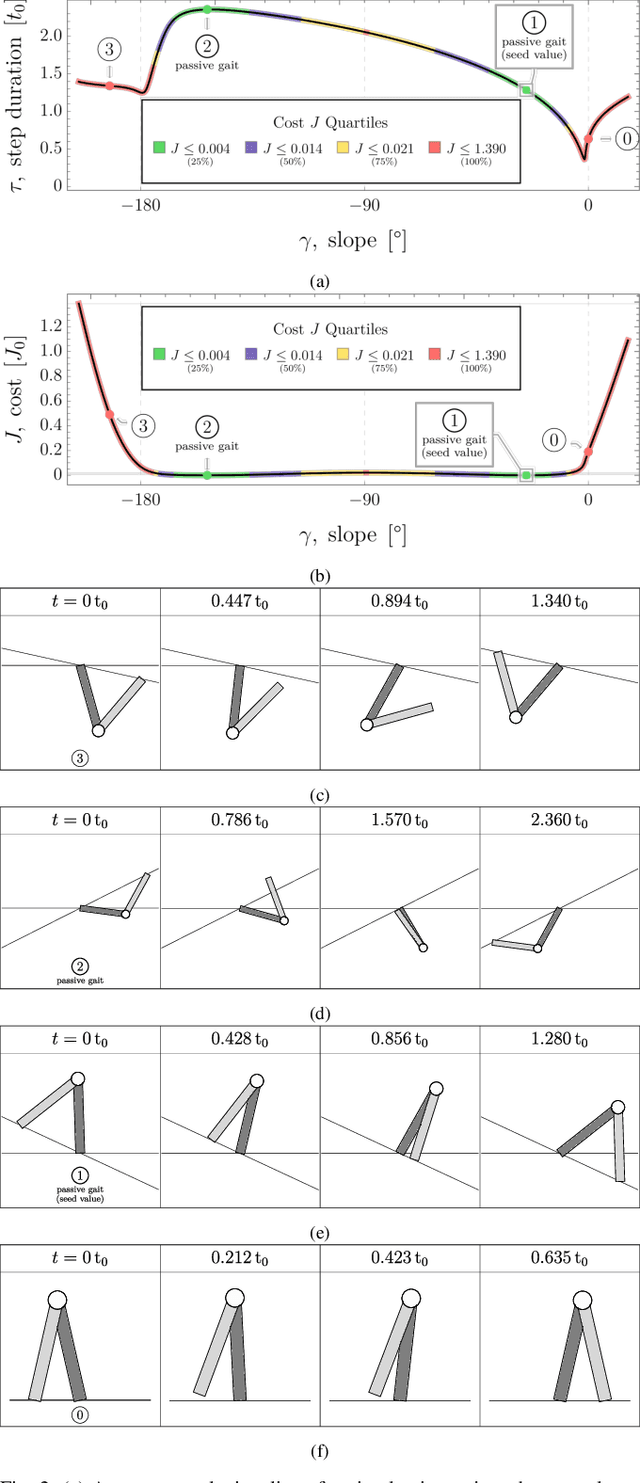
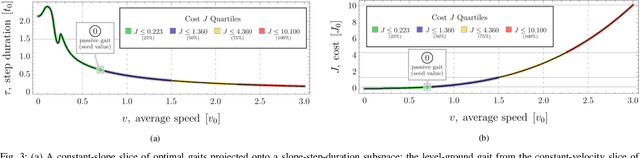
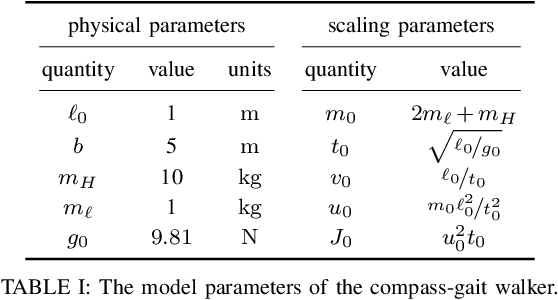
Abstract:For a class of biped robots with impulsive dynamics and a non-empty set of passive gaits (unactuated, periodic motions of the biped model), we present a method for computing continuous families of locally optimal gaits with respect to a class of commonly used energetic cost functions (e.g., the integral of torque-squared). We compute these families using only the passive gaits of the biped, which are globally optimal gaits with respect to these cost functions. Our approach fills in an important gap in the literature when computing a library of locally optimal gaits, which often do not make use of these globally optimal solutions as seed values. We demonstrate our approach on a well-studied two-link biped model.
Connecting Gaits in Energetically Conservative Legged Systems
Feb 25, 2022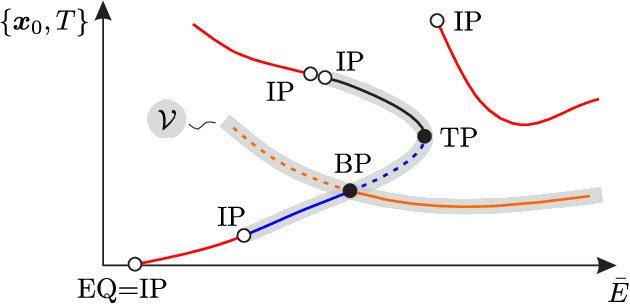
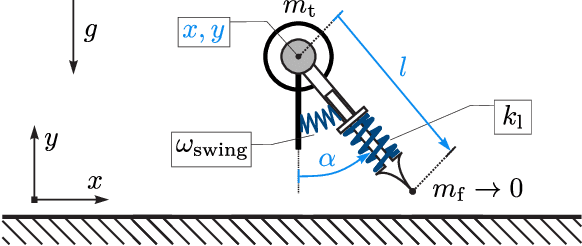
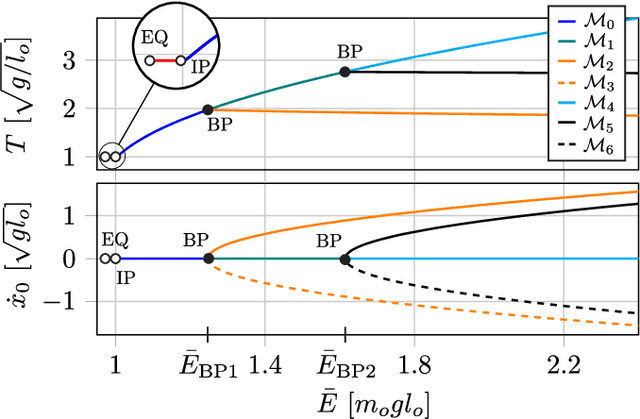
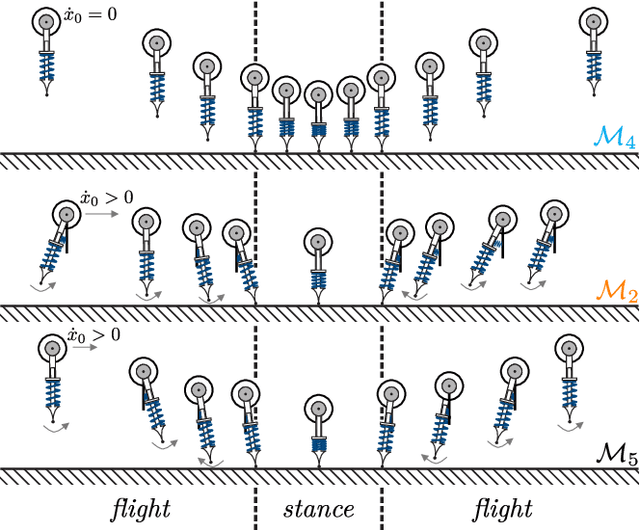
Abstract:In this work, we present a nonlinear dynamics perspective on generating and connecting gaits for energetically conservative models of legged systems. In particular, we show that the set of conservative gaits constitutes a connected space of locally defined 1D submanifolds in the gait space. These manifolds are coordinate-free parameterized by energy level. We present algorithms for identifying such families of gaits through the use of numerical continuation methods, generating sets and bifurcation points. To this end, we also introduce several details for the numerical implementation. Most importantly, we establish the necessary condition for the Delassus' matrix to preserve energy across impacts. An important application of our work is with simple models of legged locomotion that are often able to capture the complexity of legged locomotion with just a few degrees of freedom and a small number of physical parameters. We demonstrate the efficacy of our framework on a one-legged hopper with four degrees of freedom.
Design and Control of a Recovery System for Legged Robots
Nov 29, 2021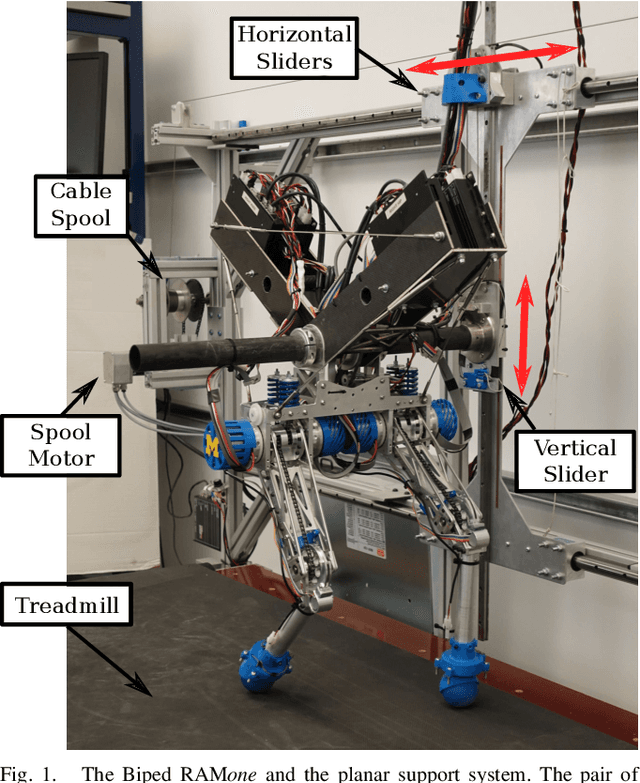



Abstract:This paper describes the design and control of a support and recovery system for use with planar legged robots. The system operates in three modes. First, it can be operated in a fully transparent mode where no forces are applied to the robot. In this mode, the system follows the robot closely to be able to quickly catch the robot if needed. Second, it can provide a vertical supportive force to assist a robot during operation. Third, it can catch the robot and pull it away from the ground after a failure to avoid falls and the associated damages. In this mode, the system automatically resets the robot after a trial allowing for multiple consecutive trials to be run without manual intervention. The supportive forces are applied to the robot through an actuated cable and pulley system that uses series elastic actuation with a unidirectional spring to enable truly transparent operation. The nonlinear nature of this system necessitates careful design of controllers to ensure predictable, safe behaviors. In this paper we introduce the mechatronic design of the recovery system, develop suitable controllers, and evaluate the system's performance on the bipedal robot RAMone.
Koopman-based Control of a Soft Continuum Manipulator Under Variable Loading Conditions
Feb 04, 2020
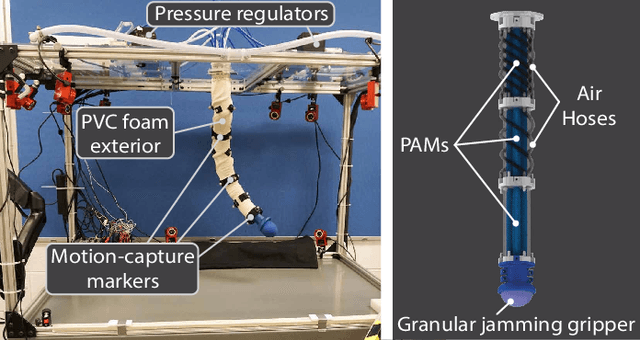


Abstract:Controlling soft continuum manipulator arms is difficult due to their infinite degrees of freedom, nonlinear material properties, and large deflections under loading. This paper presents a data-driven approach to identifying soft manipulator models that enables consistent control under variable loading conditions. This is achieved by incorporating loads into a linear Koopman operator model as states and estimating their values online via an observer within the control loop. Using this approach, real-time, fully autonomous control of a pneumatically actuated soft continuum manipulator is achieved. In several trajectory following experiments, this controller is shown to be more accurate and precise than controllers based on models that are unable to explicitly account for loading. The manipulator also successfully performs pick and place of objects with unknown mass, demonstrating the efficacy of this approach in executing real-world manipulation tasks.
Walking with Confidence: Safety Regulation for Full Order Biped Models
Mar 20, 2019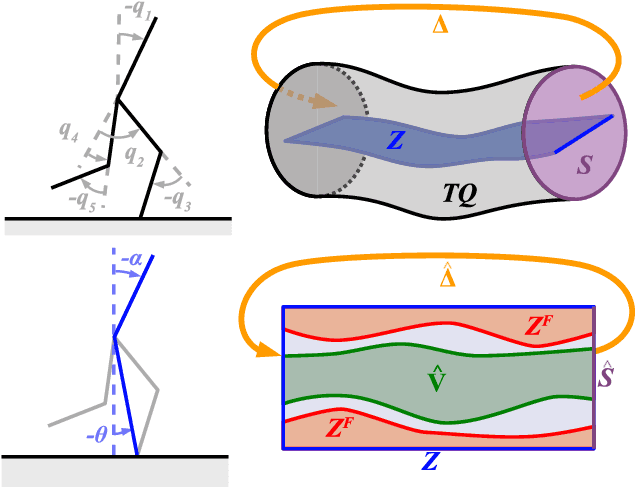
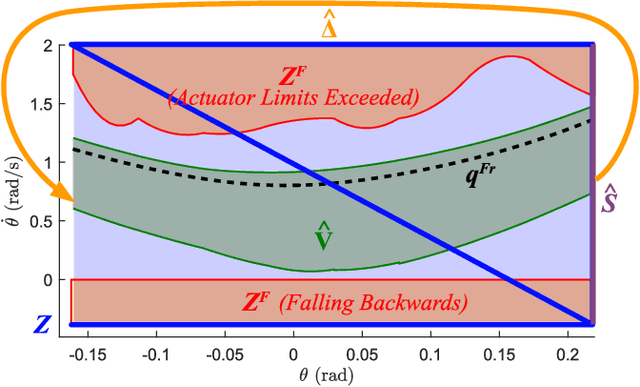
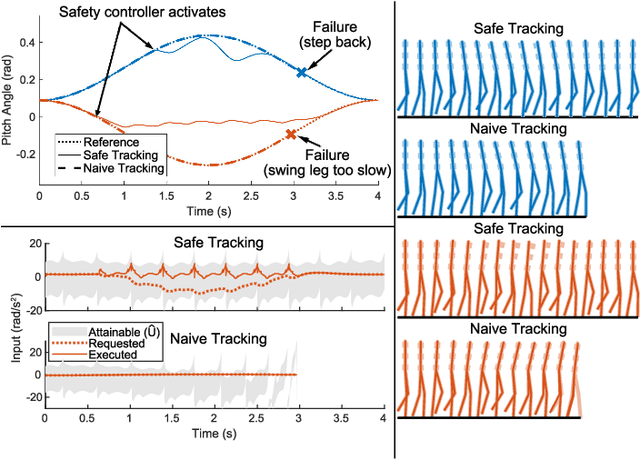
Abstract:Safety guarantees are valuable in the control of walking robots, as falling can be both dangerous and costly. Unfortunately, set-based tools for generating safety guarantees (such as sums-of-squares optimization) are typically restricted to simplified, low-dimensional models of walking robots. For more complex models, methods based on hybrid zero dynamics can ensure the local stability of a pre-specified limit cycle, but provide limited guarantees. This paper combines the benefits of both approaches by using sums-of-squares optimization on a hybrid zero dynamics manifold to generate a guaranteed safe set for a 10-dimensional walking robot model. Along with this set, this paper describes how to generate a controller that maintains safety by modifying the manifold parameters when on the edge of the safe set. The proposed approach, which is applied to a bipedal Rabbit model, provides a roadmap for applying sums-of-squares verification techniques to high dimensional systems. This opens the door for a broad set of tools that can generate safety guarantees and regulating controllers for complex walking robot models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge