An Approach for Generating Families of Energetically Optimal Gaits from Passive Dynamic Walking Gaits
Paper and Code
Mar 26, 2023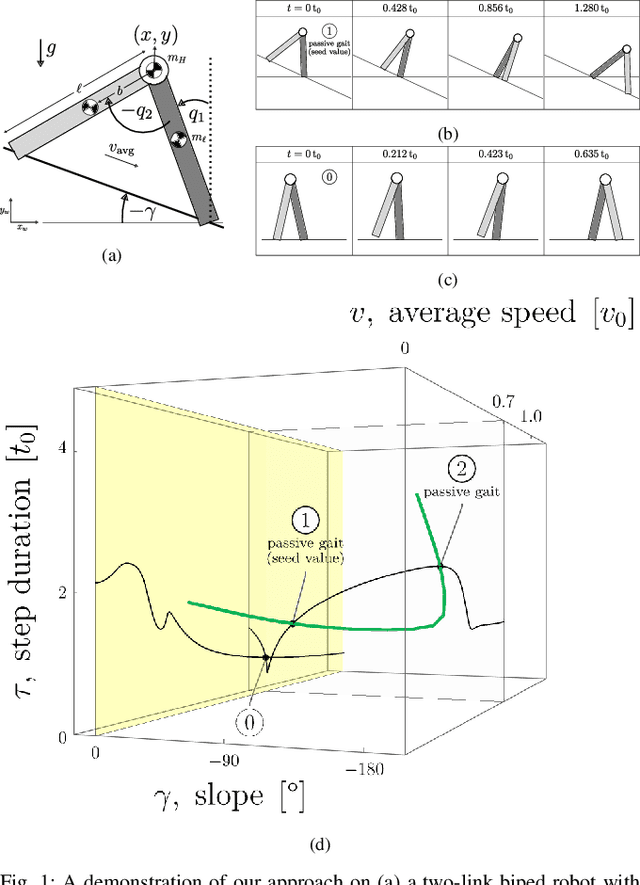
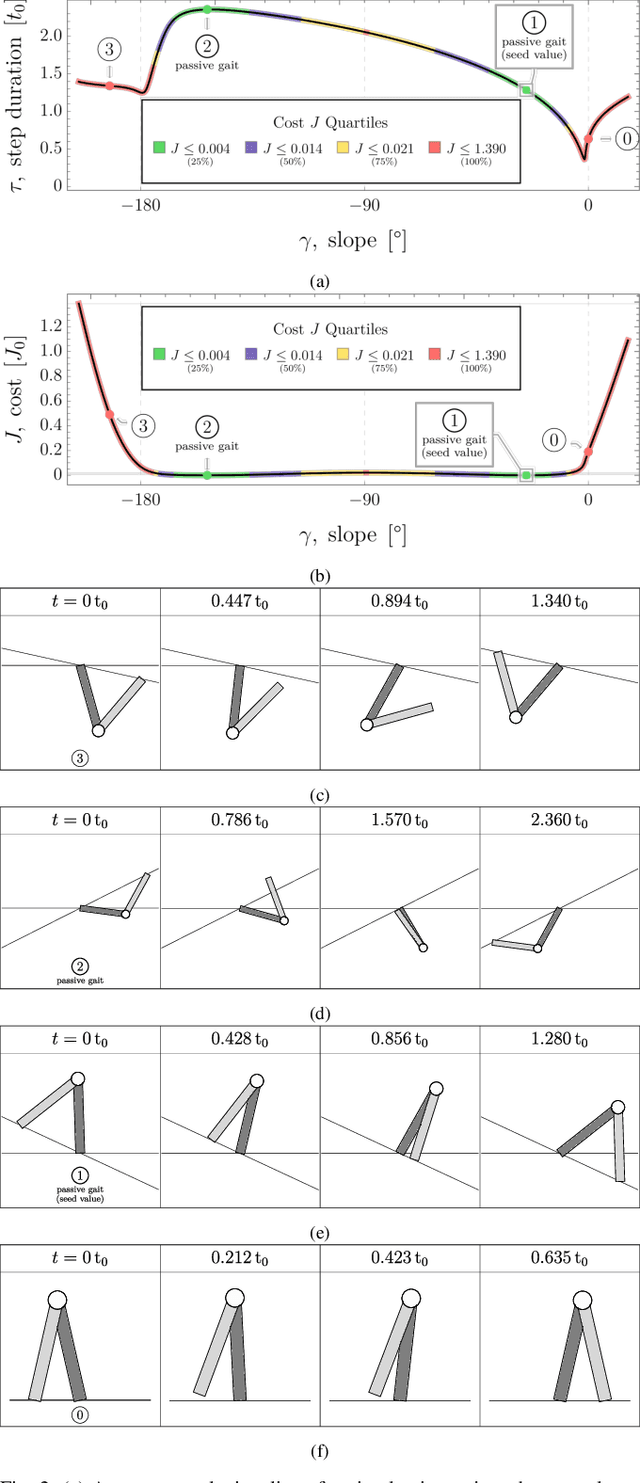
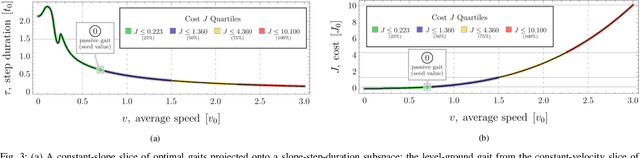
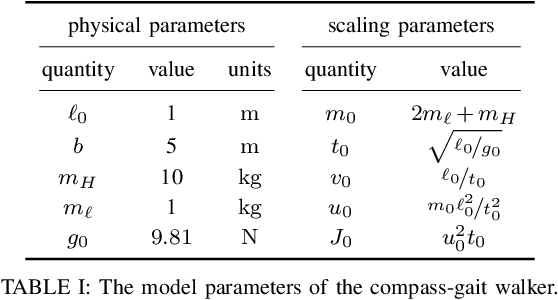
For a class of biped robots with impulsive dynamics and a non-empty set of passive gaits (unactuated, periodic motions of the biped model), we present a method for computing continuous families of locally optimal gaits with respect to a class of commonly used energetic cost functions (e.g., the integral of torque-squared). We compute these families using only the passive gaits of the biped, which are globally optimal gaits with respect to these cost functions. Our approach fills in an important gap in the literature when computing a library of locally optimal gaits, which often do not make use of these globally optimal solutions as seed values. We demonstrate our approach on a well-studied two-link biped model.
* Code available, see
https://github.com/nr-codes/OptimalGaitsForCompassGait
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge