Connecting Gaits in Energetically Conservative Legged Systems

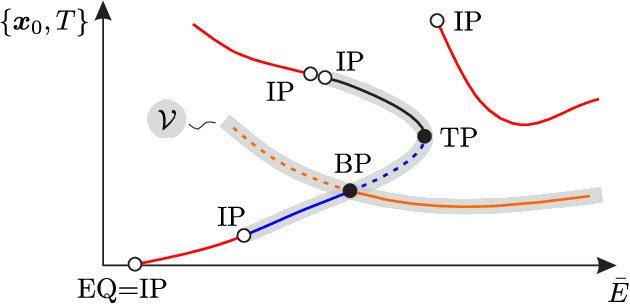
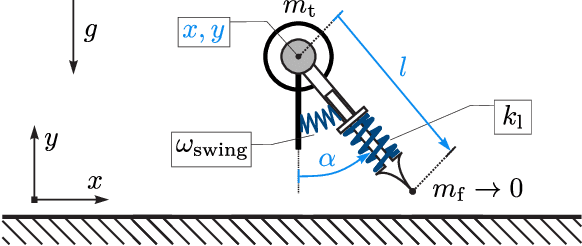
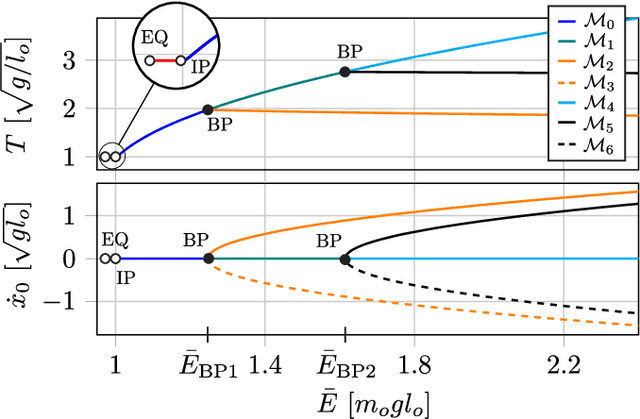
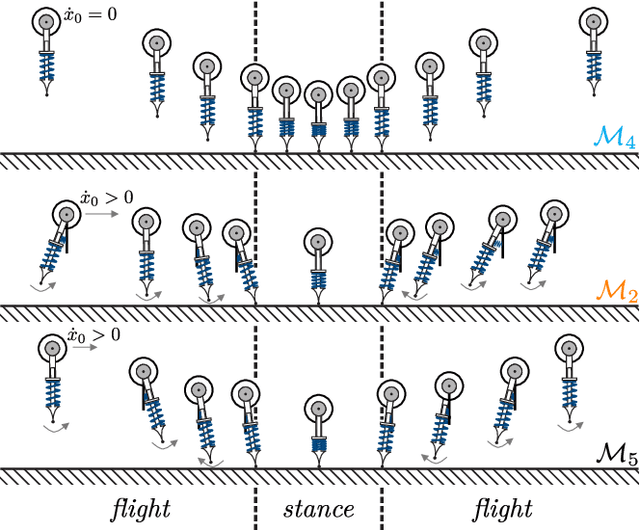
In this work, we present a nonlinear dynamics perspective on generating and connecting gaits for energetically conservative models of legged systems. In particular, we show that the set of conservative gaits constitutes a connected space of locally defined 1D submanifolds in the gait space. These manifolds are coordinate-free parameterized by energy level. We present algorithms for identifying such families of gaits through the use of numerical continuation methods, generating sets and bifurcation points. To this end, we also introduce several details for the numerical implementation. Most importantly, we establish the necessary condition for the Delassus' matrix to preserve energy across impacts. An important application of our work is with simple models of legged locomotion that are often able to capture the complexity of legged locomotion with just a few degrees of freedom and a small number of physical parameters. We demonstrate the efficacy of our framework on a one-legged hopper with four degrees of freedom.

A Topological Approach to Gait Generation for Biped Robots

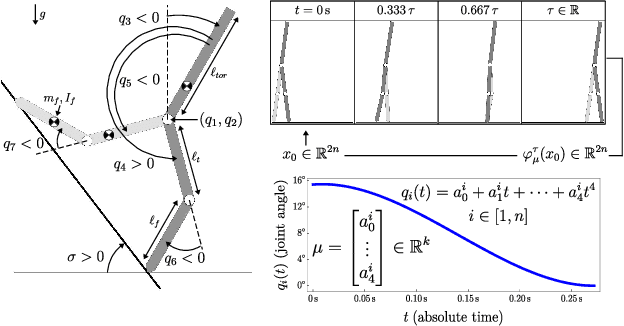
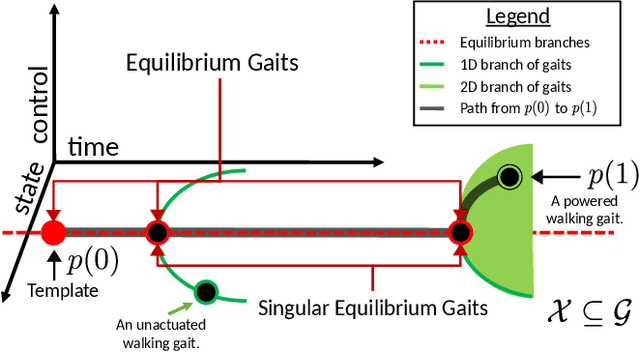
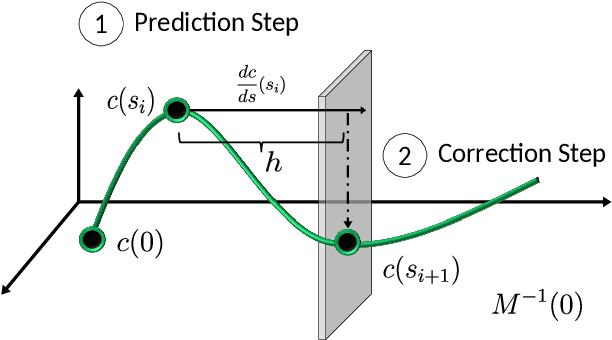
This paper describes a topological approach to generating families of open- and closed-loop walking gaits for underactuated 2D and 3D biped walkers subject to configuration inequality constraints, physical holonomic constraints (e.g., closed chains), and virtual holonomic constraints (user-defined constraints enforced through feedback control). Our method constructs implicitly-defined manifolds of feasible periodic gaits within a state-time-control space that parameterizes the biped's hybrid trajectories. Since equilibrium configurations of the biped often belong to such manifolds, we use equilibria as "templates" from which to grow the gait families. Equilibria are reliable seeds for the construction of gait families, eliminating the need for random, intuited, or bio-inspired initial guesses at feasible trajectories in an optimization framework. We demonstrate the approach on several 2D and 3D biped walkers.