A Topological Approach to Gait Generation for Biped Robots

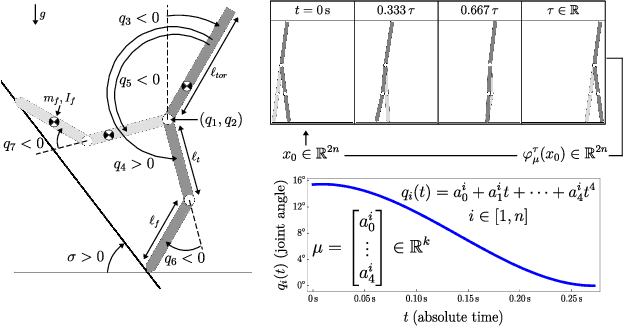
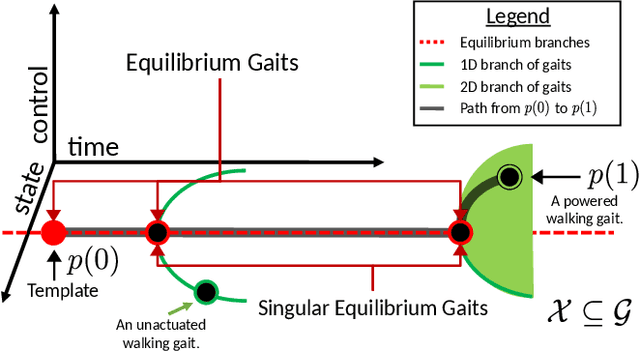
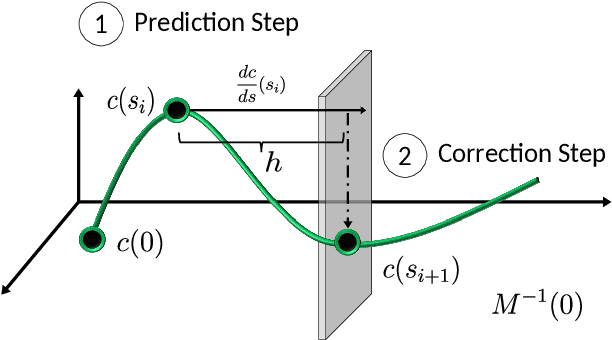
This paper describes a topological approach to generating families of open- and closed-loop walking gaits for underactuated 2D and 3D biped walkers subject to configuration inequality constraints, physical holonomic constraints (e.g., closed chains), and virtual holonomic constraints (user-defined constraints enforced through feedback control). Our method constructs implicitly-defined manifolds of feasible periodic gaits within a state-time-control space that parameterizes the biped's hybrid trajectories. Since equilibrium configurations of the biped often belong to such manifolds, we use equilibria as "templates" from which to grow the gait families. Equilibria are reliable seeds for the construction of gait families, eliminating the need for random, intuited, or bio-inspired initial guesses at feasible trajectories in an optimization framework. We demonstrate the approach on several 2D and 3D biped walkers.