Swing-Up of a Weakly Actuated Double Pendulum via Nonlinear Normal Modes

We identify the nonlinear normal modes spawning from the stable equilibrium of a double pendulum under gravity, and we establish their connection to homoclinic orbits through the unstable upright position as energy increases. This result is exploited to devise an efficient swing-up strategy for a double pendulum with weak, saturating actuators. Our approach involves stabilizing the system onto periodic orbits associated with the nonlinear modes while gradually injecting energy. Since these modes are autonomous system evolutions, the required control effort for stabilization is minimal. Even with actuator limitations of less than 1% of the maximum gravitational torque, the proposed method accomplishes the swing-up of the double pendulum by allowing sufficient time.

EigenMPC: An Eigenmanifold-Inspired Model-Predictive Control Framework for Exciting Efficient Oscillations in Mechanical Systems

This paper proposes a Nonlinear Model-Predictive Control (NMPC) method capable of finding and converging to energy-efficient regular oscillations, which require no control action to be sustained. The approach builds up on the recently developed Eigenmanifold theory, which defines the sets of line-shaped oscillations of a robot as an invariant two-dimensional submanifold of its state space. By defining the control problem as a nonlinear program (NLP), the controller is able to deal with constraints in the state and control variables and be energy-efficient not only in its final trajectory but also during the convergence phase. An initial implementation of this approach is proposed, analyzed, and tested in simulation.

What Can Algebraic Topology and Differential Geometry Teach Us About Intrinsic Dynamics and Global Behavior of Robots?

Traditionally, robots are regarded as universal motion generation machines. They are designed mainly by kinematics considerations while the desired dynamics is imposed by strong actuators and high-rate control loops. As an alternative, one can first consider the robot's intrinsic dynamics and optimize it in accordance with the desired tasks. Therefore, one needs to better understand intrinsic, uncontrolled dynamics of robotic systems. In this paper we focus on periodic orbits, as fundamental dynamic properties with many practical applications. Algebraic topology and differential geometry provide some fundamental statements about existence of periodic orbits. As an example, we present periodic orbits of the simplest multi-body system: the double-pendulum in gravity. This simple system already displays a rich variety of periodic orbits. We classify these into three classes: toroidal orbits, disk orbits and nonlinear normal modes. Some of these we found by geometrical insights and some by numerical simulation and sampling.

Quasi-Orthogonal Foliations of the Configuration Space -- A Redundancy Resolution Approach at Position Level

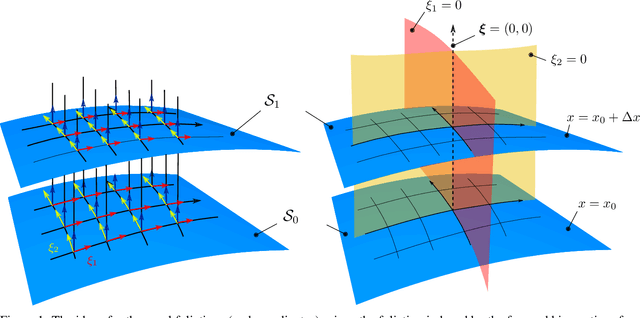
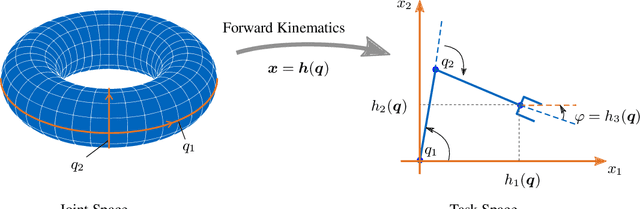
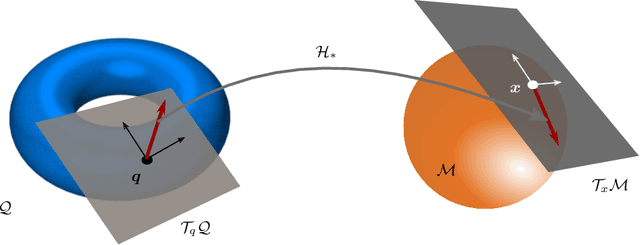
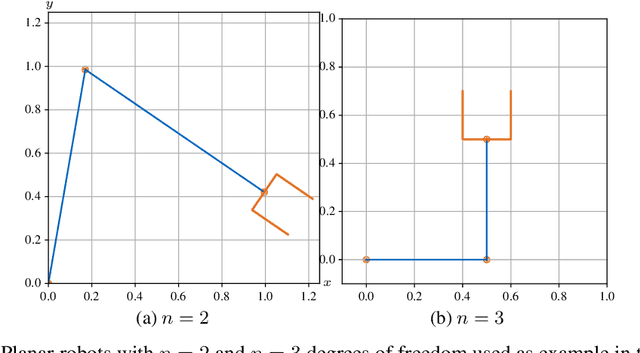
High versatility and flexibility of robotic systems require kinematic structures with many degrees of freedom. This usually renders the system kinematically redundant, i.e., its maneuvers are not fully determined by the main manipulation or interaction task. Additional constraints or objectives are required to solve the under-determined control and planning problems. The state-of-the-art approaches involve arranging tasks in a hierarchy and decoupling lower from higher priority tasks on velocity or torque level. Velocities and torques are elements of vector and covector spaces, respectively, and thus the approaches are inherently based on linear algebra tools. In this paper, we develop an approach to redundancy resolution and decoupling on position level. That requires moving from vector spaces and linear algebra to manifolds and differential geometry. We propose to determine, in addition to the task forward kinematics, another set of coordinate functions. The Jacobian of those functions shall resemble the conditions known from the linear algebra-based velocity- and torque-level decoupling to the best extent possible. The approach provides a better insight into the topological properties of robot kinematics and control problems, allowing a more global geometrical view. Quasi-decoupled coordinates can help to avoid or diminish some practical and theoretical difficulties related to the classical projection approaches at the cost of higher offline computational efforts. A condition for the existence of these coordinates is derived. If the condition is not satisfied, one can still find approximate solutions by numerical optimization. Finally, we show simulation results for both, trajectory tracking and classical impedance control.