Quasi-Orthogonal Foliations of the Configuration Space -- A Redundancy Resolution Approach at Position Level

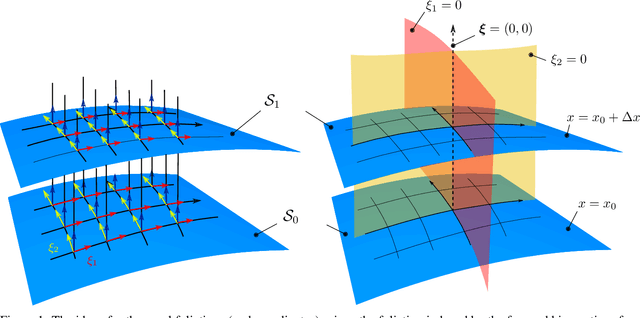
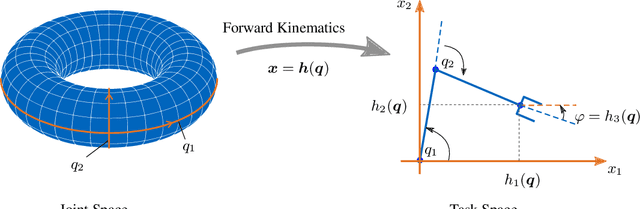
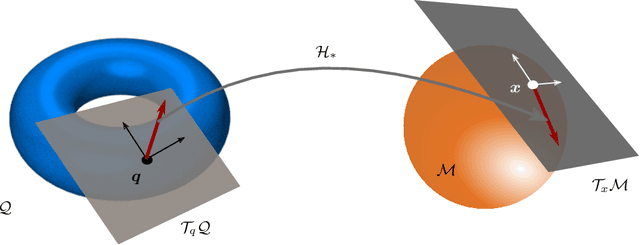
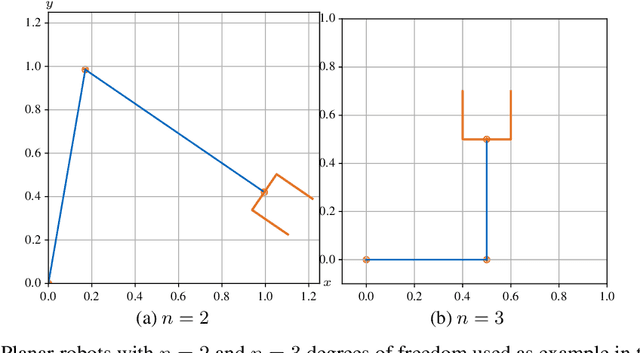
High versatility and flexibility of robotic systems require kinematic structures with many degrees of freedom. This usually renders the system kinematically redundant, i.e., its maneuvers are not fully determined by the main manipulation or interaction task. Additional constraints or objectives are required to solve the under-determined control and planning problems. The state-of-the-art approaches involve arranging tasks in a hierarchy and decoupling lower from higher priority tasks on velocity or torque level. Velocities and torques are elements of vector and covector spaces, respectively, and thus the approaches are inherently based on linear algebra tools. In this paper, we develop an approach to redundancy resolution and decoupling on position level. That requires moving from vector spaces and linear algebra to manifolds and differential geometry. We propose to determine, in addition to the task forward kinematics, another set of coordinate functions. The Jacobian of those functions shall resemble the conditions known from the linear algebra-based velocity- and torque-level decoupling to the best extent possible. The approach provides a better insight into the topological properties of robot kinematics and control problems, allowing a more global geometrical view. Quasi-decoupled coordinates can help to avoid or diminish some practical and theoretical difficulties related to the classical projection approaches at the cost of higher offline computational efforts. A condition for the existence of these coordinates is derived. If the condition is not satisfied, one can still find approximate solutions by numerical optimization. Finally, we show simulation results for both, trajectory tracking and classical impedance control.